
マンデルブロ集合の外側を滑らかに彩色する
どうも、108Hassiumです。
以前、こんな記事を書きました。
この記事ではマンデルブロ集合の描画方法をざっくりと解説し、汎用性の高い彩色関数として以下のものを紹介しました。
fill(cr(n*7),cr(n*8),cr(n*9));これを使って描画したマンデルブロ集合は以下のようになります。

この画像では、マンデルブロ集合の外側の色は不連続的に変化し、場所によっては変化が急すぎて色の境目が目立ってしまっているところもあります。
また、極端な例として以下のようなものもあります。
fill(cr(c*99),cr(c*99+85),cr(c*99+170));
これは色の境界がかなりはっきりと分かれてしまっています。
しかし、最近このような彩色法を改良して境界の部分を滑らかにする方法を見つけたので紹介したいと思います。
コード&サンプル
まず、ソースコードがこちらです。(言語はProcessing)
void setup(){
size(2000,2000);
background(0);
noStroke();
double x,y,px,py,a,b;
float f;
boolean o;
for(int k=0;k<2000;k++){
for(int m=0;m<2000;m++){
a=(double)k/500.0-2.0;
b=(double)m/500.0-2.0;
x=0;
y=0;
o=true;
for(int n=1;n<=500&&o;n++){
px=x;
py=y;
x=px*px-py*py+a;
y=2.0*px*py+b;
if(x*x+y*y>4){
o=false;
f=(float)((4.0-px*px-py*py)/(x*x+y*y-px*px-py*py));
fill(cr((n+f)*7),cr((n+f)*8),cr((n+f)*9));
rect(k,m,1,1);
}
}
}
}
}
float cr(float n){
return (n%256)*(256-(n%256))/65;
}実行結果はこうなります。

冒頭の画像と比べると、少し滑らかになったような気がします。
所々に見える境界線の跡みたいなのが気になる場合は、fに代入する式を以下のように書き換えてください。
f=(float)((4.0-px*px-py*py)/(0.5*(x*x+y*y-4.0)+4.0-px*px-py*py));
更に滑らかになりました。
「極端な例」の方はこうなります。

先程のものと同様にfを書き換えるとこうなります。

こちらは変化が小さいように見えます。
解説
この彩色法を発見した経緯を解説します。
マンデルブロ集合の外側の色の違いは、$${z_n}$$が発散したと判定されたときの$${n}$$の値の違いを表しています。

そして、同じ色のエリアの中では、発散判定がされたときの$${|z_n|^2}$$の値は外側の方へ行くほど大きく、内側に行くと小さくなります。
ということは、同じ色のエリアの境界線付近では以下のようなことが起こっていると予想できます。
内側の境界線付近では、$${|z_n|^2}$$の値は4より僅かに大きく、ギリギリで発散判定が起きている。
外側の境界線付近では、$${|z_{n-1}|^2}$$は4より僅かに小さいためギリギリ発散判定されず、$${|z_n|^2}$$が4から離れた値で発散判定されている。

ということは、$${f(0,y)=0}$$かつ$${f(x,0)=1}$$($${f(0,0)}$$は未定義でいい)という関数を作って、$${n+f(4-|z_{n-1}|^2,|z_n|^2-4)}$$を$${n}$$の代わりに使えば、彩色関数に代入する値を連続的に変化させられるのではないか、と考えました。
そして、$${f(x,y)=\frac{x}{x+y}}$$としたのがあのコードというわけです。
ところで、実はwikipediaの以下のページにも"Continuous coloring"という名前で似たような彩色方法が載っています。
しかし、こちらの方法では対数関数を組み合わせた複雑な関数を使っており、どうやら私が発見したものとは原理的に別物らしいです。
応用
応用です。

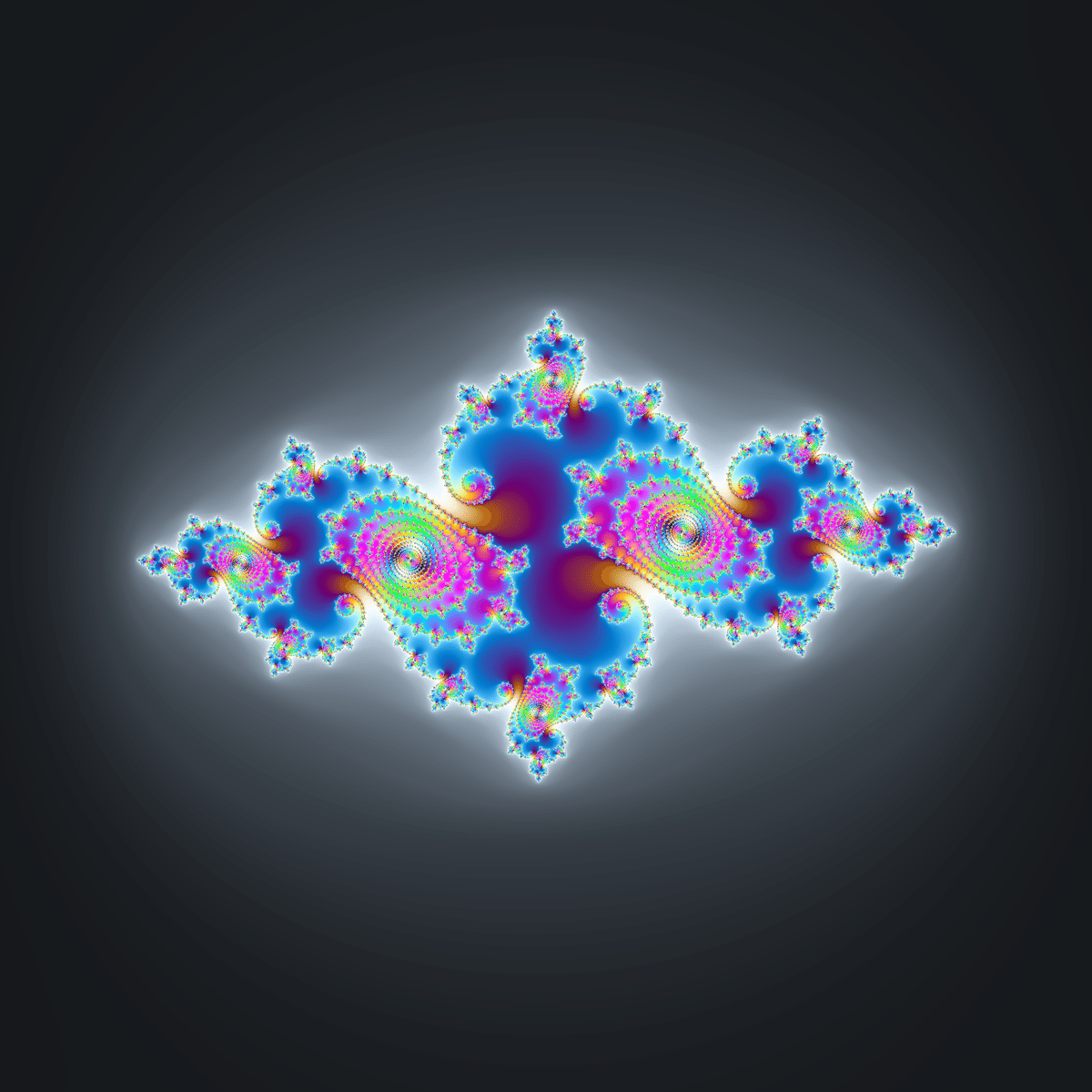

$${z^2+c}$$のジュリア集合でも、問題なく動作するようです。


別の種類のマンデルブロ集合でも動作するようです。

残念ながら2周期発散関数では上手く動作しません。

$${(0.9+0.5i)(z+\frac{1}{z})+c}$$のジュリア集合における色の境界は何やら特殊なようで、茶色と白の部分などのはっきりした境界線は消えていませんが、その他の薄い境界線は綺麗に消えています。
※☟(0.9+0.5i)(z+1/z)-0.7-1.4iのジュリア集合の通常の画像がある記事
