
今週のフラクタル11 ((0.9+0.5i)(z+1/z)+c)
どうも、108Hassiumです。
今週は$${(0.9+0.5i)(z+\frac{1}{z})+c}$$に関するフラクタル図形をお届けします。
(0.9+0.5i)(z+1/z)+c
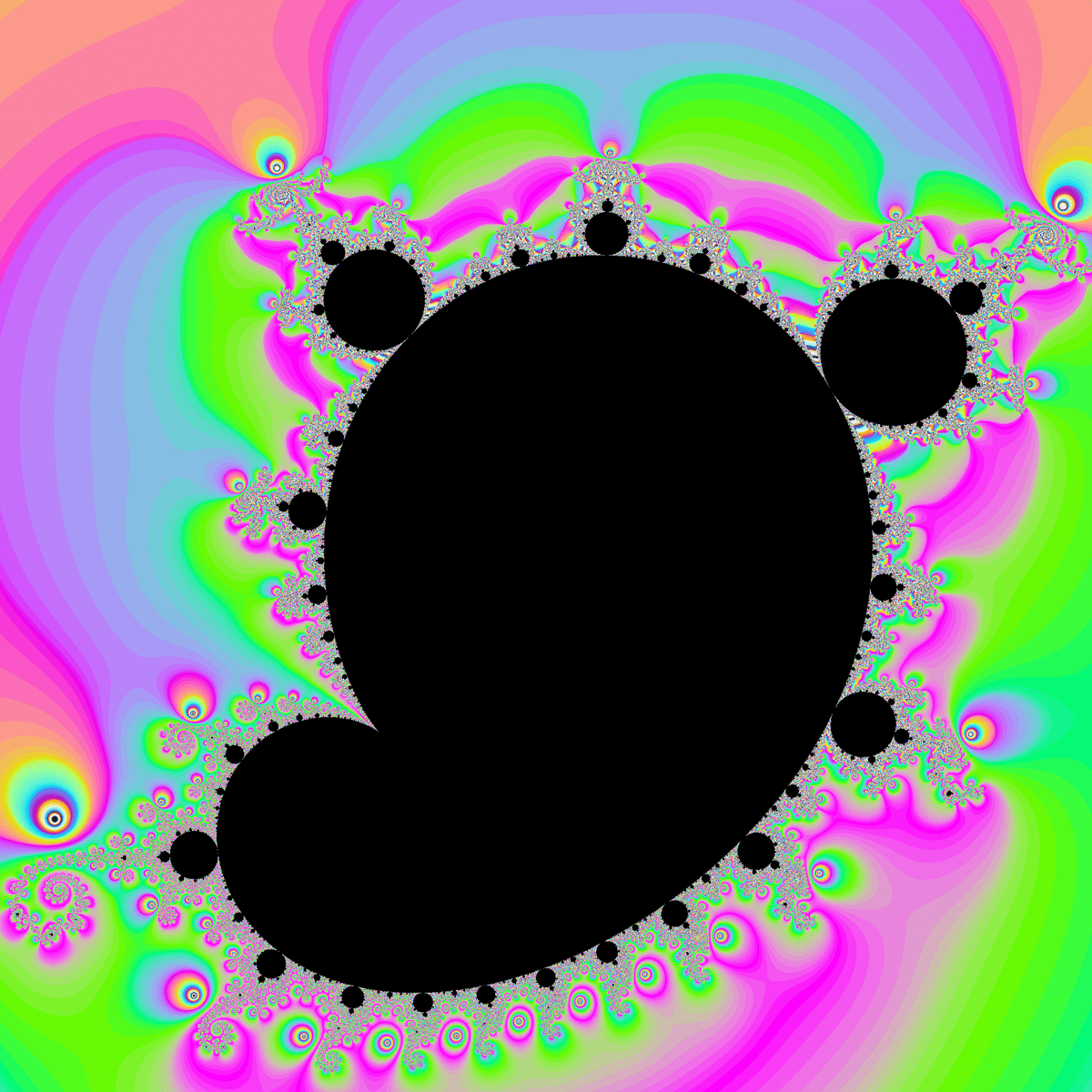
以下の記事で既に紹介した通り、$${|d|}$$が1よりちょっとだけ大きい場合、$${d(z+\frac{1}{z})+c}$$のマンデルブロ集合は外側がやたらカラフルになります。
ちなみに使用している彩色関数は、以下の記事で「雪解け」という名前で紹介しているものと同じです。(発散判定の閾値は変えてあります)



ジュリア集合もマンデルブロ集合と同様に、外側がカラフルになります。


$${z^2+c}$$のような普通(?)の関数では発散判定の閾値を上げても色が多少明るくなる程度ですが、この関数だと見た目が大幅に変化します。




この関数のジュリア集合の全体像は、やたらデカくなる傾向があります。





「今週のフラクタル」シリーズは、「暇な時にやっていた高周期ジュリア集合調査の記録」のストックを消費して書くときがあります。
上の5枚の画像も調査結果の画像なのですが、どうやら$${(0.9+0.5i)(z+\frac{1}{z})+c}$$の調査は新しい彩色関数の使用テストを兼ねていたらしく、収束領域の色合いが独特で他の記事の画像とはかなり雰囲気の異なるものになっていました。





いつものです。
コメントありがとうございます
note開設から約10か月、ようやく1件目のコメントをいただきました。

どうやらnoteのコメント欄には返信機能が無いようなので、ここに返事を書いておきます。
まず、コメントの文面をそのまま解釈すると「画像一枚ずつに必ず彩色法の説明をつけろ」と要求しているように読めますが、さすがにそんな無茶なことを言っているわけではないと思います。
このTobyさんは多分twitter上で交流のある@tobyhowardさんなのですが、この方はことあるごとにフラクタル画像の彩色・描画方法を訊いてきます。
今回もtwitterと同じノリで訊こうとしているんだと思いますが、noteでは記事の内容を絞り込んで主題と関係ない内容を極力削るようにしているので、彩色方法のような長い解説が要る話は気軽に触れることはできません。
今回の記事では$${(0.9+0.5i)(z+\frac{1}{z})+c}$$という関数の性質を語るためには彩色方法の話がどうしても必要であり、なおかつ既存記事の引用などで文章量を抑えることができ、さらにこのセクションで再度触れるという目的があったのでわざわざ彩色法の話を入れていましたが、基本的には主題と関係ない場面(特に今週のフラクタルシリーズ)では彩色方法の解説はしない方針とします。
彩色法に関しては、同系統のものをいくつかまとめたりそれを更に集約した記事をいつか投稿したいと思っているので、知りたい人はそれを待つかtwitterで個人的に訊いてください。(どちらも私の気分次第で解答が得られたり得られなかったりするので、期待せずに自分で研究してください)
