
せまゲー生半可集(11)~「Octal Game」……せまゲー界の『504』
前回の記事はこちら。
今回以降から、長丁場で数回続けていく予定です。
『504』とは
ボードゲームのデザイナーのなかで、一番の変態は誰か。
諸説ありますが、やはりFriedmann Friese(フリードマン・フリーゼ)さんです。
次々と発表するボードゲームは、なんというかクセがすごいのです。
その中でも、もっともクセがすごいボードゲームは何か、と問われれば
『504』
でしょう。
このボードゲームの凄さは、タイトルにあります。
このゲームで遊ぶことのできるゲームの数が504種類あるのです。
はっきりいってアホです。
なんでそんなことになってるのか。
ゲームのテーマが9種類あります。テーマを3つ選んで、それぞれ第一テーマ、第二テーマ、第三テーマと割り振ります。
この割り振りは、9×8×7=504、なのです。
【余談】
ちなみに、Friedmann Frieseさんは、自分の名前のイニシャル「FF」にあわせて、考案したゲームの大半は「頭文字Fの2単語」のタイトルにしています。
504は英語で「Five Hundred Four」なので、Five-Hundredとハイフンを入れると、「頭文字Fの2単語」になります。
しかし、ドイツ語だと「fünfhundertvier」なのですけどね。
細かいことは気にしないようにしましょう。
それぞれのテーマ即したベースとなるルールがあります。
これらを3つのルールを組み合わせるのですが、ルールの組み合わせによっては噛み合わなかったり矛盾が起きたりするので、例外処理のルール調整を加えつつ、なんとか整合性を保ちつつ、504種類のゲームを遊ぶようにしているようです。
よくぞまあ、作ったもんだ。
『504』ように、ルールを組み合わせてゲームをうみだすモジュール構造をもった、不偏ゲームがあります。
しかも、1960年代に。
それこそが、
Octal Game(オクタル・ゲーム(8進ゲーム))
です。
『Octal Game』とは
英語版のWikipediaに「Octal Game」の項があります。
これを日本語でまとめ上げたブログも見つけました。
『Octal Game(8進ゲーム)』は組合せゲーム理論の有名な書籍『数学ゲーム必勝法(Winning Ways for Your Mathematical Plays)』でも取り上げられています。
1960年代からある、としたのは、数学者の一松信さんが1968年に出版した『石取りゲームの数理』で「8進ゲーム」を取り上げているからです。
さて。
「8進ゲーム」とは、どのようなゲームか。
ざっというと、不偏ゲームの代表的基本ゲーム、「ニム(石取りゲーム、三山くずしなど)」をもとにして、ルールを拡張してみたもの、です。
ニムは、石の集まり(山)の1つから1つ以上石を取るアクションをします。
「8進ゲーム」では、「石を取ったあとの山の状態」に注目して、3つのルールを定義します。
(1)消滅:1つの山から石をすべて取り去って山がなくなる。
(2)残存:1つの山から石を取って、石1個以上の山が残る。
(4)分裂:1つの山から石を取って、石1個以上の2つの山に分ける。
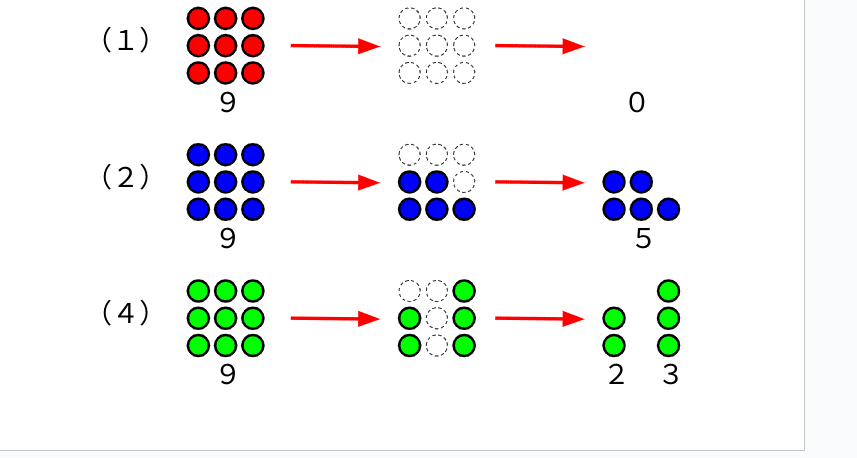
※なんで(3)がないのか、はちょっとしたポイントなので後述します。
いいかえると、石を取ったあとに山の数は、
(1)1つ減る(-1)
(2)増減しない(±0)
(4)1つ増える(+1)
ことになります。
さらに、「8進ゲーム」では、石を取る個数ごとに、この3つのルールの適用不可をきめます。
その表記は、小数の形式であらわし、小数の桁数が石を取る数と対応しています。
例えば、0.14307という表記は、
小数第一位:1
石を1個取るアクションは、消滅(1)しかできない。
小数第二位:4
石を2個取るアクションは、分裂(4)しかできない。
小数第三位:3
石を3個取るアクションは、消滅と残存(1+2=3)ができる。
小数第四位:0
石を4個取るアクションは、できない(0)。
小数第五位:7
石を5個取るアクションは、消滅・残存・分裂(1+2+4=7)ができる。
であらわされます。
なぜ、(3)がなかったかというと、消滅・残存・分裂の3つのルールの組合せを8進数であらわすためだったのです。
Octal Game 0.504
では、『OctalGame(8進ゲーム)』を試しに遊んでみます。
今回『504』をダシに使いましたので、ここでも働いてもらい、「0.504」でプレイします。
『8進ゲーム』のルールは、石の取り方を定めており、山の構成はまったくのノータッチです。
今回は『504』にあやかりまして、石5個の山と石4個の山の2つを用意して、すべての石を取って2つの山をなくしたプレイヤーが勝ちとします。

さて、石取りルール「0.504」はどういうことか。
小数第一位:5
石を1個取るアクションは、消滅と分裂(1+4=5)ができる。
小数第二位:0
石を2個取るアクションは、できない(0)。
小数第三位:4
石を3個取るアクションは、分裂(4)しかできない。
ちなみに、石を4個以上取るアクションはできません(これは、0.50400000000……とみなしルールを理解しております)
まず、石4個の山でできる石の取り方ですが「石を1個取り、石1個の山と石2個の山に分ける(分裂(4))」の1通りしかありません(下図の上矢印ルート)。
※「石を1個取り、石3個の山を残す」のは「残存(2)」のルールなので、できません(下図の中央矢印ルート)。
ちなみに、石を3個取るアクションは、石1個の山しか残らない「残存(2)」のルールにあたります。
※石3個取りのルールは、分裂(4)だけなので、できません(下図の下矢印ルート)。

残った石1個の山と石2個の山ですが、
・石1個の山は、石1個を取ることができます(消滅(1)ができるので)。
・石2個の山は、石1個を取るのは「残存(2)」ができないし、さらに、
石2個を取ること自体が不可(0)なので、実は石2個の山はこれ以上石を取ることができません。

2つの山をあわせて1手で終了となります。
つまり、石4個の山は、手番2手(つまり偶数)で終了となります。
次に石5個の山です。
3通りの石の取り方ができます。
(1)石を3個取り、石1個の山と石1個の山に分ける(分裂(4))
(2)石を1個取り、石2個の山と石2個の山に分ける(分裂(4))
(3)石を1個取り、石1個の山と石3個の山に分ける(分裂(4))

それぞれのその先の手番ですが、
(1)は、石1個の山から石1個を取る(消滅(1))アクションが2回できます。
(2)は、石2個の山から石を取ることができないので、ゲーム終了です。

(3)は、
・石1個の山をすべて取り(消滅(1))、石3個の山1つにする(下図の上矢印ルート)
・石3個の山から石1個を取り(分裂(4))、石1個の山3つにする(下図の下矢印ルート)
の2通りのアクションがあります。

どちらのアクションも、次のアクションは石1個の山2つになります。
結局、4回の手数ですべての石を取ることができます。
ということで、山5個での石取りアクションの回数は、
(1)3回
(2)1回
(3)5回
で、奇数回数です。
結果、全体(石5個の山と石4個の山)で石取りアクションの回数は、
奇数(石5個の山)+偶数(石4個の山)=奇数
なので、
実は先手が勝利するゲームとなっていました。
締め
ということで、『Octal Game(8進ゲーム)』の紹介でした。
ところで、ニムを『8進ゲーム』であらわす(1つの山から任意の数の石を取ることができて、山を分裂させない)と、
0.333333333333333333333333……
と無限に3(消滅と残存)が続きます。
次回は、『8進ゲーム』で表現ができる別のゲームを紹介します。
では。
