見出し画像

さらに、アインシュタインタイルでボードゲームの盤面をつくる。とにかく遊んでみる。

珍ぬ

前回の記事はこちら。

またもや引き継がず、話題はアインシュタインタイルに戻ります。

以前の記事、

では、論文「An aperiodic monotile」にあるHATの配置パターン（Substitution）をもとに、ボードゲームの盤面としてあつかってみました。

今回は、別論文の配置パターンで遊んでみます。

新しい論文

もうほんと、アインシュタインタイルの話題では何度もお世話になっている、日本テセレーションデザイン協会の代表である荒木義明さん。

秋山茂樹さんとの共同研究で、「HAT」の非周期的敷き詰めの別証明の論文「An alternative proof for an aperiodic monotile」を公開しました。

この論文にかかれている配置パターンは、その名も「Golden Hex Substitution（黄金六角形配置パターン）」です。


引用：An alternative proof for an aperiodic monotile p.２
Figure 1
https://arxiv.org/abs/2307.12322

４種類の配置パターン（上から、三角形のT、平行四辺形のPD、台形のZD、もう１つの台形のZT）からなります。

で、今回は代表してPDの３番めの図形（PD₃）を取り上げます。

【追記と訂正：2023/08/15】
荒木義明さんから「ここ書き間違いですよ」との指摘がありました。
最初の公開時点で、４種類の２番目を「TD」と表記しましたが、「PD」が正しいです。
その他、いくつか書き間違いがありましたので訂正しました。
大変失礼いたしました。


PD₃をつくってみる

論文ではTile($${\sqrt{3},1}$$)でかかれていますが、今回使用するタイルは「SPECTRES」でおなじみのTile(1,1)にします（後々の記事の構想もありまして……）。

毎度おなじみ、Tile(1,1)です。

とはいえ、PD₃ってどんな図形なのか、どんな盤面になるのかは、実際に作って確認してないと話になりません。

なので、必然的にPD₃をつくるための部分となる図形も用意しないとなりません。
結局、４種類の配置パターンの１番目――T₁、PD₁、ZD₁、ZT₁――をつくる羽目になります（ただし、T₁はタイル０個の図形なので、無視します）。

左：PD₁、中：ZD₁、右：ZT₁

ZD₁では１個、ZT₁では２個のTile(1,1)が、辺が赤色になっています。
これは他のタイルと異なり裏返しになっています。

さらに情報を付け加えると、PD₁はZD₁に含まれ（下図の黄色）、ZD₁はZT₁に含まれます（下図の水色）。

左：PD₁、中：ZD₁、右：ZT₁

さらにさらに。
論文「An aperiodic monotile」にあるHATの配置パターンH7、H8に含まれる、裏返しタイルの周辺を取り囲むタイル３個の配置も、ZD₁に１組（緑色）、ZT₁に２組あります（緑色と橙色）。

左：PD₁、中：ZD₁、右：ZT₁

これら３種を用いて、PD₃を作るこれまた途中段階として、PD₂とZT₂を作ります。

左：ZD₂、右：ZT₂

PD₂は、PD₁３個（橙色）、TD₁２個（水色）を組み合わせます。
ZT₂は、PD₁４個（橙色）、TD₁３個（水色）、ZT₁１個（緑色）を組み合わせます。

お待たせしました。

PD₂３個（黄色）、ZT₂２個（青色）を組み合わせて、これでようやっとPD₃が完成です。


盤面PD₃を愛でてみる

では、Tile(1,1)をマスとして盤面TD₃をみてみます。

盤面はおおよそ平行四辺形となっています。
短辺は９マス、長辺は１６マスとワイド画面的比率です。

なんとなくこのボードゲームで遊ぼうと連想してしまうのは『Hex（ヘックス）』です。

しかし、『ヘックス』は菱形でないと先手後手の有利不利の偏りがあります（長辺同士をつなげるには最低９マス、短辺側をつなげるには最低１１マス）。
短辺側の両端のマス（黒色の部分）を排除すれば、偏りが大分緩和されると考えます。

『ヘックス』以外のゲームだと、例えば以前の記事で紹介したMark Tompson（マーク・トンプソン）さんが考案した『Jade（ジェイド）』も遊べるかと思います。


さらに盤面PD₃を愛でてみる

もうすこし盤面PD₃をみてみます。
以前の記事でも、それぞれのマスは、（辺で）接しているマスがどれくらいあるのか確認しました。

盤面PD₃も確認してみます。
それぞれのマスが接しているマスの個数に合わせて色をつけてみます。
結果、このようになりました（ミスがあったらごめんなさい）。



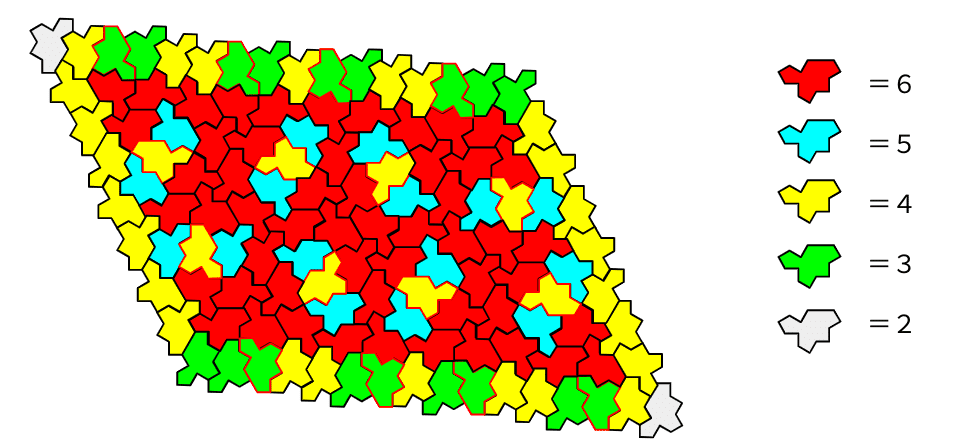
盤面の内側をみると、４マスしか接していないマスはすべて裏返しになっているマスになります。
５マスしか接していないマスも、裏返しマスを挟むかたちで現れています。

盤面の外側ですが、裏返しのマスは３マスしか接していません。
加えて、裏返しのマスの同方向の隣接マスも３マスしか接していません。

概ねのマスでは、正六角形マスのように振る舞っています。
裏返しマスのイレギュラーがいいアクセントとして働くかもしれません。


締め

ということで、またもやアインシュタインタイルに戻って盤面をつくって愛でてみました。

三角形のTや台形のZT、ZDもまだまだいじっておりません。
次回はこれらをいじるかもしれません。

では。

いいなと思ったら応援しよう！