
『山』を手書きでフラクタル表現してみる
『山』

フラクタル『山』

フラクタルフラクタル『山』

フラクタルフラクタルフラクタル『山』

フラクタルフラクタルフラクタルフラクタル『山』

やってみたかった
前回の記事はこちら。
しばらく、デュシャンに関わっていたので違った話題で気分転換しようと思いまして。
しかし、本来は別の話題があったのですが、ふと「山」をあんなふうに描くとどうなるか、見てみたくなりましてやってしまいました。
普通の山のフラクタル表現――何じゃ普通って?――は、例えば以下のサイトなど参考になるところはたくさんあります。

シェルピンスキーのギャスケット
今回描いた『山』ですが、お手本となったのは「シェルピンスキーのギャスケット(または、三角形、または、ざる)」です。

△のなかに「山」を描いて、下の横線は隣の「山」にもつなげてみたわけです。

あえて名付けるならば「シェルピンスキーの山」です。
シェルピンスキーとは、ポーランドの数学者Wacław Franciszek Sierpiński(ヴァツワフ・フランチェシェク・シェルピニスキ)さんのことです。
山とギャスケットとの差
さて、今回描いた『山』ですが「シェルピンスキーのギャスケット(三角形)」とどの程度の差があるのか、ちょいと気になります。
比較するのに、格子点を用いてみます。

三角形は(格子点も確認できる)内部がある表現として上から見た三角錐にしています。
山が占有する格子点は7個で、三角形は9個です。
2個の差は、三角形の底辺の2角の格子点です。
段階をすすめてみます。

まずは右の三角形。
1角で2つの三角形が隣接していることを考慮すると、全体の格子点の数はは9×3-3=24個となります。
左の山は、
・中央の縦線が新たに通る格子点1個を加える。
・底辺の両端の格子点2個を取り除く。
ので、都合1個増えて25個となります。
さらに、段階をすすめます。
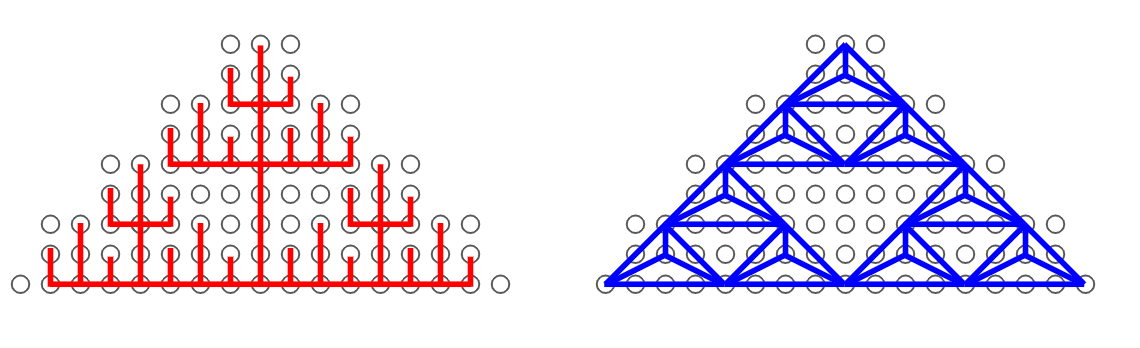
右の三角形は、前の段階にならってシンプルに求めることができます。
格子点は、
・前の段階の三角計の格子点の数:24個
・前の段階の三角計が重なり合う格子点の数:3個
24×3-3=69個。
左の山は、右の三角形にならって、
・前の段階の山の格子点の数:25個
・中央の縦線が新たに通る格子点:3個
から、25×3+3=78個です。
もういっちょいきますか。

同様に求めると、
右の三角形は、69×3-3=204個。
左の山は、78×3+7=241個。
なんとなしに、山の中央縦線の追加の格子点を加えていますが、
2の累乗引く1個で増えていきます。
数列で表すと、
三角形 $${ST_n}$$:$${ST_1=9,ST_n=3ST_{n-1}-3}$$
山 $${SM_n}$$:$${SM_1=8,SM_n=3SM_{n-1}+2^n-1}$$
です。
ちなみに、「シェルピンスキーのギャスケット(三角形)」の内部全体の格子点の数の数列は、
内部 $${T_n}$$:$${T_n=(2^n+1)^2}$$
つまり、9(=$${(2+1)^2}$$)、25(=$${(4+1)^2}$$)、81(=$${(8+1)^2}$$)、289(=$${(16+1)^2}$$)、……となります。
締め
ということで、ふと思いついたネタをやってみました。
意外とヘビーでした。
次回は飛ばしてしまった話題をやれればいいな、と思いますがどうなんでしょ。
では。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
