一橋大学2019数学（数列と確率だけ）（過去問解説）

お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。

今日は過去問解説にチャレンジします。

文系で最も難しいと言われる、一橋大学の数学を解説します。問題は載せませんのでご自分で参照してください。

なるべく「与えられた問題文をどう読むか」と言う点を重点的に解説していきたいと思います。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思います。模範答案も載せてません。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。あと、手間がかかる図形問題はお昼に時間が取れる日じゃないとやりません。

なので、今回は大問１と５の、言葉による説明が可能なものだけに絞って解説を作りました。

あと、数学って数式ばっかり使いやがってわかりづらいんだよ、みたいなのはうんざりで、計算に必要なルールを覚えてしまえば、言葉で説明できることばかりです。それにチャレンジしたいという気持ちがあります。ちなみにこれは自称中級者の人でも勘違いしがちなところだったりします。入試範囲では、数学で説明できないならそれは数学じゃないよ、と。

大問１（数列と論証）

平方数の定義は、自然数の２乗となる数。具体的には、1,4,9,16,25...

これぐらいは一橋大学の受験者ならわかっているはずで、問題で注目すべきは「数列{a_n}に平方数でない項が存在することを示せ。」です。

何かが存在することを示せ、と言われた時に考えるのは

①存在しないと仮定して矛盾を導く→背理法
②何か１つでも存在を示す

この２つです。どちらでも解けますので、両方解説します。

背理法の場合

全ての項が平方数だと仮定すると、当然ながら３番目の項も平方数である、それをq^2（qは自然数）とでも置いて、漸化式に適応してみると、qとpの二乗の差が12と言う方程式になります。

(q-p)(q+p) = 12

pもqも自然数の設定ですから、q-p < q+p でこの２式は共に自然数です。

よって(q-p,q+p) = (1, 12),(2,6),(3,4)のいずれかで、pとqが共に自然数となるのは(2,6)のときで、そのとき p = 2, q = 4。

続けて項を確認していくと、a_4 = 4^2 - 2^2 + 13 = 25、a_5=25-16+13=22となって、平方数でないものが現れます。ここで矛盾が生じるので、「平方数でない項が存在する」ことが示せました。

存在を示す場合

「全てが平方数である」と仮定をしないと、pを具体的に求めることはできないので、とりあえずそのままpを使って、項を求めていきます。

a_3 = p^2 - 12
a_4 = 25
a_5 = 26 - p^2
a_6 = 14 - p^2
a_7 = 1
a_8 = p^2

そうするとこれでループしてるのが判明します。整数関係ってループすることが多いですよね。余りとか。

６つずつでループしていると言うことは、その中に平方数でない数があるかどうか確かめられたら、存在を証明出来るわけです。

候補は

a_3 = p^2 - 12
a_5 = 26 - p^2
a_6 = 14 - p^2

の３つです。

ここで、式をよくみてみると、pの値によって正負の値が簡単に変わってしまいそうですね。定義上、負の整数は平方数にはならないので、絞り込めます。

平方数は正であるため、a_3が正であるにはpは4以上でなければなりません。しかし、そうするとa_6が確定で負になるので、pの値にかかわらず、どちらかは必ず平方数にはなれません。

このような感じで、存在を示していけば良いでしょう。他にも示す方法はありますので試してみてください。

大問５（確率）

まずは全事象の場合の数を考えます。

9マスからランダムで3マス選ぶので 9C3 = 84通り

（１）S=3のとき

これってつまり１列並ぶパターンを数えたら良いですね。斜めについては考慮しないと書いてあります（縦と横の各列について、と書いてある）ので

縦に１列：３通り
横に１列：３通り

の合計６通りです。書き上げても良いでしょう。

6/84 = 1/14

（２）S=1のとき

ルールに従うと、ちょうど２枚並ぶ列が１つだけしか存在しないとき、が求めるパターンです。とりあえずどこか一箇所、適当な列で試してみます（パターンが見つけにくいとき、試行するのは大切）。

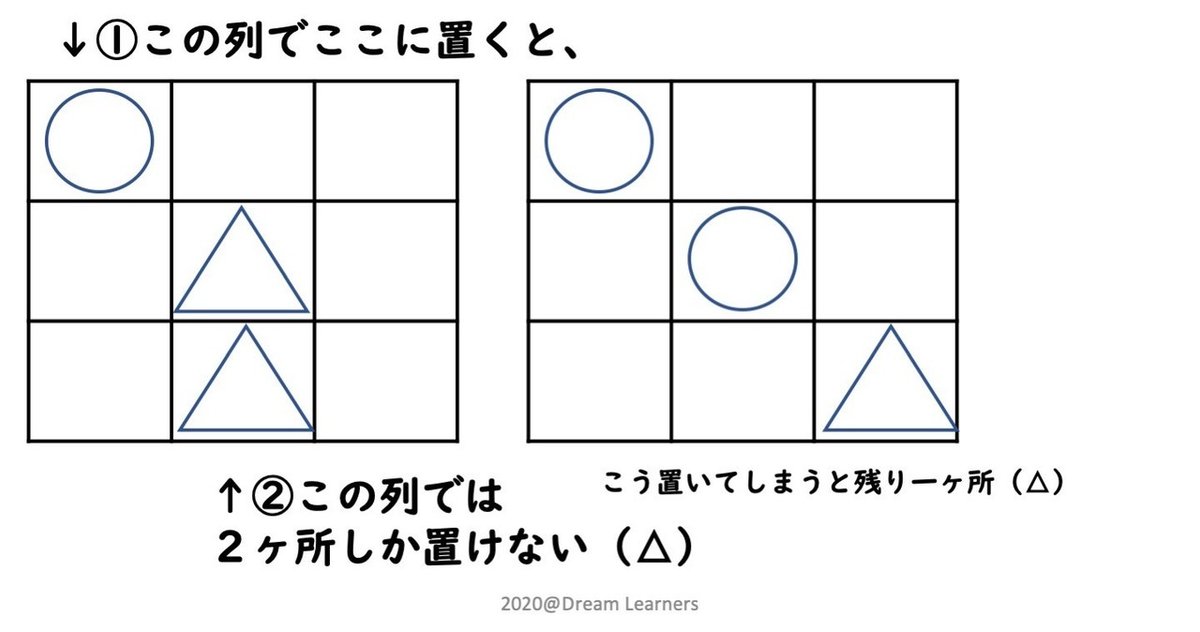
例えば、上図のように一番上の横の列に2個丸がつく場合には、空いている縦の列の２箇所が残り1個の丸を付けられる候補です。

ある列について、そこに２つ並べる場合の数は、どの１つに並べないか、と言う場合の数なので３通り。それぞれの場合について、空いた１つの別の方向の列（縦ならば横、横ならば縦）のうち、２ヶ所に置けるので２通り。

よって、１つの列について６通り、S=1となるパターンがあります。この列１つについての議論は、縦であっても横であっても対称性から明らかに、どの列が来ても同じ結論になります。不安ならさらに何個か試してみてください。

よって、S = 1となる場合の数は、列が６つあり、その列１つに月６通りあるので、３６通りあります。

36/84 = 3/7

（３）S=2のとき

まあ、ここまで誘導されていれば、やることは２つのうちどちらかでしょう。Sの値は、0,1,2,3のいずれかしか取りそうにありませんので、

①S = 2 の場合をストレートに数える
②S = 0 の場合を考えて、(1)(2)以外に残っている場合の数から引く

①はうまく数え上げるのがめんどくさそうなので、やめましょう。

②について、S = 0になる場合は、

３つの丸が、「どの縦・横の列にも２つ以上並ばない」

なので、左端から、縦横で重ならないように数えようとすると、

このように考えていけば、3箇所*2箇所*1箇所=6通りだとわかる。これぐらいなら別に書き上げても良いでしょう。

S = 0 ：6通り
S = 1 ： 36通り
S = 3 ： 6通り
全体：84通り

と数えておいたので、S = 2となる場合の数は、

 84 - ( 6 + 36 + 6 ) = 36通り

となって、求める確率は、(2)と同じ

36/84 = 3/7

補足：（３）でまともに数える場合

あまり、やる人はいないとは思いますが、そこまで難しくないので解説します。

これはS=2、すなわち、２つの列に２つずつ丸がついていると言うことですから、「列を２つ選んで、そこに２つずつ並ぶように配置できれば良い」と考えると早いです。

まず、これをやろうとすると、同じ方向の列は選べないのがわかります（4個必要）。なので、縦と横の列を１つずつ選び、そこに２つずつ並ぶよう（1個重なる）ように配置することを考えます。

で、１組選ぶごとに、並べ方は４通りです。どのように列を選んでもこの場合の数は変わりません。では、列を選ぶ場合の数は、縦３通り、横３通りですから、組み合わせは９通りです。

よって、S = 2となる丸の配置の場合の数は、4*9=36通りとなり、S = 0の場合を求めてから引いた場合と同様になります。説明は明らかにS = 0を考える方が楽だし早いので、本番でそちらに目が行けば他の面倒な問題を考える時間が増えたかな、と思います。

以上です

難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中！
LINEやSkypeによる無料相談も受付中！

【初回相談無料】ドリームラーナーズ