京都大学2020 理系数学 大問４ 整数

お世話になります。ドリームラーナーズの石原です。鳥取県倉吉市で進路指導と学習法指導の塾を運営しています。学習指導は中学生・高校生・大人、英語の指導は小学生から対応しています。LINEなどを活用して、遠隔地でも進路指導・学習指導に対応しています。

今日は過去問解説にチャレンジします。京都大学の理系数学の大問４です。問題本体は載せませんので、ご自分で用意してください。

なるべく「与えられた問題文をどう読むか、読んで何を考えるか」と言う点を重点的に解説していきたいと思います。あと、「いかに簡単に、楽して解くか」も重視します。数式を試行錯誤してぐちゃぐちゃやって解けた、と言う話はあまり参考にならないと思いますし、時間内に解ききれません。載せているのは考え方だけです。私が普段やっている指導では、これを小出しにしながら誘導していくスタイルを取っています。

大問４：問題を観察する

一見、何していいかわからないです。ただ、３で何回割れるか、と言うことを問われているので、少なくとも3の倍数である必要があります。なので、関数fの値自体が３の倍数になる時のm,nの条件を考えてみましょう。

幸い、nが3の倍数ではない、と条件が付けられていますから、以下の６通りを考えるだけで済みそうです。（以下全て、3を法とします）

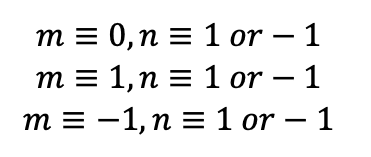
証明は端折りますが、この中で、そもそもf(m,n)が３の倍数になるのは以下の２パターンだけです。

こんな感じで、３で括って、その中身でさらに３の倍数の条件を作っていき、何回３が出せるか、と考えていきます。

…というところで、これは「合同式」を使えるようになっていないと物凄い時間がかかります。現行課程では教科書レベルの話ですから、できる人がほとんどだと思いますが、念のため。

大問４：何回３の倍数が作れるか…？

まず、すぐ終わってしまう方から検証します。これはとりあえずm,nを具体的な式にするところから始めます。k,lは整数とします

m,nの制限がきつい（０から３０までの整数）ので、本番ではk,lの範囲を書いておく方が良いです。

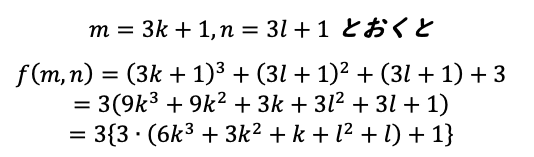
で、これはこれ以上、３の倍数を作れません。

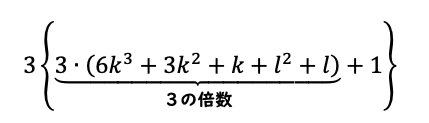
これだと、３で割れる回数は１回のみです。

では別の方を。

で、３でくくれたこの中身（＊）も、変数が余っているので、さらに３で割れる条件を探せそうです。

では進めます。

まだ行けそうです。

で、ここらへんで、そろそろnの候補が絞れそう（「３で割ったらいくつ余るか」を「３回」噛ませているので、２７が関わる整数になっている→候補が３０までなので余裕で絞れそう）なので、調べてみると、やっぱり、

こうなります。実際には、最初のk,lの時点で絞り込みを行っていれば気づくと思います。

この時、q=0で、p=1ですね、そうすると、

となり、

ここから先は具体的に入れてみれば良いでしょう。最終段階の式を活用すれば、検証は簡単です。

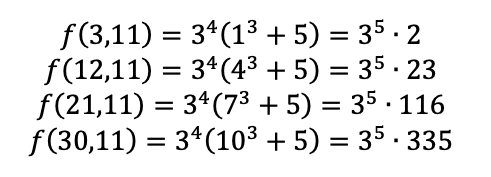
いずれの値も、５回以上は３で割れないので、求める最大値は５です。

本日は以上ですが、少し感想を…

今年の京都大学の問題の印象は、「難産」です。名古屋大のやばい時ほどではないですが、どういう着地点なのか見辛いのと、進めていく中で光明が見えづらいのと、単純に論証の難易度が高いです。この問題は、その中でも基礎に忠実に（３で割っていけるかどうか検証する）やればできる問題なので、解けておきたいところです。

難関大志望者の中で勝ち残る学習法を公式ウェブサイトで公開中！
LINEやSkypeによる無料相談も受付中！

【初回相談無料】ドリームラーナーズ