どっちが先？「四辺形」と「四角形」の謎(?_?)

　以前、名称の違いについて記事を書きました。↓↓

　このことを調べたときに、
　そもそも「四辺形」とは何か？「四角形」とは何か？
ということに、とても疑問をもちました。
　そして、どちらが先にできて、それに付随してどちらが出来上がるのか、とても興味をもったので、調べてみました！！

　最後まで読んでいただけると、うれしいです！！

１　結論

　「四辺形」が先で、それに付随して「四角形」ができる。

　これが結論です。

図１

　実は、色が塗ってあるかどうかが、結構ポイントです！！

　では、説明していきます。
　ちょっと難しいかもしれませんが、ついてきてください！！

２　折れ線

　まず、「折れ線」という言葉から定義します。

　平面上に$${n}$$個の相異なる点$${A_1, A_2, A_3.・・・.A_n}$$がある。
　このとき、$${n-1}$$個の線分$${A_1A_2, A_2,A_3, ・・・,A_{n-1}A_n}$$からなる図形$${L}$$を折れ線といいます。
　また、各$${A_i}$$を$${L}$$の頂点、各線分$${A_{i-1}A_i（$${i=2, 3, ・・・, n}$$）を$${L}$$の辺といいます。

　ややこしいので、図をかきます。
　下の図の折れ線の$${A_1, A_2, A_3, A_4, A_5}$$が頂点、線分$${A_1A_2, A_2A_3, A_3A_4, A_4A_5}$$が辺です。

図２　折れ線

・　単純折れ線

　折れ線のどの２辺についても、隣り合う辺$${A_{i-1}A_{i}}$$と$${A_{i}A_{i+1}}$$の共通の頂点$${A\i}$$以外には、共有点をもたないとき、特に単純折れ線といいます。

図３　単純折れ線

３　閉折れ線と多辺形と単純閉折れ線

　次に、$${n}$$個の線分$${A_1A_2, A_2,A_3, ・・・,A_{n-1}A_n, A_{n}A_1}$$からなる図形$${C}$$を閉折れ線といいます。

図４　閉折れ線

　$${n}$$個（$${n}$$は3以上）の線分からなる閉折れ線$${C}$$のどの2辺についても、それらの共有点が0個または1個のとき、$${C}$$を$${n}$$辺形といい、$${n}$$辺形を総称して多辺形といいます。

図５　閉折れ線と５辺形

　この上の５辺形、想像したのと違いませんか？

　実は、もう少し用語を定義する必要があります。

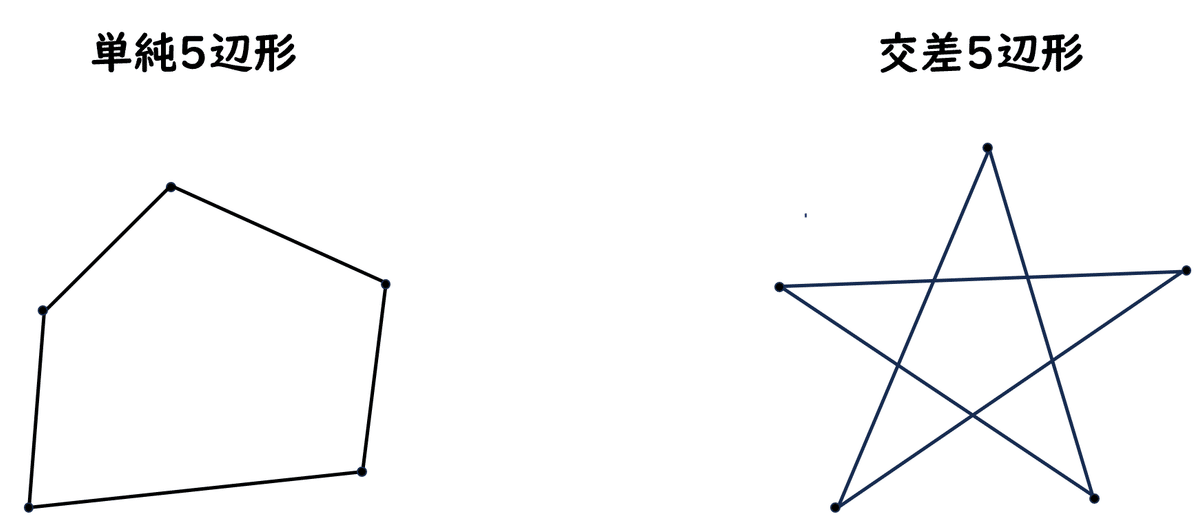
　$${n}$$辺形$${C}$$において、そのどの２辺についても、隣り合う２辺の共通の頂点以外には、共有点をもたないとき、$${C}$$を単純閉折れ線、または、単純$${n}$$辺形といい、単純$${n}$$辺形を総称して、単純多辺形といいます。
　単純でない多辺形を、交差多辺形といいます。

図６　単純５辺形と交差５辺形

４　多角形

　単純$${n}$$辺形$${C}$$と、その内部領域を合わせた図形を、$${C}$$を境界とする$${n}$$角形といいます。$${n}$$角形を総称して、多角形といいます。

図７　単純５辺形と５角形

　ということで、$${n}$$辺形を作るから、それに付随して$${n}$$角形ができる、となります。

　これで、疑問が解決となります。

５　おわりに

　何気なく感じた疑問でしたが、調べてみると面白かったです。

　ちなみにこの上で調べたことから、内部領域を含んでいるのは「多角形」です。
　じゃあ、
　平行四辺形の面積を求めなさい。
は、
　平行四角形の面積を求めなさい。
という問い方が正解なのでしょうか。

　読者の皆さんは、どちらか正しいと思いますか？？
　もしよければ、コメント欄で意見をいただけるとうれしいです！！

　最後まで読んでいただき、ありがとうございました！