
岡潔さんが中学5年生のときに考えていた問題を解いてみた!!
こんにちは。
最近数学者の岡潔さんの著作にどっぷり浸かっております。
それは、以前記事に書いたのですが、「人間の建設」という本を読んでから、とてもこの方の考えに感銘を受けたからです。
今回の記事は、岡潔さんが書かれた著作の中に、ちょっとだけ書かれていた問題で、私にも解けそうだなと思ったので記事にしてみました。
証明は載せますが、数学が苦手な方でも見て楽しいでもらえるように、図も多く載せていきますので、最後まで読んでいただけるとうれしいです。
1 問題
さて、まずは取り組む問題からです。
完全四辺形の三つの対角線の中点は同一線上にあることを証明せよ
完全四辺形とは、以下のような図形です。

証明することを、図にすると、以下の通りです。
図2の赤丸、青丸、黄色の丸は、それぞれ対角線の中点(真ん中の点)です。
その3つの点は、実は1本の直線上にあるから証明して!!です(笑)

岡さんは、この問題に、このように取り組んでいたようです。
家の南の出口のたたきのところで、消し炭を使って図を描いては考え込んでいた。これを冬休みに入っても続けていたところ、正月前にとうとう鼻血を出してしまい、まるで睡眠薬中毒みたいにこのあとずっと気持ちが悪くなって、冬休み中はなおらなかった。
う~ん。
私も鼻血が出るまでできるかわかりませんが、粘ってみます(笑)
また、このようなことがあってから、
かなりよく考えるようになった
とあるので、このように熱中する経験は必要かもしれませんね。
2 本当に一直線上にあるの?
そもそも本当に一直線上にあるのか。
実際に作図して調べてみました。
作図する四角形は、完全四角形にならないといけないので、辺を延長する前の四角形は、台形はだめです。
もちろん平行四辺形やひし形、長方形、正方形も。
次に辺を延長する前の四角形のパターンとして、次の4パターンを考えました。
ここで、鈍角とは90°より大きく180°より小さい角です。
鈍角が1つだけある四角形
鈍角が2つで、それが隣り合っている四角形
鈍角が2つで、向かい合っている四角形
鈍角が3つある四角形
まず鈍角が1つだけある四角形です。

3つの中点は1本の直線状にあります。
次に鈍角が2つで、それが隣り合っている四角形です。

3つの中点が1本の直線上にありそうです。
ちょっとずれているのは、おそらく私の雑さでしょう。
すみません(´;ω;`)ウゥゥ
次に鈍角が2つで、それが向かい合っている四角形です。
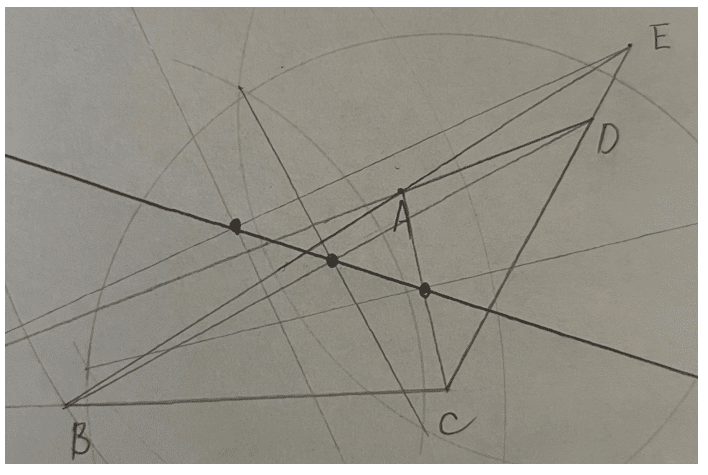
これは3つの中点がちゃんと1本の直線上にありますね。
最後に鈍角が3つある四角形です。

これも3つの中点がちゃんと1本の直線上にありますね。
ということで、どのパターンも1本の直線上にありそうです。
これを最初に思いついた人、すごいですね(;・∀・)
3 証明までの道のり
ここからはがっつり高校の数学を使っていきます。
もし苦手な方は、「5 おわりに」へ飛んでください。
数学アレルギーが発症してしまっては手遅れですΣ(゚Д゚;≡;゚д゚)
高校生の方であれば、良い練習問題になると思うので、取り組んでみてください!!
では、まず証明するために使えそうな知識です。
高校生なら、このように一「直線上にあることを証明」なら、ベクトルだと予想しますよね。
私もベクトルで証明します。
次に、証明するための適切な図をかきます。
図は数学にとって、とても大切ですね!

また、対角線OC , AB , DEの中点をそれぞれE , F , Gとします。
次に、$${s>1 , t>1}$$を用いて、$${\overrightarrow{OD}=s\overrightarrow{OA} , \overrightarrow{OE}=t\overrightarrow{OB}}$$とします。
さて、一直線上にあることを示すには、$${\overrightarrow{EF}=k\overrightarrow{FG}}$$を示せばOK。
ただし、$${k}$$は実数です。
つまり、$${\overrightarrow{OE} , \overrightarrow{OF} , \overrightarrow{OG}}$$を$${s,t,\overrightarrow{a} , \overrightarrow{b}}$$で表せればいいです。
それができなさそうなのは、$${\overrightarrow{OE}}$$です。
なぜなら、$${\overrightarrow{OC}}$$が$${s,t,\overrightarrow{a} , \overrightarrow{b}}$$を使って表せないからです。
ここで活躍するのが、メネラウスの定理です。
・ メネラウスの定理

メネラウスの定理の証明

BDと平行な直線AFをかきます。
△OBDで、BD//FAより、
$${\frac{OD}{DA}=\frac{OB}{BF}}$$ ・・・①
△EFAで、BC//FAより、
$${\frac{AC}{CE}=\frac{FB}{BE}}$$ ・・・②
よって、
$${\frac{OD}{DA}・\frac{AC}{CE}・\frac{EB}{BO}}$$
は、①、②より
$${\frac{OB}{BF}・\frac{FB}{BE}・\frac{EB}{BO}=1}$$
と言えます。
4 問題の証明
・ AEの内分点Cの内分比を求める
$${AC:CE=x:(1-x)}$$とします。

このとき、△EOAと直線BDでメネラウスの定理を使う。

$${\frac{OD}{DA}・\frac{AC}{CE}・\frac{EB}{BO}=1}$$
$${\frac{s}{s-1}・\frac{x}{1-x}・\frac{t-1}{1}=1}$$
$${\frac{x}{1-x}=\frac{s-1}{s(t-1)}}$$
これを$${x}$$について解く
$${(st-s)x=s-1-(s-1)x}$$
$${(st-1)x=s-1}$$
$${x=\frac{s-1}{st-1}}$$
・ ベクトルOE, OF, OGをベクトルa, bで表す
$${\overrightarrow{OA}=\overrightarrow{a} , \overrightarrow{OB}=\overrightarrow{b}}$$とします。
点EはOCの中点だから、
$${\overrightarrow{OE}=\frac{1}{2}\overrightarrow{OC}}$$
$${\overrightarrow{OC}=\overrightarrow{a}+\frac{s-1}{st-1}\overrightarrow{AE}}$$
ここで、$${\overrightarrow{AE}=t\overrightarrow{b}-\overrightarrow{a}}$$だから、
$${\overrightarrow{OC}=\overrightarrow{a}+\frac{s-1}{st-1}(t\overrightarrow{b}-\overrightarrow{a})}$$
$${=\frac{st-s}{st-1}\overrightarrow{a}+\frac{st-t}{st-1}\overrightarrow{b}}$$
$${\overrightarrow{OE}=\frac{st-s}{2(st-1)}\overrightarrow{a}+\frac{st-t}{2(st-1)}\overrightarrow{b}}$$

次に、点FはABの中点だから
$${\overrightarrow{OF}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}}$$

最後に、点GはDEの中点だから
$${\overrightarrow{OG}=\frac{1}{2}s\overrightarrow{a}+\frac{1}{2}t\overrightarrow{b}}$$
・ 点E, F, Gが一直線上にあることを示す
上述したことをもう一度かきます。
$${\overrightarrow{OE}=\frac{st-s}{2(st-1)}\overrightarrow{a}+\frac{st-t}{2(st-1)}\overrightarrow{b}}$$
$${\overrightarrow{OF}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}}$$
$${\overrightarrow{OG}=\frac{1}{2}s\overrightarrow{a}+\frac{1}{2}t\overrightarrow{b}}$$
$${\overrightarrow{EF}=\overrightarrow{OF}-\overrightarrow{OE}}$$
$${=\frac{st-1-st+s}{2(st-1)}\overrightarrow{a}+\frac{st-1-st+t}{2(st-1)}\overrightarrow{b}}$$
$${=\frac{s-1}{2(st-1)}\overrightarrow{a}+\frac{t-1}{2(st-1)}\overrightarrow{b}}$$
$${=\frac{1}{2(st-1)}((s-1)\overrightarrow{a}+(t-1)\overrightarrow{b})}$$

$${\overrightarrow{FG}=\overrightarrow{OG}-\overrightarrow{OF}}$$
$${=\frac{1}{2}s\overrightarrow{a}+\frac{1}{2}t\overrightarrow{b}-\frac{1}{2}\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}}$$
$${=\frac{s-1}{2}\overrightarrow{a}+\frac{t-1}{2}\overrightarrow{b}}$$

よって、
$${\overrightarrow{FG}=\frac{1}{st-1}\overrightarrow{EF}}$$
これで、点E, F, Gが一直線上にあるといえました。
5 おわりに
さて、今回は対角線の交点が一直線上にあることについて考えました。
実はこの直線、名前があります。
ニュートン線と呼びます。
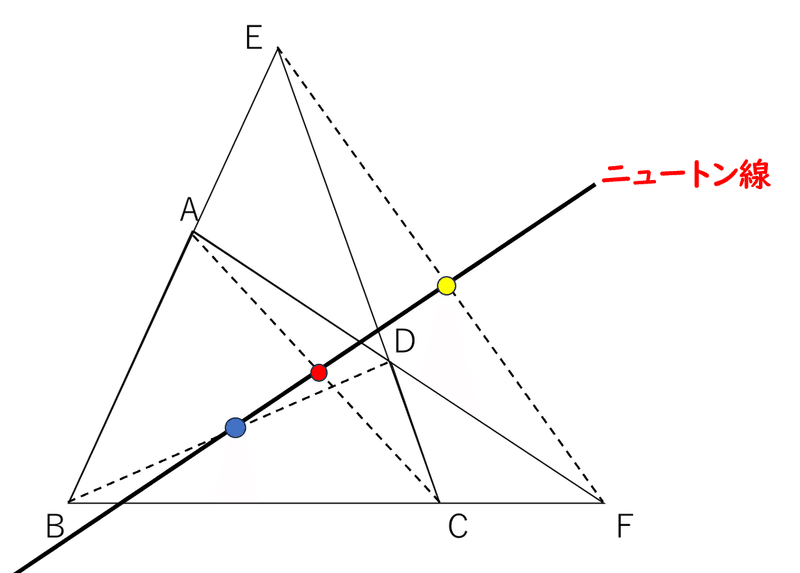
このニュートン線については、次のような性質もあります。
四角形ABCDの向かい合う辺の中点を結んだ直線の交点は、ニュートン線上にある。

作図してみると、たしかに言えそうですね。
もし興味がありましたら、取り組まれてみてください!!
予想ですが、アンの定理というのが使えるかもしれません。
また、プリュッカーは、次のことを証明しています。
完全四辺形の3本の対角線を直径とする3つの円は2点を共有し、その2点は4つの三角形の垂心を結んだ直線上にある。
今回はベクトルを使いましたが、解析的にできないかな~と試行錯誤したのですが、文字が多く出てきて挫折してしまいました。(´;ω;`)ウゥゥ
「春宵十話」に出てくる面白い定理をもう一つ他の記事で紹介します!!
最後まで読んでいただきありがとうございました!!

この記事が気に入ったらサポートをしてみませんか?
