【ラ・サール中学校2021年度入試算数第4問】割と素直な平面図形問題

第4問は平面図形の問題です。難関校ですが、それほど難しいという感じではありません。

ラ・サール中学校・高等学校
2010年7月22日、 Sakoppi撮影、Wikipediaより

問題

図の五角形 ABCDE において、四角形 ABCD は長方形、三角形 ADE は四角形 ABCD と面積が等しい正三角形です。次の問に答えなさい。(16点)

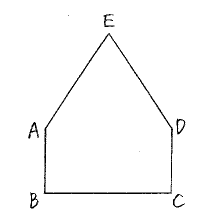
(1) 直線 EB でこの五角形はどのような面積比に分けられますか。

(2) 辺 DE のまん中の点を M とすると、直線 MB でこの五角形はどのような面積比に分けられますか。

(3) 次のア、イ、ウを正しくうめなさい。
「(2) の点 M と五角形の辺(　ア　)を(　イ　)：(　ウ　)にわける点を通る直線は、この五角形の面積を二等分します。」

解答解説

この問題でまず考えるべきは、正三角形ADEの高さと辺ABの関係です。
・正三角形 ADE = AD × 高さ ÷ 2
・四角形 ABCD = AD × AB
で、正三角形 ADE = 四角形 ABCD となることから、正三角形 ADE の高さ = 2 × AB となります。

これが分かれば、問題は解けたも同然です。

直線 BC、BC と平行で点 E を通る直線、直線 AB、直線 CD で囲まれた長方形を面積の基準とします。この長方形を FBCG とします。(下の図を見てもらうとわかりやすいです。)

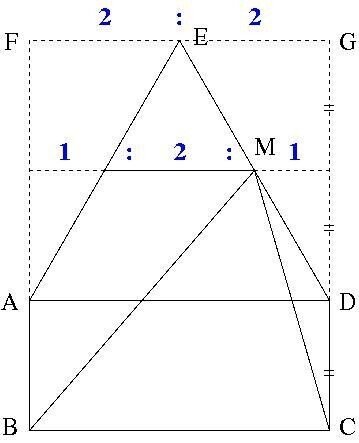
すると、長方形 ABCD は長方形 FBCG の 1/3 倍となるので、五角形 ABCDE はその2倍、長方形 FBCG の 2/3 倍となります。

(1) は三角形 ABE の面積を求めればいいので、AB = (1/3) × FB、EF = (1/2) × GF = (1/2) × AD から、三角形 ABE の面積は長方形 FBCG の面積の (1/3) × (1/2) × (1/2) = (1/12) 倍となります。

したがって、三角形 ABE の面積は五角形 ABCDE の (1/12) ÷ (2/3) = (1/8) 倍となるので、直線 EB は五角形 ABCED の面積を (1/8) : (1 - (1/8)) = 1 : 7 に分けます。

(2) も同じように考えますが、四角形 BCDM を三角形 BCM と三角形 CDM に分けて考えます。

三角形 BCM は辺 BC を底辺として考えると、M は DE のまん中の点であることから、BC = AD、高さ = (2/3) × FB となるので、三角形 BCM の面積は長方形 FBCG の面積の 1 × (2/3) × (1/2) = (1/3) 倍となります。

また、三角形 CDM は辺 CD を底辺として考えると、CD = (1/3) × FB、高さ = (1/2) × EG = (1/2) × (1/2) × AD = (1/4) × AD となるので、三角形 CDM の面積は長方形 FBCG の面積の (1/3) × (1/4) × (1/2) = (1/24) 倍となります。

以上のことから、四角形 BCDM の面積は長方形 FBCG の面積の (1/3) + (1/24) = (9/24) 倍となり、五角形 ABCDE の面積の (9/24) ÷ (2/3) = (9/16) 倍となります。

よって、直線 BM は五角形 ABCDE を (9/16) : (1 - (9/16)) = 9 : 7 に分けます。

(3) は (2) において三角形 BCM の面積が五角形 ABCDE の面積の半分であったことに注意するといいでしょう。

ですから、三角形 BHM = 三角形 CDM となるように点 H を辺 BC 上にとり、直線 MH で五角形 ABCDE で分けると、面積が二等分されることになります。

三角形 CDM の面積は長方形 FBCG の面積の (1/24)倍であり、底辺を BH としたときの三角形 BHM の高さは FB の (2/3) 倍なので、BH の長さは BC の長さの (1/24) × 2 ÷ (2/3) = (1/8) 倍であればいいことになります。

よって、H は辺 BC を (1/8) : (1 - (1/8)) = 1 : 7 に分けることになるので、ア = BC、イ = 1、ウ = 7 となります。

感想

この問題は、もちろんやさしくはないのですが、かといって難関中学校の入試問題としては難しくはないと思います。むしろ素直な部類です。

全ては正三角形の高さとABの長さの関係に気が付くかどうかだと思います。

(3) については、「三角形 BCM の面積が五角形 ABCDE の面積の半分」であることに気が付かなかったとしても、四角形 MHCD の面積が長方形 FBCG の 1/3倍になる、すなわち、三角形 MHC の面積が長方形 FBCG の (1/3) - (1/24) = 7/24倍になるように H をとることが分かれば問題ありません。

このとき、辺 HC を三角形 MHC の底辺として考えれば、HC は BC の (7/24) × 2 ÷ (2/3) = 7/8 倍であればよいとわかります。

あとは全体的にそつなく効率的に問題を解いていけるか、問題を解くスピードが問われると思います。

ちなみに、この問題では比をどの順番で書くかを指定していないので、(1) 7 : 1、(2) 7 : 9 としていいでしょう。

(3) に関しては、アの書き方でイとウが変わります。
・ア = BC の場合は イ = 1、ウ = 7
・ア = CB の場合は イ = 7、ウ = 1
です。それ以外は誤りです。(ア = BC で 2 : 14 とした場合は減点、ア = BC で 7 : 1 とした場合は × だと思います。)