【灘中学校2021年度入試(2日目)算数第4問】根性勝負？の数え上げ

今回は数え上げの問題ですが、残念ながら私にはきれいに解く方法は思いつきませんでした。しかし、ある意味で現実的な解き方だと思います。

灘中学校・高等学校
2011年8月28日、Saoyagi2撮影、Wikipediaより

問題

はじめ，3枚のカード①，②，③が左からこの順に並んでいます。こららのカードの並べ替(か)えを何回かします。1回の並べ替えにつき，次の (A) ～ (D) のどれか1つが行われます。

(A) 最も左にあるカードを右端(はし)に移動させる
(B) 最も右にあるカードを左端(はし)に移動させる
(C) 最も左にあるカードを残り2枚の間に移動させる
(D) 最も右にあるカードを残り2枚の間に移動させる

例えば，1回目に (A)，2回目に (C) の並べ替えをすると，カードの並びは
　　　　　①②③　→　②③①　→　③②①
と変化します。

(1) 下(原文は右)の図で，線でつながれた並びどうしは，(A) ～ (D) のいずれか1回の並べ替えで変わります。下の図の9つの空欄(らん)に 1 ～ 3 のいずれかの数字を入れなさい。

(訂正) 次の分を追加する。「下の図の6つの並びは，どの2つも異なります。」

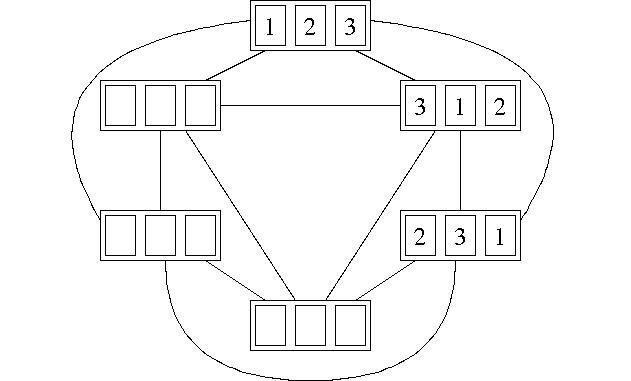
(2) 3回の並び替えで初めて①②③の並びに戻(もど)るような，3回の並び替えの方法は全部で(　　　)通りあります。

(3) 5回の並び替えで初めて①②③の並びに戻(もど)るような，5回の並び替えの方法は全部で(　　　)通りあります。

(4) (3) の並び替えのうち，(A) の並べ替えの回数と (B) の並べ替えの回数の合計が 5回であるものは全部で(　　　)通りあります。

(5) (3) の並び替えのうち，(A) の並べ替えの回数と (B) の並べ替えの回数の合計が 1回または 3回であるものは全部で(　　　)通りあります。

(注) 四角で囲った1, 2, 3 を出すことができないため、①, ②, ③ で代用しています。

解答解説

(1) はいきなり答えでいいでしょう。

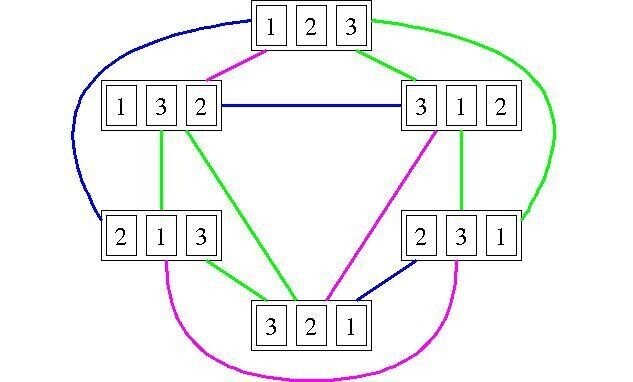
①②③ ⇔ ③②①、①③② ⇔ ②③①、②①③ ⇔ ③①② は互いに1回の並び替えでは到達できないことに注意してください。

また、上の図の線の色は、緑は (A) または (B) の並べ替え、青は (C) の並べ替え、ピンクは (D) の並べ替えを表しています。

(2) は、①②③からどの並べ替えを選択したとしても、行きついた並びからの並べ替えで1つは①②③、1つは③②① に着いてしまうので、残り2通りしか選択できない。そのそれぞれで①②③へ戻る並べ替えが1つあるので、全部で 4 × 2 × 1 = 8通りとなります。

(3) ですが、最初の3回の並べ替えと、残りの2回の並べ替えに分けて考えます。

まず、残りの2回の並べ替えを考えます。
・③②①からは4つのどの並べ替えを選んでも、次の並べ替えで①②③に戻ることができるので4通り
・①②③と③②①以外の並びからは、並び替えの1つは①②③へ、1つは③②①に着くので、残りの2つの並び替えしか使うことができず、それぞれ2通り

次に、最初の3回の並べ替えを考えます。条件を無視すると全部で4 × 4 ×4 = 64通りありますが、その中から条件に合わないものを捨てていきます。

また、最初に (A) を選ぶことと (B) を選ぶこと、(C) を選ぶことと (D) を選ぶことは左右の違いがあるだけなので、(A) と (C) の場合のみを考えればいいことが分かります。

ということで、32通りを考えればいいので、全列挙してもいいかと思います。

・AAA → ①②③へ戻るのでNG
・AAB → ②③①
・AAC → ①③②
・AAD → ③②①
・ABで①②③に戻るのでNG
・ACB → ②①③
・ACA → ①③②
・ACC → ②③①
・ACD → ③①②
・ADA → ①③②
・ADB → ③②①
・ADC → ①②③へ戻るのでNG
・ADD → ②③①
・CAA → ③②①
・CAB → ②①③
・CAC → ③①②
・CAD → ①②③に戻るのでNG
・CBA → ②①③
・CBB → ①③②
・CBC → ②③①
・CBD → ③①②
・CCで①②③に戻るのでNG
・CDA → ③①②
・CDB → ①②③に戻るのでNG
・CDC → ③②①
・CDD → ②①③

この中で ③②①に着く場合と、それ以外の場合に分けると、
・③②①が4通り
・それ以外が 16通り
あるので、(4 × 4 + 16 × 2) × 2 = 96通りとなります。

(4) と (5) ですが、問題であらかじめ与えられた並びをグループ1、それ以外をグループ2とおくと、(C) と (D) はグループ1とグループ2を結ぶので、①②③へ戻るとき、(C)もしくは(D)を使う回数は偶数となります。したがって、(4) の場合と (5) の場合は補事象となります。

(4) は AABAB と BBABA しか存在しないので2通り、(5) は 96 - 2 = 94通りとなります。

感想

以下に (3) の別解を書いておきます。①②③と③②①以外をその他と呼びます。

・①②③→その他は4通り(その他のそれぞれから①②③へは1通り)
・③②①→その他は4通り(その他のそれぞれから③②①へは1通り)
・その他→その他は2通り

であることに注意してください。(①②③⇔③②①は0通りです。)

①②③から③②①へ3回の並べ替えで到達する方法は、①②③→その他→その他→③②①以外にないので、4 × 2 × 1 = 8通りあります。

①②③からその他へ3回の並べ替えで到達する方法は、①②③→その他→その他→その他、もしくは、①②③→その他→③②①→その他、があり、
・①②③→その他→その他→その他は、4 × 2 × 2 = 16通り
・①②③→その他→③②①→その他は、4 × 1 × 4 = 16通り
あります。16 × 2 = 32通りあります。

あとは上で計算したように、③②①から①②③へ2回の並べ替えで到達する方法は4通り、その他から①②③へ2回の並べ替えで到達する方法は2通りなので、8 × 4 + 32 × 2 = 96通りと求まります。

この方法が (3) を解くのに一番効率が良いと思いますが、これを試験の中で見つけられるかは疑問です。難しいと思います。

最初に書いた方法は、初見で「32通りなら書くか」と判断して作成したものです。実際には(A) → (B) のように明らかに消える場合があって、確認するのは24通りだけということもあります。

この辺りは時間とのかねあいになると思います。

また、(4) はともかく、(5) は今回の中で最も難しいかもしれません。解答欄は答えだけなので、ヤマをはって 96 - 2 = 94通りと書いていいと思います。