【渋谷教育学園幕張中学校2021年度入試算数第5問】平面を駆使する立体問題

さて、今回で渋幕の問題は最後となります。(1), (2) はザコキャラですが、(3) はボスキャラにふさわしい難問です。はっきり言って、合否には全く関係ないと思います。

渋谷教育学園幕張中学校・高等学校
2008年6月20日、Kattin撮影、Wikipediaより

問題

図1 のように，底面がひし形で，側面がすべて長方形である四角柱 ABCD-EFGH があります。点 K, L, M, N はそれぞれ辺 AB, BC, CD, DA 上にあり，AK : KB = AN : ND = 1 : 1 で，BL : LC = DM : MC = 2 : 1 です。また，点 O はひし形 EFGH の対角線 EG 上にあり，EO : OG = 1 : 5 です。四角形 KLMN の各頂点と点 O をそれぞれ結び，四角すい O-KLMN をつくります。

このとき，次の各問いに答えなさい。

ただし，角すいの体積は，(底面積) × (高さ) ÷ 3 でもとめられるものとします。

(1) 四角すい O-KLMN の体積は，四角柱 ABCD-EFGH の体積の何倍ですか。

(2) 辺 AE, BF, DH のそれぞれの真ん中の点を通る平面で四角すい O-KLMN を切るとき，切り口の面積はひし形 ABCD の面積の何倍ですか。

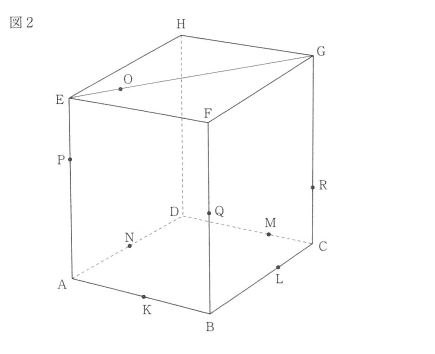
(3) 点 P, Q, R を，それぞれ辺 AE, BF, CG 上に AP : PE = 2 : 1，BQ : QF = 1 : 1，CR : RG = 1 : 2 となるようにとります。図2 は，図1 に点 P, Q, R をかき加えたものです。点 P, Q, R を通る平面で四角すい O-KLMN を切って 2つの立体に分けるとき，点 O を含むほうの立体の体積は，四角すい O-KLMN の体積の何倍ですか。

解答解説

(1) は、ひし形 ABCD の面積と四角形 KLMN の面積の比較をすれば終わりです。

四角形 KLMN = ひし形 ABCD - 三角形 ANK - 三角形 BKL - 三角形 CLM - 三角形 DMN であり、辺の比から
・三角形 ANK = ひし形 ABCD × (1/2) × (1/2) × (1/2) = ひし形 ABCD × (1/8)
・三角形 BKL = ひし形 ABCD × (1/2) × (2/3) × (1/2) = ひし形 ABCD × (1/6)
・三角形 CLM = ひし形 ABCD × (1/3) × (1/3) × (1/2) = ひし形 ABCD × (1/18)
・三角形 DMN = ひし形 ABCD × (1/2) × (2/3) × (1/2) = ひし形 ABCD × (1/6)
であるので、四角形 KLMN = ひし形 ABCD × { 1 - (1/8) - (1/6) - (1/18) - (1/6) } = ひし形 ABCD × { 1 - (37/72) } = ひし形 ABCD × (35/72) となります。

したがって、
・四角柱 ABCD-EFGH = ひし形 ABCD × AE
・四角すい O-KLMN = 四角形 KLMN × AE ÷ 3 = ひし形 ABCD × AE × (35/216) = 四角柱 ABCD-EFGH × (35/216)
から，答えは (35/216)倍となります。

(2) は、四角すい O-KLMN を高さが半分のところで切っているので、点 O を含む立体は四角すい O-KLMN を (1/2)倍に縮尺した四角すいとなります。

よって、切り口の面積は四角形 KLMN の (1/4)倍となるので、ひし形 ABCD の (35/72) × (1/4) = (35/288)倍となります。

(3) は、四角形 KLMN が等脚台形で、対角線 AC に対称であることに注意してください。

等脚台形とは，平行である1組の辺(上底と下底のこと)の一方の辺の両端の内角が等しい台形のことです。このとき，平行である辺の残りの辺の両端の内角も等しく、これら以外の2本の辺の長さが等しくなります。

そこで、まず全体を ACGE で切った断面を考えてみます。

ここで重要となるのは OZ : ZX と OW : WY となります。

OW : WY = 1 : 1 となるのは簡単かと思います。

OZ : ZX は、直線 PR と AC の交点を Sと、PR と EG の交点を T とおくと、三角形 ZOT と三角形 ZXS が相似で、OT : XS = (2 + 12) : (9 + 12) = 14 : 21 = 2 : 3 なので、OZ : ZX = 2 : 3 となります。

以上のことから、三角形 OZW の面積は三角形 OXY の面積の (2/5) × (1/2) = (1/5)倍となります。

さて、なぜ三角形の面積が必要だったかというと…
・四角すい O-KLMN の体積は、辺 XY を三角形OXYの底辺としたときの高さは O-KLMN の高さに等しいので、四角すい O-KLMN = (KN + LM) × XY ÷ 2 × 高さ ÷ 3 = (KN + LM) × 三角形 OXY ÷ 3 となります。
・求める立体の体積は，辺 ZW を底辺としたときの高さは求める立体の高さに等しいので，求める立体の体積 = (等脚台形の上底 + 下底) × ZW ÷ 2 × 高さ ÷ 3 = (等脚台形の上底 + 下底) × 三角形 OZW ÷ 3 となります。

ということで、あとは等脚台形の上底と下底、KN と LM の関係です。

BD を基準に考えてみると、
・三角形 AKN と ABD が相似であることより KN = BD × (1/2)
・三角形 CLM と CBD が相似であることより LM = BD × (1/3)
・三角形 OKN と O(上底) が相似であることより 上底 = KN × (2/5) = BD × (1/5)
・三角形 OLM と O(下底) が相似であることより 下底 = LM × (1/2) = BD × (1/6)
となるので、
・四角すい O-KLMN = BD × 三角形 OXY × (5/18)
・求める立体の体積 = BD × 三角形 OZW × (11/90) = BD × 三角形 OXY × (1/5) × (11/90) = BD × 三角形 OXY × (11/450)
から、求める立体の体積は四角すい O-KLMN の (11/450) ÷ (5/18) = (11/125)倍となります。

感想

(1) と (2) はさほど難しくないので、できれば取りたい問題ですが、(3) は難しいと思います。おそらく、入試での正答率は 1% ないのではないでしょうか。

入試でなければ考えるのにいい問題ですが、入試では手を出すべきではないと思います。少なくとも去年の第5問よりも難しいと思います。