江戸時代の数学「和算」は何であって何でないのか

江戸時代の日本では、数学が子供から大人まで、殿様から町民まで楽しめる娯楽として親しまれていたという。……と聞くと「なんだなんだ、また江戸しぐさ系の作り話か」というのが平均的な令和人の感覚だろう。

現代社会の検索欄に「数学」と入力しても、予測変換に「娯楽」は出ない。一般的な人生で数学と分かちがたいのは「受験」であり、つまり立身出世の道具だ。必要であるが楽しくはないので効率的に消化したい一日分の野菜350グラム、のような扱いになっている。

そういう時代に生きていると「数学が娯楽である社会」なんてものは想像しづらいが、考えてみると「頭を使うエンタメ」は古今東西どの社会に存在する。囲碁将棋はずっと定番コンテンツだし、どのチャンネルでもクイズ番組をやっているし、大抵のバトル漫画は単なる殴り合いではなく頭脳戦要素がある。世間一般の大衆は、不要なことに頭を使うのが好きなのだ。歴史のある時代に数学がその一角を担っていたとしても、さほど驚くことではない。

たとえば江戸時代には、数学の問題を書いた「算額」という板を神社仏閣に奉納し、難問が解けたことを神仏に感謝する風習があった。フィクションに書いたら「著者の自由な想像力を評価したい」とか言われそうな奇習だが、当時の神社仏閣は現代よりもはるかに多くの人があつまる場所だった。衆目の前で「この難問解いたの俺なんすよwwwwww」とする自己顕示と言われれば、まあ納得が行く。というか自分もやりたい。

おそらくインスタ映えならぬ「算額映え」もあったに違いない。幾何問題の図形が妙にかっこいいのも多分そのせいだ。魔法陣のような模様の並ぶ算額を見せられれば、字が読めない者でも「なんかすごそうなことをやってるな」という雰囲気が出るだろう。こうした算額が、各地に800枚ほど現存している。（写真はさいたま市・氷川神社の算額、複製）

遠藤寛子の小説『算法少女』では、ドヤ顔で算額を掲げた若い武士が、居合わせた13歳の町娘に間違いを指摘されるところから話が始まる。町娘はとある姫君の算術指南役に抜擢されるが、大恥をかかされた武士の師匠が妨害工作に暗躍し……というストーリー。主人公の町娘は実在人物で、「算法少女」という言葉も彼女自身が江戸時代に著した算書のタイトルである。決して魔法少女に寄せたわけではない。

算法少女 (ちくま学芸文庫)

では当時の数学レベルはどんなものだったのだろう？　実際の和算問題を見てみよう。下図は群馬県高崎市の幸宮神社に奉納されている算額で、問題および解法は『算法勝負！「江戸の数学」に挑戦』（山根誠司／ブルーバックス）の「初級」から引用させていただいた。

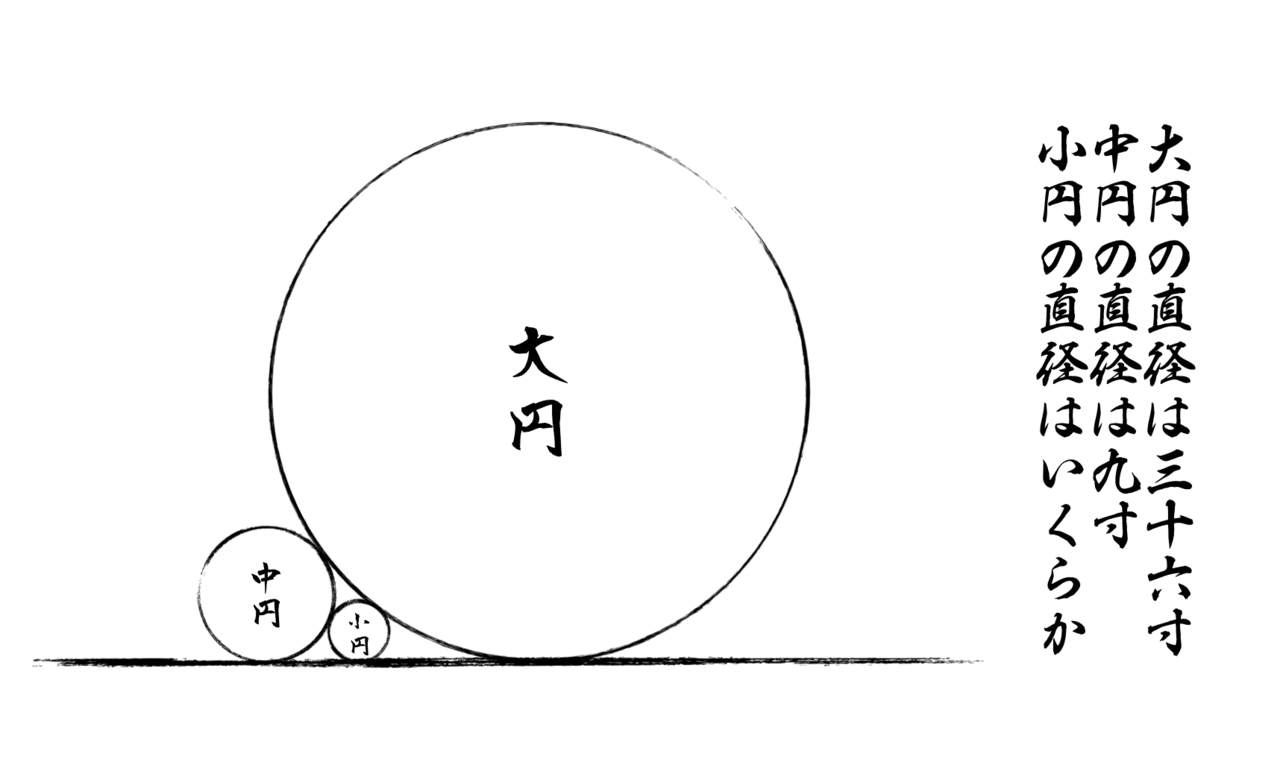
画像は私がそれっぽく作ったものである。実際に奉納されているのは漢文で「円」も旧字体の「圓」だが、数学と関係ないので現代風に書いた。

この算額が奉納されたのは文政七年（1824年）で、出題者から見れば我々は200年後の未来人だ。教育システムもはるかに発達し、9年間の義務教育に加えて高校進学がほぼ前提となっている。江戸時代の問題などチョチョイのチョイで解けるはずだ。

ことに私は数学が得意科目だったので、こうした問題をひと目見れば「はは〜ん、これは3円の中心を結べば直角三角形になるな？」と鋭い勘が働く（※ならない）。

そして小円の半径を x と置いて「え、中円の直径が9？　半径が整数にならないじゃん」と違和感を覚えながら方程式を立てて、出てきた数字がどうにも汚らしいので「ああ〜どこかで計算ミスしたのかな、受験時代はこういうの一瞬で解けたよな」などと言い訳をしながら YouTube を開いてミニ四駆をホバークラフトに改造する動画を見ながら寝てしまう。

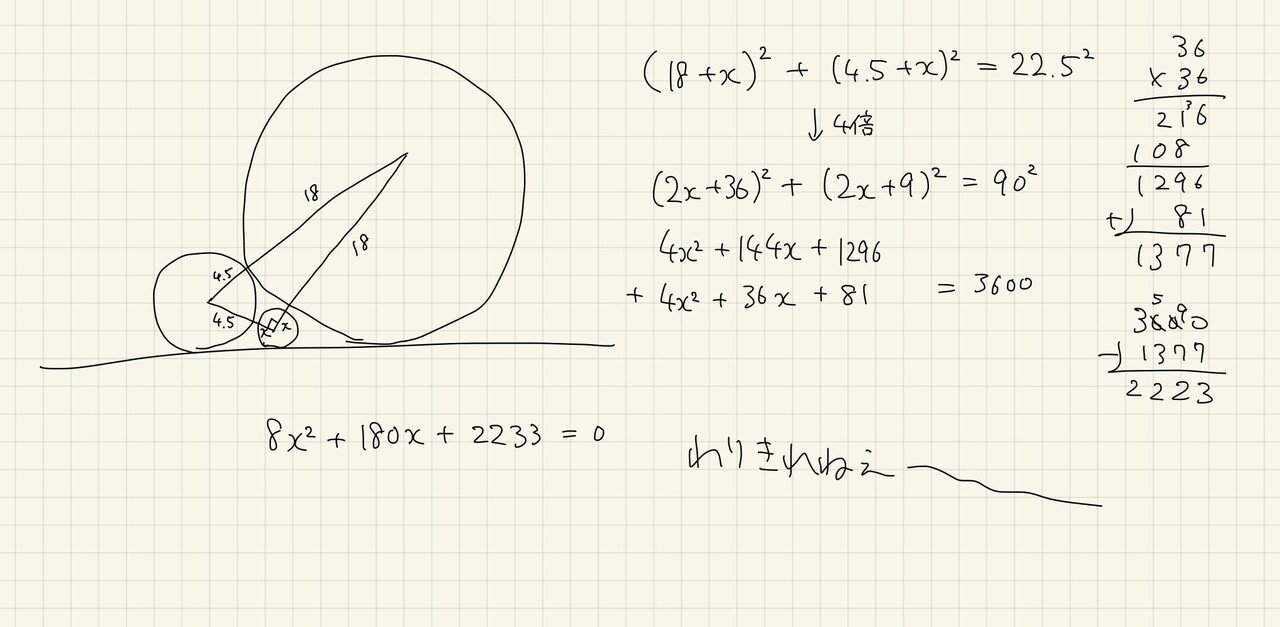
勘のいい人であれば、大円中円の直径が9、36とどちらも平方数であることに気づいたと思う。実は「直線に接する複数の円」というのは和算の頻出モチーフで、そのための公式が存在する。今回の問題で重要なのはこちらだ。

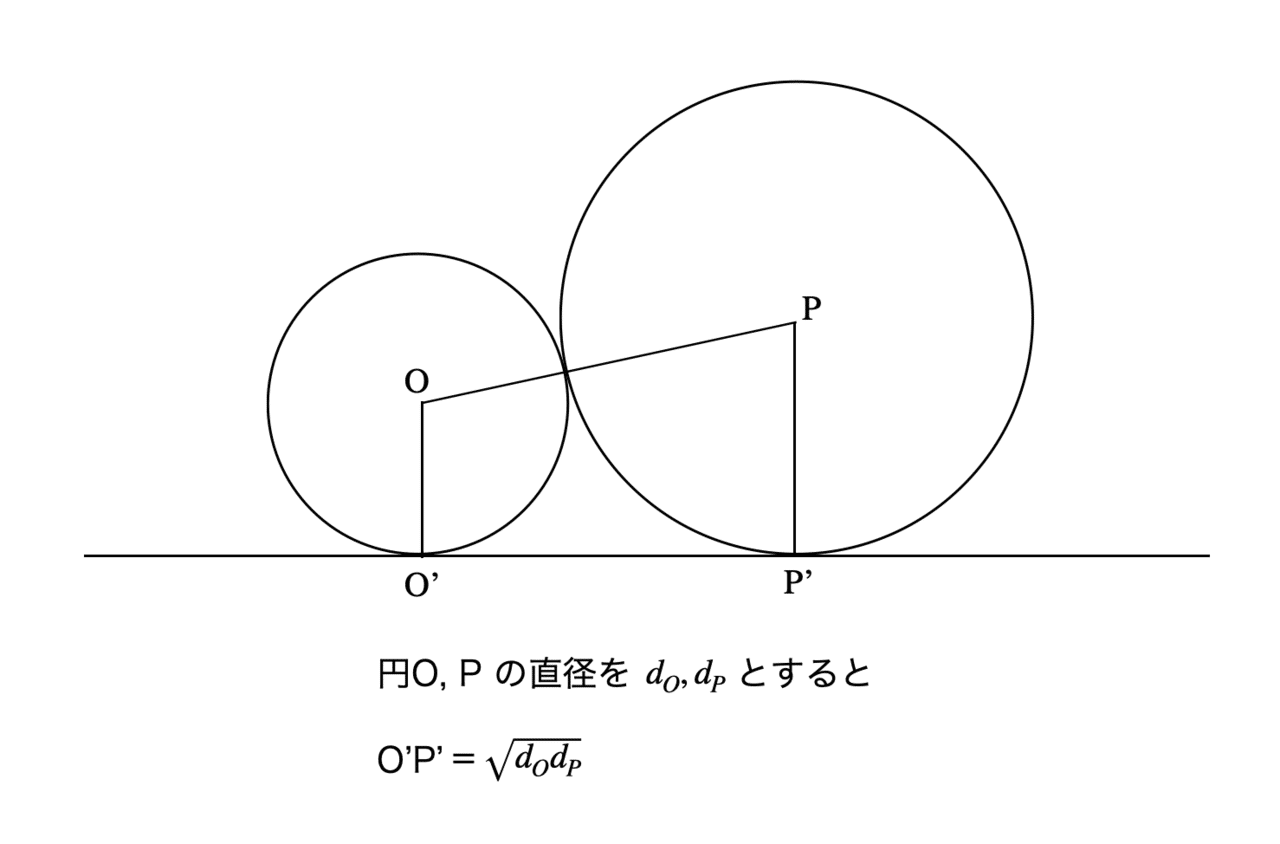
これを知っていれば、大円と中円が直線と接する2点の距離が18だとすぐわかる。同様に大円と小円、中円と小円の距離を出して、あとは方程式を立てればサクッと解ける。答えは4である。

だが、そういう解説されても「なるほど〜江戸の人はすごいことを知ってたんだなァ〜」と感心するほど私は素直ではない。「いや、そんなマニアックな公式覚えてるヒマがあったらもっと座標とかベクトルとかの概念を導入するべきだろペリー早く来い」と負け惜しみの未来人マウンティングをするだろう。

実際、和算は幾何問題が非常に多いのに、点の位置を数字で、図形を数式で表す座標幾何の発想がない。西洋数学が「定義・定理・証明」といったもので構成されているのに対し、和算はあくまで「問題・解法」が骨格になっていて、数や図形といった数学的概念を抽象化する思想が希薄なのである。（未来人マウンティング継続中）

平山諦はその著書『和算の歴史　その本質と発展』で、和算の全体的な性質を同時代の西洋数学と比較している。西洋数学はニュートンに代表されるように「自然科学を記述する言語」という側面が強かったが、和算にはそのような対象がなかったため、「問題のための問題」に終始していた、とある。（だからこそ娯楽としての地位を確立できた、という見方もできるが）

たとえば西洋数学の根幹をなす「証明」という概念は、和算においてはほとんど見られない。公理から出発し一歩一歩論理を組み立てて定理を示すということをせず、簡単な図を示して「これを見ればわかるだろう」で済ませることが多かった。

証明軽視の例として、ある和算家が西洋から中国経由で輸入された科学書を見て、「西洋は天文学や航海術が発達しているが、数学においては我が国のほうが優れているようだ。こんな直観でわかることをくどくどと説明しているのだから」などと見当違いのことを記している。ラマヌジャンだってもっと謙虚だぞ。

とはいえ、字が書ける者が稀だった近代以前の世界で庶民までが数学を愛好し、関孝和を筆頭に優れた数学者を輩出したことは誇るべきことである。ちゃんとした歴史に基づいた日本スゴイ発信をしたいのであれば和算に注目するのもひとつの考え方であるし、そのためにいっぺん数学を学びなおしてみるのもいいと思う。

などと書いてから梯子を外すと、数学を競技性のある娯楽にするのは、庶民への普及率をさておけば、わりと世界的に見られる現象である。

たとえば16世紀のイタリアでは「方程式を解く競技」というのが行われており、古代ギリシアより探求されていた三次方程式の解法がこの時代に発見されている。賭博性もある競技なので自分の解法を秘密にしがちなのだが、「絶対に誰にも言うなよ」というフリで教わった三次方程式の解法を出版したジェロラモ・カルダーノはあまりにも有名である。私は個人的に「学術において秘匿主義は悪」という信条があるのでカルダーノを支持する。