
非線形薬物の血中濃度解析① Michaelis–Menten式を克服
これまでPythonの基礎として、基本的な書き方やよく使うライブラリに関して紹介してきました。ここからは、少し趣向を変えて実務での使用を想定したプログラム作成を目指していきたいと思います。
はじめに
薬剤師の業務のひとつにTDM(Therapeutic Drug Monitoring)というものがあります。TDMは、投与された薬の血中濃度を解析し効果的かつ安全な投与設計を行う業務です。特に、治療域が狭い薬物や薬物動態の個人差が大きい薬が対象となります。
医師に診断スキルを期待するように、TDMは他職種から薬剤師が期待されるスキルの一つだと思います(※)。ただし、…計算が面倒だったりするので苦手意識をもつ薬剤師が多いのも事実だと思います。このような計算は、プログラミングのスキルでいくらでも補うことができるので、このスキルを活用しない手はないですね!
非線形薬物について
今回からのシリーズで対象とするのは、ボリコナゾールやフェニトインといった非線形薬物です。
非線形薬物の解析が厄介なのは、以下のような理由があるからです。
代謝酵素の飽和が起こるため、投与量と血中濃度の関係性が線形ではない(投与量を2倍にしたら、血中濃度は2倍以上になってしまう)
代謝酵素の遺伝子多型が知られ、代謝酵素に質的・量的な個人差が大きい(かつ、炎症などにより代謝酵素のダウンレギュレーションが起きたりもするのでカオス…)
個人差が大きいため、バンコマイシン(VCM)のように母集団薬物動態解析がしにくい(遺伝子型で分ければ何とかなるかもですが、この代謝酵素の遺伝子検査は保険ではできず、通常診療の中では遺伝子型は分からない)
VCMのように母集団薬物動態解析のソフトがあれば、1点の採血からある程度の血中濃度予測を行うことが出来ますが(あくまで、母集団に合致する患者さんの場合ですが)、非線形薬物はそうもいきません。そこで、Michaelis–Menten式を用いて解析を行います。
Michaelis–Menten式の復習
Michaelis–Menten式
詳細は教科書を振り返って頂くとして、Michaelis–Menten式は以下のようになっています。

この式を活用するためには、定数であるKmとVmaxを算出する必要があります。
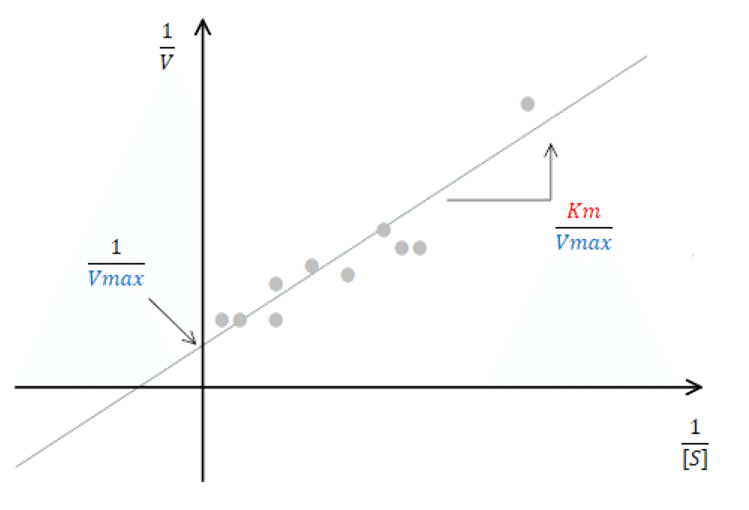
Lineweaver-Burkプロット
KmとVmaxを算出するために、Lineweaver-Burkプロットを用います。投与速度(投与量÷時間 →ここでは1日投与量と解釈してください)と基質濃度(血中濃度)の逆数をプロットし最小二乗法で回帰直線を引きます。y軸の切片が1/Vmax、直線の傾きがKm/Vmaxなので、ここから2つの定数を求めることができます。回帰直線を引くので、少なくとも異なる投与量での2点が必要となります。
血中濃度の計算
Michaelis–Menten式を血中濃度についてまとめると以下のようになります。
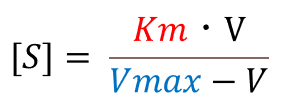
KmとVmaxは先程の方法で算出した定数なので、投与量(1日量)Vのみが変数です。Vに任意の値を代入すれば、血中濃度を計算できます。
例えば、Vに0から600までのように値を順番に代入し、算出される値(血中濃度)をプロットすれば、以下のような曲線を描くことが出来ます。

このように非線形薬物の解析には少し手間がかかります。最終的には求めた曲線からどの辺りの投与量なら有効かつ安全に投与を継続できるか検討するのが仕事になるのですが、そこに辿り着くまでのステップが遠いのです…。
投与量と血中濃度を入力したら曲線を描くところまで自動で出来たら楽チンです。というわけで次回からは、実際に非線形薬物の血中濃度解析のためのコードを作成していきますのでお楽しみに!
(※)
薬剤師のための薬物動態10の鉄則(菅野彊)からの引用です。薬剤師が薬物動態が苦手と言うのは、医師が診断が苦手と言うのと同じ意味だと先輩薬剤師に言われ(この本を紹介され)、そこからTDMを勉強するようになりました。まったくその通りだと思います。個人的には、知識やコミュニケーションスキル以前に、TDMなど他職種にないスキルをまず磨くべきだと思います。そこにプログラミングや解析のスキルが加わると、より役に立つ人材になると思います(が…マイノリティかもしれません)。

