
テストの偏差値はどれくらい変動するのか?
趣味の統計分析シリーズです。
自分の受験でもそうでしたが、子供の塾のテストや模試を見ていると、偏差値はかなり上下に変動しています。一定の期間で見たら、トレンドとしての上昇傾向や下降傾向はある一方で、短期に連続する2回で見ても、テストの成績(偏差値)は安定せずにかなり変動するようです。まるで、為替や株価のようです。
じゃあ、どれくらい変動するのだろう、ということで、基礎統計レベルの簡単な分析をしてみました。
0. まとめ
ある中学生向け難関テスト≒駿台中学生テスト(高校受験)≒駿台全国模試(大学受験)≒SAPIXのテスト(中学受験)において、連続する2回のテストの3教科偏差値の変動幅の平均は4.9である。5教科の変動は少し収束して、平均4.1となる。
難関テストの偏差値の変動幅4〜5は、学校の学力レベルで1ランクの差(公立高校1番手校と2番手校、早慶附属とMARCH上位附属、東大と京大、京大と東工大など)に相当する。
偏差値変動幅の4〜5は合格可能性の判定一つ分(20%)にも相当し、テストで判定が1つ上下するのは、平均的に起こりうることと言える。そのため、1つくらいの判定変動は気にしても仕方ない。
一方で、偏差値の変動幅が±2に入る安定ケースも一定存在する(80件/300件)。入試の合否ラインはB判定とC判定の間にあると推察できるため、A判定を取れなくても、安定的にC判定の上半分からB判定下半分に入っているなら、十分な合格可能性があると考えられる。
1. 分析対象と母集団
子供が通っていた高校受験塾の毎月のテストの連続する2回の変動が分析対象です。子供の成績だけでなく、追跡調査に掲載されている生徒のデータ(最終2回の270人分)も用いています。3教科のデータ数300件、5教科の266件が母集団となります。
毎月のテストなので、その変動は学力の伸張よりも、テストによるブレの影響の方が大きいと考えられます。データ数も300件近くあるため、学力の伸張要素は無視して、連続する2回の毎月のテストの変動は、ランダムに発生するものとして扱います。
子供の通っていた高校受験塾のテストの偏差値50が、MARCH附属高校の合格者平均偏差値くらいですです。同じレンジにあるのが、都立高校だと2番手校(戸山・青山・立川・八王子東など)、私立高校だと桐朋・城北・巣鴨あたりです。
この塾の母集団平均は駿台中学生テストの母集団平均より少し上のようですが、ほぼ同じと見なせると思います。そのため、駿台中学生テストの代替指標として扱います。
また、前回の記事で見たとおり、大学受験の駿台全国模試の母集団は、駿台中学生テストの確実圏52.7/可能形47.1くらいの高校でした。そのため、駿台中学生テストの平均層は駿台全国模試の平均層と同じと見なせます。
さらに、中学受験のSAPIXの平均層の進学先はMARCHレベルと言われているようです。この高校受験塾の偏差値表を見ると、難関私立高校(開成など)や国立附属高校は、中学受験のSAPIX偏差値表と同じくらいの偏差値帯に記載されていました。
これらを勘案すると、分析対象のテスト≒駿台中学生テスト(高校受験)≒駿台全国模試(大学受験)≒SAPIXのテスト(中学受験)として扱うことができそうです。つまり、高校受験でも大学受験でも中学受験でも、難関レベルのテストには今回の分析結果は当てはまると考えます。
逆に言えば、高校受験の標準的な模試(東京のV模擬)や大学受験の進研模試のように、母集団想定が違う平均的なテストの偏差値変動には当てはまりません。
2. 分析結果
対象データ(3教科300件・5教科266件)を集計すると、このようになりました。

偏差値の平均なので、理論的には平均値0になるはずですが、3教科で▲0.3、5教科平均で+0.2のため、多少の誤差が出ています。ただ、わずかな誤差なので、この標本(サンプル)は、母集団に近いと考えてよいと判断します。
標準偏差は3教科で6.1、5教科で5.3であり、5教科の方が変動幅が小さいようです。3教科の標準偏差6.1は、約7割の確率で、±6の変動に収まることを意味します。
右のヒストグラムを見ると、プラスの変動とマイナス変動は概ね左右対称であることがわかります。特に多いのは、中央の▲2〜0と0〜+2のほぼ変動しないデータと、▲6〜▲4と+4〜+6の±5前後の変動をしているデータです。標準偏差の約6とも一致します。
ヒストグラムがほぼ左右対称であることから、変動幅の絶対値で集計して分析することの妥当性は高いはずです。そこで、絶対値を集計したら、このようになりました。
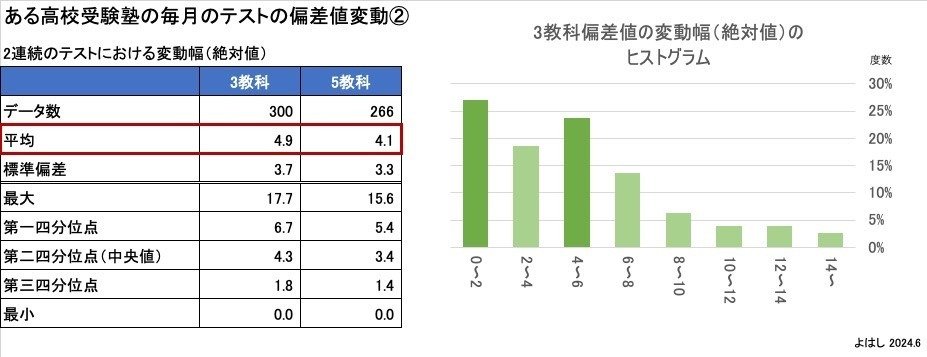
変動幅の絶対値の平均は3教科で4.9、5教科で4.1です。こちらも5教科の方が変動幅が小さくなっています。ヒストグラムを見ると、山が2つありますが、全体としては右肩下がりでいい感じの分布です。
最初のヒストグラムのプラスの変動とマイナスの変動がほぼ左右対称で、変動幅の絶対地の平均が3教科平均4.9、5教科平均4.1であることから、短期の2連続のテストでは、プラス方向でもマイナス方向でも、平均的に偏差値は4〜5は変動すると言えます。
3. 偏差値変動の平均=4〜5の解釈
次に、この偏差値の変動幅4〜5は、入試に対してどれくらいのインパクトがあるか見ていきます。
①学校の比較
東京の高校受験(駿台中学生テスト・確実圏偏差値の男女平均)で見ると、偏差値4〜5の違いはこれらの学校の差になります。確実圏偏差値は少し古いですが、2022年第5回のものです。
70前後: 筑波大駒場(72.0)、開成(69.3)
65前後: 日比谷(64.3)、早大学院(65.1)
60前後 : 国立(58.6)、明大明治(60.4)
55前後: 立川・八王子東(54.7)、中央大学(55.4)
超進学校 / 都立トップ・早慶附属 / 都立1番手校・MARCH上位附属 / 都立2番手校・MARCH下位附属というイメージです。なんとなくですが、ランクが一つ変わる印象があります。
大学受験(駿台全国模試・合格目標ライン=A判定80%相当)では、偏差値4〜5の違いはこれらの学校の差になります。合格目標ラインは2023年夏に調べたものです。
70前後: 東大・理一(68)、東大・文二(67)
65前後: 京大・工・電気電子(63)、一橋・経済(63)
60前後: 大阪大・工・電子情報(59)、大阪大・経済(60)
55前後: 九州大・工・Ⅰ群(55)、九州大・経済(56)
大学受験で見ても、東大 / 京大・一橋 / 地帝上位 / 地帝下位で1ランク変わる印象です。
これらから、偏差値の平均的な変動4〜5は、学校の学力レベルの1ランクの差に相当すると考えられます。別の記事で検証した「もう一度入試を行うと、合格者の半数が入れ替わる」という話にも通じるものがあると思います。
②模試の判定偏差値
駿台中学生テストでは、確実圏と可能圏の合格可能性の差は20%です。2022年第5回の判定偏差値が設定された1,126校において、確実圏の平均は47.3、可能圏の平均は41.2で差は約6でした。 偏差値の変動幅4〜5より少し大きいですが、ほぼ一致していると言えます。
大学受験の駿台全国模試でも、判定の違いによる合格可能性の差は20%です。A判定とB判定、B判定とC判定の偏差値の差は平均すると3〜4の幅でした。こちらも多少の誤差はありますが、偏差値の変動幅4〜5と判定1つがほぼ一致します。
これらのことから、判定の1ランク(20%)の幅と偏差値の変動幅(4〜5)はほぼ同じと言えます。つまり、テストによって志望校の合否判定が1ランク上下することは、平均的に起こりうると言えます。そのため、1ランクくらいの上下は気にしない方が良さそうです。
逆に、表1の四分位点を見ると、標準偏差が5〜6、第三四分位点が▲3〜▲4であり、偏差値が▲5よりも下がる可能性は20%くらいと推定できます。偏差値が▲10よりも下がる可能性は、分布が正規分布の場合、わずか5%です。
過去の色々な分析を総合すると、B判定〜C判定の間(倍率に依存)に、入試の合否ラインがあると推測されます(未検証)。そのため、A判定+5=B判定+10以上の偏差値があれば、ほぼ確実に合格するという仮説を持ってもよさそうです。逆に言えば、併願する安全校は、B判定が持ち偏差値マイナス10よりの学校を選べばよいことになります。
例えば、大学受験なら、東大理一志望の持ち偏差値64〜65(B判定下限)の受験生を想定します。この受験生は、早慶の理工系学部のA判定(偏差値60前半)は、不合格のリスクが平均レベルであるけど、東京理科大や明治大の理工系学部のA判定(偏差値55〜57)は、まず間違いなく合格する安全校という感じになります。
③偏差値の変動が小さいケース
これまでは、表3の変動幅の絶対値の分析から、その変動の平均の4〜5について考察してきました。一方、表2の変動値のヒストグラム(再掲)を見ると、▲2〜+2にピークがあることがわかります。中央のオレンジと青の境界のところの山2つです。

データ数で80件/300件=25%が、この▲2〜+2のゾーンにあります。おそらく、安定的に得点を稼げる得意科目があり、ケアレスミスも少ない生徒が、この変動の少ないところにいると推定できます。
先の通り、おそらく入試の合否ラインはB判定(60%)とC判定(40%)の間にあるはずです。そうであれば、偏差値変動が小さい(プラスマイナス2)の受験生は、A判定を取ったことがなくても、C判定の上半分からB判定の下半分に常に入っているなら、一度も合否ラインを割ってないと考えられます。こうした成績の安定している受験生は、個々のテストの判定(合格可能性40〜60%)よりも、実際の合格可能性はかなり高いと考えてよいと思います。
例えば、高3年の駿台全国模試の偏差値が65、63、64の持ち偏差値64で、東大理一(A:68・B65・C61・D57)を目指す受験生がこのタイプです。もし東大理一の合格最下位ラインがA判定−4=B判定−1=64の場合、この受験生の模試の判定は60%、40%、40%ですが、3回に2回は合格ラインを超えているので、合格可能性は67%くらいあると考えられます。
つまり、A判定を取ったことがあるかよりも、過去最低でもC判定の上半分を割っていないということの方が合格するかどうかの観点では大事だと言えます。
4. 最後に
大学受験でも高校受験でも中学受験でも、短期のインターバルのテストでは、偏差値がプラス方向にもマイナス方向にも4〜5は平均的に変動する、というのが今回の分析結果です。
そのため、毎月や隔月の偏差値の上下変動には一喜一憂せずに、3ヶ月や半年のスパンで上昇傾向なのか下降傾向なのかを対策を考えていくのが現実的であることが、改めて確認できました。
もし、この記事を読んでいただいた方で、受験生の保護者の方がいたら、「難関レベルのテストで、短期的に偏差値が4〜5変動するのは平均的なことだから、気にしても仕方ない」と考えてもらえると、子供の成績変動にイライラしないで済むはずです。
この記事が気に入ったらサポートをしてみませんか?
