国立難関10大学にも駿台全国模試の判定下駄はあるのか?
少し前に駿台全国模試における国公立医学部医学科(医医)の合格目標ライン偏差値(A判定80%相当)と合格者平均偏差値の差を分析しました。その際には、この2つの差のうち倍率起因差で説明できない残差を判定下駄と定義して、その推定を行っています。具体的には次の結果となり、医学部判定下駄は約3(2.6)と推定されました。
<国公立医学部平均>
合格目標ライン偏差値=合格者平均偏差値+倍率起因差4.8+判定下駄2.6
その後、この記事がこちらの掲示板で引用されていることを、ある方から教えていただきました。その掲示板ではどうやら「東大・京大と国公立医学部のどちらが難しいか」がやりとりされているようで、東大・京大派の方が定量分析の例として引用してくれたようです。
https://www.saijuken.com/kokusai/index.php?%B9%F1%CE%A9%B0%E5%B3%D8%C9%F4%A4%CE%CA%D0%BA%B9%C3%CD
私が受験の統計分析を始めたきっかけは、「雑誌やSNSで色々な憶測があたかも真実のように書かれているが、数値化されていなくて感覚論に終わっている。そうした命題を定量分析したらどうなるのだろう?」という好奇心です。そのため、上記のような掲示板の論争(?)に引用してもらえるのは、とても有り難いことです。
ただ、私の記事の記述不足もあり、掲示板での投稿内容には少し誤解をされているものもあるように思います。そこで、前回記事の補足も兼ねて、今回は難関国立10大学の判定下駄も推定して、国公立医医との比較分析を行います。
※難関国立10大学= 東大・京大 + 一橋大・東工大 + 地帝(北大・東北大・名大・阪大・九大) + 神戸大
0. まとめ
駿台全国模試における判定下駄は国公立医医では2.6あったのに対して、難関国立10大学の主要学部では0.4と推定された。年度毎の倍率変動を考慮すると、難関国立10大学の判定下駄はゼロとみなせる。
合格目標ライン(A判定80%相当)と合格者平均の差は以下のように分解できる。
<難関国立10大学の主要学部平均>
合格目標ライン偏差値=合格者平均偏差値+倍率起因差3.7+判定下駄0.4
(差の合計:4.1)
<国公立医学部平均>
合格目標ライン偏差値=合格者平均偏差値+倍率起因差4.8+判定下駄2.6
(差の合計:7.4)国公立医医と難関国立10大学の難易度をA判定偏差値で比較する際には、国公立医医にマイナス3の補正を行うのが妥当。その場合、国公立医医(例:A判定61)と補正後の難関国立10大学(例の場合58)の合格者平均偏差値がほぼ同等(例の場合54)となる。
1. 分析対象データの整備
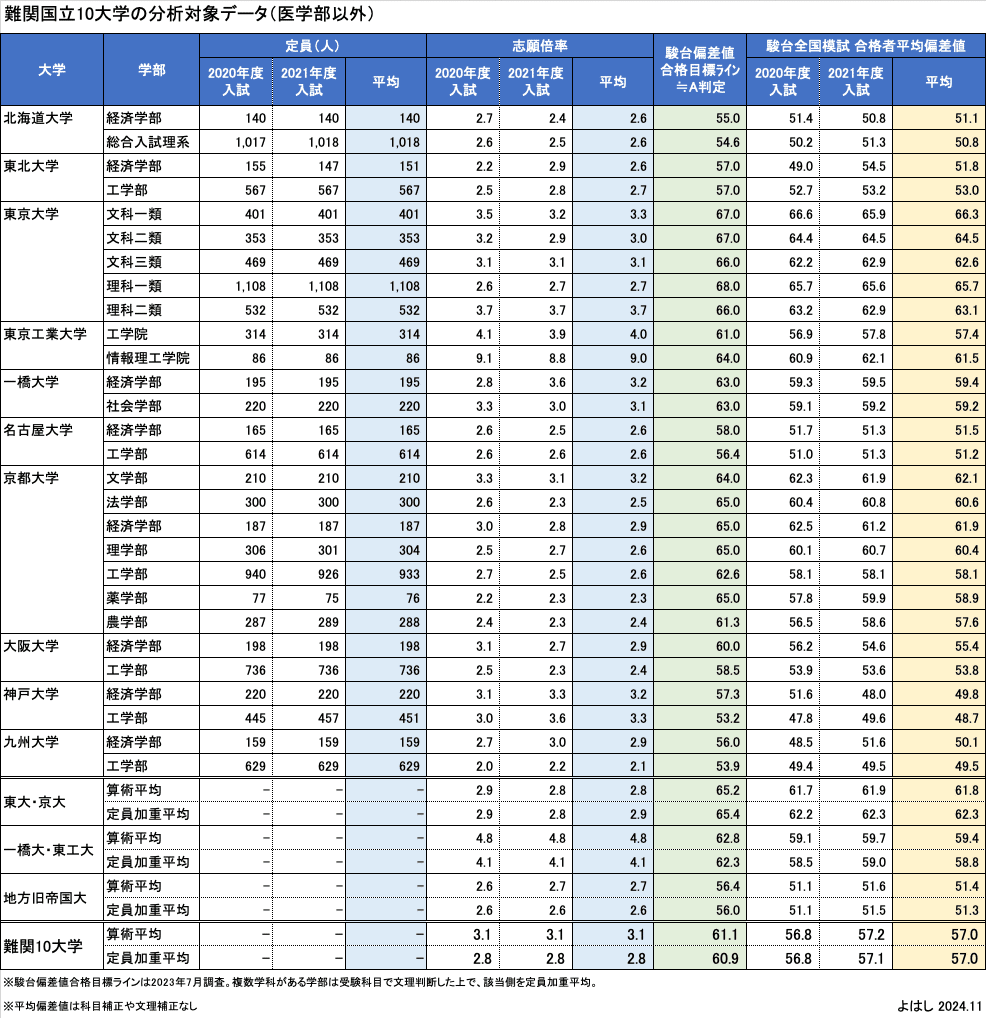
今回の分析の対象は、駿台が合格者平均を公表している学部が対象となります。具体的には2020年度入試と2021年度入試の経済学部と工学部を中心として主要学部です。
分析にあたっては、以下のデータを整備します。倍率起因差を算定する模試判定モデルの詳細は別記事をご覧下さい。
定員
2020年度入試と2021年度入試の定員の平均値を採用します。倍率
2020年度入試と2021年度入試の志願倍率の平均値を採用します。駿台偏差値の合格目標ライン(A判定相当)
2020−2021年当時のデータがないため、手持ちで最も近い2023年7月に調べた数値を使います。学部内に複数学科がある場合は受験科目で文理判断した上で、該当する学科に対して定員加重平均を計算しています。駿台全国模試の合格者平均偏差値
2020年度入試と2021年度入試のものを採用します。2021年度入試については次のWebサイトで駿台が公表しています。2020年度入試は冊子配布されていたものから引用しています。
https://www.sundai-kyouken.jp/advance/2021_vol2/data_file.html
これらのデータを一覧にするとこの表となります。
2. 難関国立10大学の判定下駄の推定
上記のデータから判定下駄を算定したのがこの表です。ポイントとなる列を順番に見ていきます。
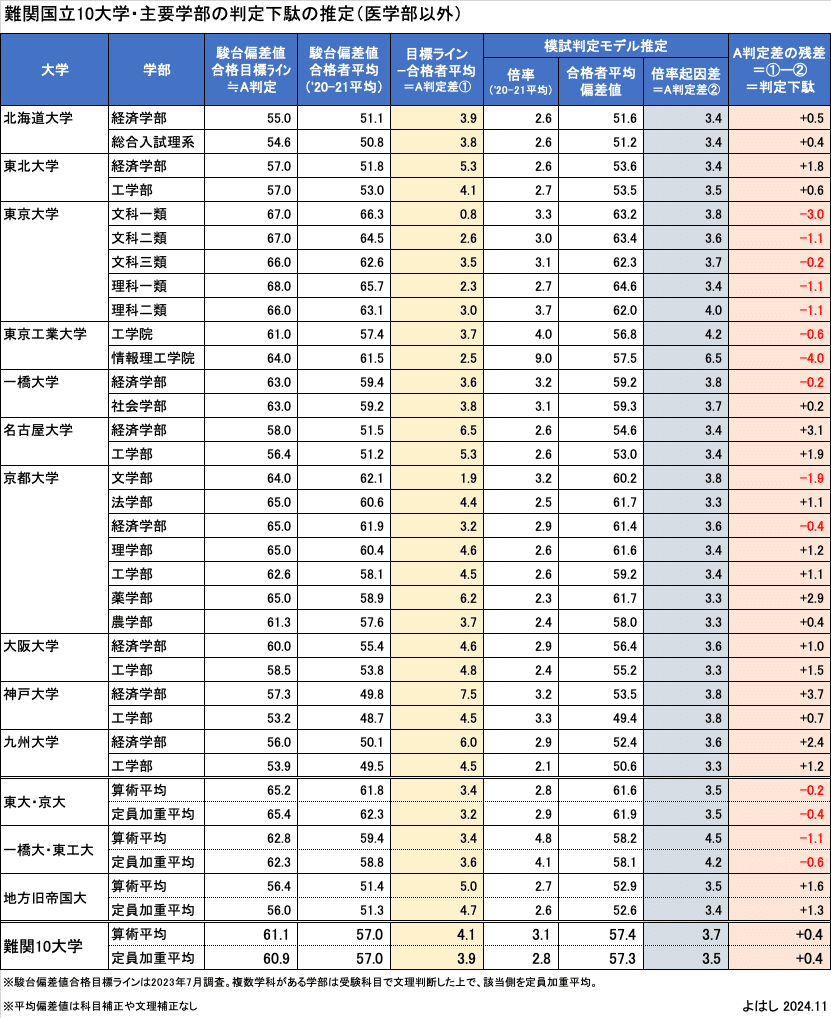
まずは、イエローの列の「合格目標ラインー合格者平均(A判定差①)」です。これは単純に合格目標ラインが合格者平均のいくつ上で設定されているかを示します。最下段を見ると、算術平均で4.1、定員加重平均で3.9であることがわかります。どちらも概ね4ですので、難関国立10大学では平均すると「合格目標ライン偏差値=合格者平均偏差値+4」で設定されているようです。
続いて、グレーの列です。このA判定差②は、受験者の学力分布と倍率に応じて合格目標ラインと合格者平均の間に構造的に発生する差を示しています。この倍率起因のA判定差②は模試判定モデルから倍率と想定分布から計算しています。この平均は、算術平均で3.7、定員加重平均で3.5となります。
この2つのA判定差を計算したのが、右端のオレンジの列です。合格目標ライン偏差値=合格者平均偏差値+倍率起因差+残差とする場合の残差にあたり、判定下駄に相当します。大学によっては逆ざやのところもありますが、全体の平均を見ると、算術平均でも定員加重平均でも0.4となります。
対象範囲の学生の平均学力を見る際には定員加重平均が適切ですが、模試の判定は学部単位(募集単位)で設定されるので、今回は算術平均の方が適切です。そこで、算定した算術平均の数値を用いると、難関国立10大学の主要学部の合格目標ライン偏差値(A判定相当)は次の構造にあると考えられます。
<難関国立10大学平均>
合格目標ライン偏差値=合格者平均偏差値+倍率起因差3.7+判定下駄0.4
(差の合計:4.1)
3. 判定下駄の評価
①判定下駄が有意かどうか
上記の分析の結果、難関国立10大学の判定下駄は0.4と推定されました。このわずかな差が有意かどうかは、本来は統計手法できちんと評価すべきです。ただ、そこまでの統計学の知見が私にはないので、やや定性的に評価したいと思います。
判定下駄はその定義(倍率起因差を除いた残差)であることから、倍率の変動によって年度ごとに変動します。今回の2020年度と2021年度の変動を計算すると、平均で0.1、最大で0.5、最小で0.0でした。
そのため、年度ごとの倍率変動バッファは0.1であり、これを除く実質下駄は0.3に縮小されます。また、倍率変動による判定下駄変動は最大で0.5あり、判定下駄を打ち消す変動をするケースもあります。
こうした倍率変動も考慮すると、全体としては難関国立10大学の判定下駄は有意ではないと言えると考えられます。
②大学グループごとの差異
表1の下段を改めて見ると、大学グループごとの集計も行っています。抜粋するとこのようになります。

これを見ると、東大・京大と一橋大・東工大では判定下駄がマイナスになっています。これは合格者平均に理論的に計算される倍率起因差を加えた後に、逆方向の補正が入ることを意味します。ただ、この逆方向の補正には何らかの意図があるわけではなく、東京一工クラスで青天井要素が大きくなると私の模試判定モデルでは倍率起因差が適切に計算されていない可能性もあります。そのため、東京一工は判定下駄=0として、倍率起因差から相殺した形で扱うことにします。
一方、地帝では1を超える判定下駄が推定されています。ただ、同等の合格者平均偏差値の一般医医の判定下駄が3程度であることを考えると、決して大きいわけではないです。そのため、ここは特段の取り扱いはしないことにします。
③判定下駄の評価の結論
上記の考察の結果、難関国立10大学の判定下駄はほぼゼロと言ってよい、と考えます。
4. 医学部との比較
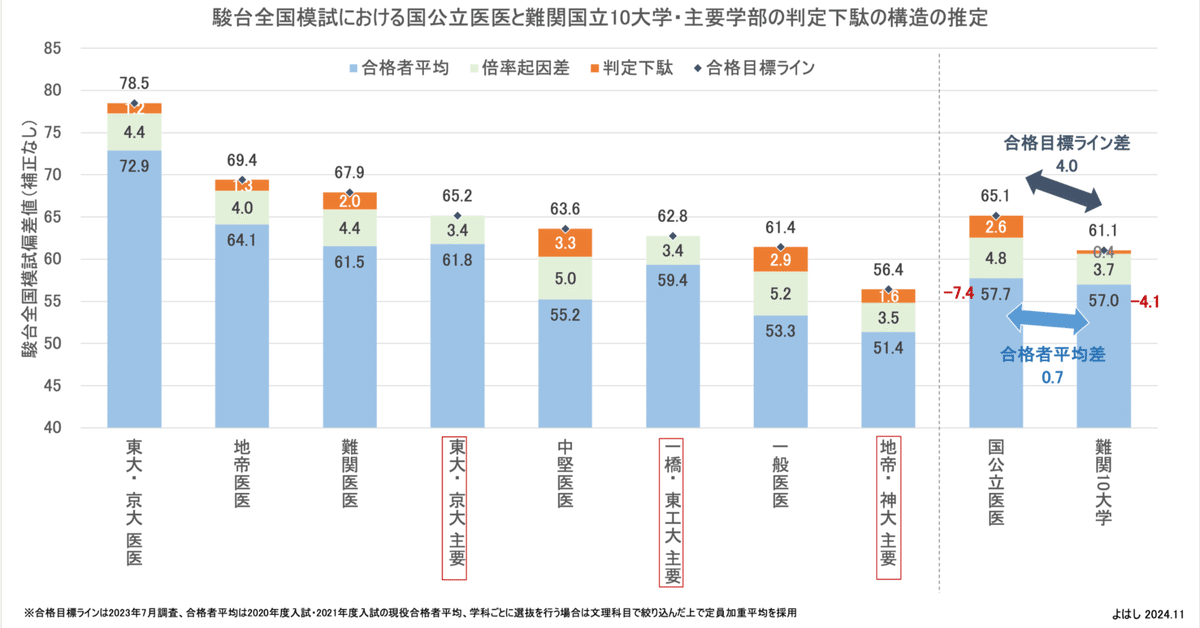
今回の分析結果を国公立医医の分析結果と並べると、この表のようになります。

比較しやすいように、合格目標ラインの偏差値順に並べてグラフにすると、こうなります。

赤枠を入れた部分が今回の分析結果です。棒グラフは合格目標ライン順に並べていますが、ブルーの合格者平均の高さを見ると、赤枠の難関国立10大学・主要学部は一つ上の国公立医医グループと同等〜逆転していることがわかります。難関国立10大学の主要学部と国公立医医は合格目標ライン(A判定偏差値)だけでは単純比較できないことが改めて示されています。
右端がそれぞれを平均化したものです。国公立医医と難関国立10大学の主要学部では、合格目標ラインでは4の差がありますが、合格者平均では1程度(0.7)に差が圧縮されていることがわかります。差し引きすると、4−1=3が国公立医医と難関国立10大学の判定の差となります。この差は難関国立10大学の判定下駄をゼロと見なす場合、国公立医医の医学部判定下駄の3に一致します。
このことから、国公立医医と難関国立10大学の難易度をA判定で比較する際には、国公立医医の合格目標ライン−3の難関国立10大学と比較するのが妥当だと考えられます。例えば、合格目標ライン61の国公立医医と比較する際には、難関国立10大学の合格目標ライン58と比較すると、合格者平均偏差値がほぼ同等になります。

5. 最後に
今回の分析で難関国立大の判定下駄も算定できました。駿台全国模試の偏差値について、改めて概算で整理するとこうなります。
<国立難関10大学の主要学部>
合格者平均偏差値=合格目標ライン偏差値(A判定相当)− 4
判定下駄:0
<国公立医医>
合格者平均偏差値=合格目標ライン偏差値(A判定相当)− 7
判定下駄:3
<国立難関10大学と国公立医医の学力比較>
国立難関10大学のA判定偏差値=国公立医医のA判定偏差値ー3
結論としては、難関国立10大学の判定下駄はゼロとして扱えるので、前回に分析した医学部判定下駄3の補正を行えば良い、ということになります。精度はどの程度あるかわかりませんが、一つの参考指標としてもらえればと思います。
