
第19話 3層のニューラルネットワークを実装する -分類問題編-
今回は分類問題に対するニューラルネットワーク(以降NNとよぶ。)を実装します。
前回は回帰問題に対する3層のNN(入力層、中間層1つ、出力層)でしたが、今回も同じ3層構造で学習していきますよ。
具体的な内容は次のとおりです。
・分類問題のNN
・全体のコード
・重みとバイアスの影響
それでは学習を始めましょう。
(教科書「はじめてのディープラーニング」我妻幸長著)
分類問題のNN
分類問題と回帰問題のNNは、次の相違点があります。
・出力層は、1つではなく複数になる。
・出力層の活性化関数は、恒等関数ではなくソフトマックス関数になる。
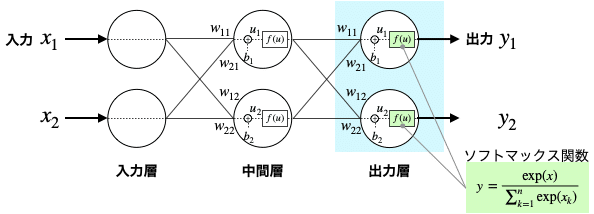
ソフトマックス関数を使えば、出力を「確率」として解釈可能になります。
例えば、犬か猫か画像診断するNNがあったとして、犬(y1)である確率70%、猫(y2)である確率30%みたいな感じです。
出力層のコードはこうなります。

全体のコード
(X, Y) = (-1.0, -1.0), (-1.0, -0.9), …, (0.9, 0.8), (0.9, 0.9)という400個のデータを入力として与え、NNで2つに分類するコードを実装してみます。
分類方法はNNの出力が2つあるので、1つ目のニューロンが2つ目より大きければ(NN図中の上が下より大きければ)、そのときの(X, Y)座標を「+」、小さければ「o」で表示することにします。
それではまずコードの前半部です。

入力信号と分類結果を格納するための箱を用意します。
そのあと重み行列とバイアスを設定し、中間層と出力層を演算する関数を定義しています。(重み行列とバイアスはあとでいじってみます。)
続いてコードの後半部です。

順伝播のコードは回帰問題と全く同じです。
NNの演算が終わったらその出力を比較(out[0]>out[1])して、分類を行なっているところが回帰問題とは違うところですね。
out[0]>out[1]の場合は(x_1, y_1)=(X[i], Y[j])として「+」で表示、out[0]<=out[1]の場合は(x_2, y_2)=(X[i], Y[j])として「o」で表示しています。
このようにNNを使って(X, Y)座標を「+」「o」に分類することができました。
今回の例題は何か意味のある分類ではありませんが、ただの二次元の数値データを「コンピュータが自動で分類できた」ということはすごいことだと思いませんか!?
重みとバイアスの影響
重みとバイアスを変えて遊んでみました。
分類のパターンがガラッと変わりましたね。

同じアルゴリズムなのに出力結果が全然違ってくることがわかりました。
つまり、NNでは重みとバイアスというパラメータの設定が重要であるということですね。
前回、今回と2回にわたって3層のNNを学習しました。
単一ニューロンより層が増えることによって、出力結果のバリエーションがグッと増えること、重みとバイアスを変化させると出力結果もガラッと変えられることがわかりました。
ですが、今回のような数個のニューロンでさえパラメータの影響がよくわからないのに、実際のNNではニューロン数は数千〜数億に及ぶそうです。
数千を手作業でパラメータ調整するのは無理ゲーですよね・・・。
でもご安心を。
我々には自動でパラメータを調整するアルゴリズム「バックプロパゲーション」という武器があるのです。
次回以降はそのバックプロパゲーションについて勉強していきます。
乞うご期待です。
それではまた(^_^)ノシ
よろしければサポートお願いします!いただいたサポートは書籍代等に活用いたします!
