
【数理的溢れ話12パス目】数聖ガウス「ムッツリスケベは濡れ衣」
以下の投稿の内容についてちょっとばかり調べが進んで、また別の景色が浮かび上がってきました。
現在、脳裏に浮かんでるのはむしろ漫画「葬送のフリーレン」に登場する「人を殺す魔法」の発展史みたいな情景…




こんな感じでさすがの「希代の天才」数聖ガウスの研究成果とて、時の流れは残酷なまでに時代遅れの存在に…
「最小二乗法」の歩んできた多難な道のり
いやむしろ、げに恐ろしきはガウスの時代以降の数学の発展速度の加速にこそあったと認識すべきかもしれません。
現代統計学は「相関係数と単純回帰(一次元関数ax+bにおける傾きaと切片bの特定)」問題を(「ハミルトンの四元数」まで視野に置いた)複素円筒/円錐座標系概念の導入によって正規分布概念と無関係に解く事も出来る(すなわちそれ自体は完全に記述統計の範囲内に収まり、推測統計の範囲まで考えを広げる必要はない)。ただしガウスの生きた時代には「ハミルトンの四元数」概念も「分散」概念もまだ存在しておらず、例えこの方面のアプローチについて何かインスピレーションを得ていたとしても、発表段階まで持ち込めなかった可能性が高い。




現代数学は、近世から近代にかけて数学者を悩ませてきた「多過ぎる連立方程式」問題を「正方でない(行数と列数が一致しない)行列は(逆行列が導出不可能なので)近似でしか解けない」問題として認識する。その解法に「ガウスの消去法」の名を残したガウスの時代に、こうした簡潔かつ適切なイメージを抱く事は不可能であったので、この方面で得たインスピレーションもやはり発表段階まで至らず終わった可能性が高い。
杉本敏夫「晩年のガウス」
最小二乗法の今と昔
1799年 ラプラスが「最小一乗法」を発表
1801年 ガウスが小惑星Ceresの軌道予測。①1801年1月1日,イタリアの天文学者Piazziが発見し2月11日まで追跡。②9月にガウスが軌道を計算て予測。③12月7日に予測通りに再発見され、その後最小二乗法を用いて軌道を精密に計算。
1805年 ルジャンドルが(メートル法制定プロジェクトの一環たる地球観測事業の一環として用いた)最小二乗法を発表(「地球の大きさと最小2乗法」)
1809年 ガウス,最小二乗法の原理を説明。①1795年に発見したと主張。②「なぜ二乗か?」をガウス分布を用いて説明。③この時「ガウスの消去法」についても言及。当然、 ルジャンドルも反論し論争が開始される。
1823年 ガウス,最小二乗法の論文を発表。ガウス分布に限らず一般の誤差分布に対する最適性を示す。
時の流れとは、げにも残酷なるもの。上で掲示した分散$${σ^2}$$と、共分散cov(R,I)と相関係数r(R,I)の関係だって、行列表現だとこんなにもスッキリ1行にまとまってしまうのです。
$$
\begin{pmatrix}
1 & r(R,I) \\
r(R,I) & 1 \\
\end{pmatrix}
=\begin{pmatrix}
\frac{1}{σ_R} & 0 \\
0 & \frac{1}{σ_I} \\
\end{pmatrix}
\begin{pmatrix}
σ_R^2 & Cov(R,I) \\
Cov(R,I) & σ_I^2 \\
\end{pmatrix}
\begin{pmatrix}
\frac{1}{σ_R} & 0 \\
0 & \frac{1}{σ_I} \\
\end{pmatrix}
$$
咄嗟に脳裏に浮かんだのが「葬送のフリーレン」におけるこの場面。

そんなガウスさんに20世紀に入ってから台頭してきた以下の質問をぶつけてみたらどんな答えが返ってくるでしょうか?
「「偏差がただ総計しただけでは0になってしまう」問題を回避する為に2乗するアイディアは、確かに平均値と中央値と最頻値が一致する状況下では無敵かもしれないが、万能とは限らないのではないか?」

実際、貧富格差分布の様に平均値と中央値と最頻値が大幅にズレるケースでは「偏差がただ総計しただけでは0になってしまう」問題を絶対値取得によって乗り越え、これと密接な関係を有する中央値を代表値とするアプローチも現れた。
また機械学習技術の発達によって新たな注目を集めつつある分布意味論の世界観においては、名義尺度しか通用しない状況下で「いかなる状況下でも必ず有効な」最頻値を代表値に取る側面がある。
あれ?もしかしたらラプラスが考案したという「最小1乗法」って「最小絶対値法」の事?
こんな質問をぶつけられたら、かの数聖ガウス様とて目を回して倒れてしまうかもしれません。「ちょっと待った!! おまいら、俺の考案した誤差関数法を人間集団への観測とか、そんなとんでもなくあやふやな対象向けに使ってるのかよ!! そんなの完全に保証範囲外じゃんかよ!! (興奮すると故郷ブラウンシュヴァイクの訛りが出たというエピソードがあるので、その感じ)」
ここからは、これまでの投稿で私が提唱してきた「1859年認識革命」史観と表裏一体の関係にある「統計革命」史観に関わってくる話となります。
ガウスが本当に欲しかったのは「手ブレ防止機能」?
前段で「(一般に推測統計や機械学習概念の大源流と考えられている)一次元回帰式ax+bの傾きaや切片bを求める問題自体は(相関係数の概念同様)記述統計の域を一歩も出ない」という話をしましたが、ならば推測統計の大源流は何処に求めるべきなのでしょうか?
機械学習自体の起源については過去投稿でこういう試論を展開。興味がある方は是非ご一読をば(宣伝)。
実は平均値と密接な関係にある(それを代表値として選択する)「偏差がただ総計しただけでは0になってしまう問題を回避する為に2乗する」アプローチには「外れ値に振り回される」という大きな問題点があったのです。そこでガウスは誤差の特徴を以下の様に捉え、その具体的数式表現として誤差関数(ERF=ERror Function)を考案したのでした。
小さな誤差ほど比較的観測され易い。
大きな誤差ほど比較的観測され難い。
従って、一定以上の誤差を切り捨てる事によって観測精度(Observation Accuracy)を確定する事が出来る。
$$
erf(x)=\frac{1}{π}\int_0^xexp(-x^2)dt
$$

後世の人間はこの「値域が0を中心に-1から+1にかけて分布する」式を確率論で扱う「0から1への分布」に変換する為に1を足して2で割りました。式の見た目はまるで同じ。ただし誤差関数は(上掲の操作の影響で?)分布の中心「平均0、分散1」ではなく「平均0、分散$${\frac{1}{2}}$$」の位置に写像されます。
平均μ、分散$${σ^2>0}$$と置いた場合の累積分布関数(Cumulative Distribution Function)
$${N(μ,σ^2)=\frac{1}{2}(1+erf \frac{x-μ}{\sqrt{2πσ^2}})}$$

この累積分布関数(Cumulative Distribution Function)を微分すると得られる確率密度関数(PDF=Probability Density Function)がいわゆる「正規分布のベルカーブ」通称「ガウス分布」。そう、こんなところにもガウスの名前が…
平均μ、分散$${σ^2>0}$$と置いた場合の確率密度関数(PDF=Probability Density Function)
$${N(μ,σ^2)=\frac{1}{\sqrt{2πσ^2}}exp(-\frac{(x-μ)^2}{2σ^2})(x\in\mathbb{R})}$$

なんか添字部分とか複雑化してますが、これは「平均μ」「分散$${σ^2>0}$$」の二つのパラメーターを用いて全体を眼前の観察対象の分布に容易にフィッティングさせる為の工夫で、最初にその仕組みを知った時の「サイボーグ恐竜みたい」という第一印象が私の中では今なお根強く続いていたりします。何しろ本体は(少なくともガウスが大元となる誤差関数を考案した時点では)有名な「ヴェーバー‐フェヒナーの法則」同様「(それまで蓄積されてきた相応量の経験則に基づくとはいえ)全く数理的根拠を有さないただの仮説」に過ぎず、ある意味現在なおその状態が続いているという…

中心極限定理そのものは一応「近代に入ってから数学的に証明された」とされているが、そういう話はあまり知られておらず(誰の関心も引き寄せない)「証明されているかどうかは現実の普及史と無相関」という辺りにこの問題の奥深さがあったりする。
中心極限定理の歴史
実際には自然のあらゆる事象において観測されるので、最終的に人類の多くは「少なからぬ確率分布がサンプル数を無限に増大させていけばこの分布に収束する」という考え方を受容しましたが、もちろん例外はあるしガウスが生きていた当時は、まだまだ「この世界のあらゆる事象には、それぞれ神が定められた固有の収束確率が存在する」なる伝統的考え方が根強かったので(それに逆らったベイズ統計は徹底的に叩かれた)、ガウスは自分の考案した数式についてのこうした可能性について一切語らず、複素数概念についても同様の傾向が見られるのをこの投稿シリーズでは「ガウスのムッツリスケベ」なるキーワードで対象化してみた訳です。
ガウス ( 1777 年 - 1855 年 )
ところで、この様な「正規分布概念の浸透」は世にいう「統計革命」史観の一側面に過ぎません。もう一つの重要な側面、それは「統計の対象が天体や自然現象の様な対象を単一に絞れる物理現象だけでなく生物や人間の集団の様な無数の個体で構成される群に推移した」点でした。「ガウスが目を回して倒れてしまう」とはまさにこのパラダイムシフトを指したもので、実際ガウスの時代の感覚では「あんな状況に左右され過ぎて、収束すべき平均も分散も見定められない対象に、そもそも統計学的方法なんて使えるの?」ではないかと思います。ガウスは政治的には頑迷なまでに守旧的な王党派で、共和主義には嫌悪感を抱いていた様なので余計にそう感じる側面も。



ただしガウスは「ムッツリスケベの人」でもあった訳で、多少そういう発言があったにせよ王侯貴族や教会上層部の様な伝統的インテリ=ブルジョワ=政治的エリート階層のパトロネージュなしには科学者や芸術家の暮らしが成立しなかった時代のポジション・トークとして差し引いて考えるべきとも。ちなみにガウス自身は投機活動で相応に蓄財し、資産運用コンサルティングの分野にも造詣が深かったのか「未亡人救済の為の保険金運用論」なんて論文も残していたりするかなりの俗物なので、それほどパトロンの視線を気にしていた風でもない?
ガウスと生命保険数理について
こうして全体像を俯瞰してみると、ガウスが中央極限定理や誤差関数に拘泥したモチベーションは「(天文学者にとっての主敵の一つたる)手ブレを可能な限り排除したい」なる思いだった情景が浮かび上がってくる訳です。

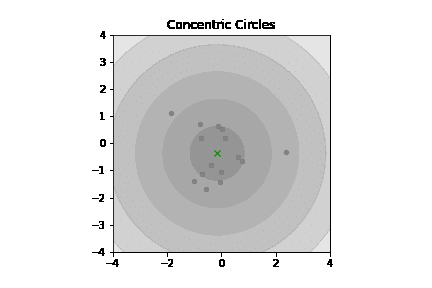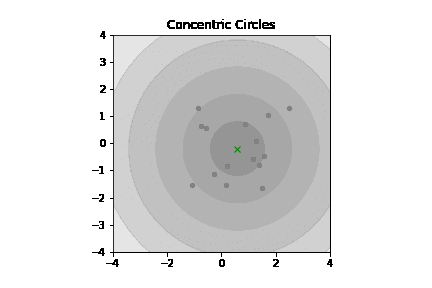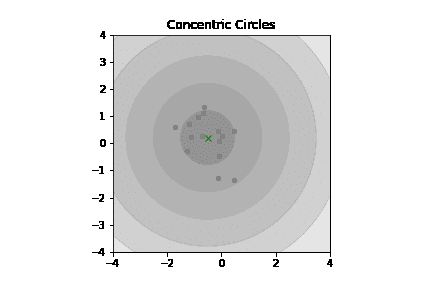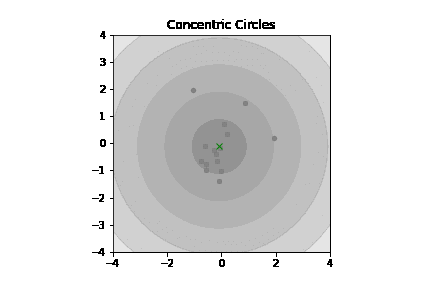

あらかじめ「明かな外れ値」を除去する事が可能なら「分布の収束」がさらに早まりますね(すなわち、より少ないサンプル数で相応に信頼可能な観測結果に到達可能)。こういう目的の為に誤差関数自体は考案され、統計学の世界は記述統計から推測統計の世界に最初の一歩を踏み出したという次第…
「統計革命」第二波
19世紀後半に入ると統計学がこの様に「天体や自然現象の様な不動の対象」のみを観測対象とするだけでは済まなくなっていきます。そしてその過程では、欧州における産業革命の浸透が重要な牽引役となりました。そう、大量生産と大量消費のスタイル普及を背景として「庶民」が経済活動の主体として重要な役割を担う展開を迎えたのです。とはいえ、そんな時代にあってもあくまで伝統的価値観を墨守しようとする守旧派インテリ=ブルジョワ=政治的エリート階層出身の有識者層による抵抗は根深く、これに新興階層を形成した庶民の保守派も加担。こうした攻勢の矢面に立たされたのが「なまじ有用だったが故にムッツリスケベを通せなかった」ベイズ統計だったりした次第。
ベイズの法則は理論家たちの懐疑的な目を逃れてあちこちの狭い隙間にぽこぽこと湧き出し、実践家たちが証拠を評価し、多種多様な情報を組み合わせて自分たちの知識の溝や不確かさを克服するのを助けていた。
理論家の非難と実践家の有効利用のこの裂け目に向かって行進したのが、政治力のある数学者ジョセフ・ルイ・フランソワ・ベルトラン率いるフランス軍だった。ベルトランは、無数の不確定要素に取り組む砲術担当の佐官級将校のためにベイズの法則を仕立て直した。砲兵隊は敵の正確な位置や空気の密度や風の方向、さらには手作りの大砲に生じる誤差や射程や方向や発射物の初速といった不確定要素と向き合わねばならなかった。
砲術の将校たちはベルトランの厳密な基準にしたがって、同一の工場、同じ条件の下でほぼ同じ職人が同じ材料を使って同じ手順で作った大砲に限って等しい確率を割りふるようにした。こうしてフランスやロシアの砲術将校たちは1880年代から第二次大戦までの約60年、ベルトランの教科書を参照して大砲を撃ち続けたのだった。
そう、当時最初に統計革命の先頭に立ったのはまさに近代化された軍隊と都市計画を推進する国家だったのです。そして英国においてその先頭に立ったのが「クリミアの天使」なる美名だけでなく「ミス軍務省」なる恐ろしげなあだ名でも知られた「統計学とプレゼンの母」ナイチンゲールだったという次第…
ここまでで既に十分な長さに達してしまったので詳しい話は別投稿に譲る事にしましょう。ここでは「統計革命」第二波においては上掲の文章に垣間見られる「不確かな領域だからこそ確かな統計が求められる」ジレンマが存在し、まさにその状況下において分散概念を中心とする「正規分布概念を中心に据えた推測統計」や最尤推定などの概念、t検定や分散分析の様な「平均をめぐる推定」の概念が次々と開発されていった事を指摘するだけに留めます。
AI生成画像における「自我同一性」問題
ところで上掲の様な「カメラの手ブレ」あるいは「卵子に精子が群がっている」様な映像を見慣れていると、どうしても仲間に含めたい最新情勢があります。マルチモーダル機械学習の最先端、連続AI生成画像がそれですね。




昨年時点でのネットにおける拾い物。上掲の様にこれまで私は分布意味論の世界は原則として「(頻度しか代表値に選び得ないほど茫漠とした)名義尺度の世界」を対象とするものと認識してきましたが、ここでは特定の観測対象がそ自我同一性を保ちつつ「有意味な連続移動」を達成しております。この技術はこれからどういう方向に向かうのでしょうか?
ただしこの話に触れるにはまだまだ準備が足りません。そういう現状が確認出来た時点で以下続報…
この記事が気に入ったらサポートをしてみませんか?
