
【とある本格派フェミニストの憂鬱9パス目】科学的実証主義以前の世界=博物学や呪術論の世界?
以下の投稿の続き。

前回投稿段階ではメカニズムが良く分からなかった「どうして私のTwitterおすすめに流れてくる(エロ)画像生成AI投稿に流れてくる少女達の服装と、実際に路上で観察される少女達の服装はここまで出自が異なるにも関わらずどうしてその内容が部分一致するのか?」という疑問に対して幾つかの答えらしきものが得られました。
①そもそも「裸を見せてください」なる率直なオファーに素直に「はい」と答えないのが婦人服の出発点。そういうこの駆け引きのどこかに通底するものがあるのは当然の事。
白無垢なので目立たないが、こうして長年に渡って鍛え上げられてきた「女性が男性の視線を翻弄し抜く技術」の集大成が花嫁のウェディングドレスのデザインだったりする。
②大規模言語モデル(LLM)にどういうプロンプトを与えるとどういう画像が安定して得られるのか見定めるのは本当に難しい。それでTwitterおすすめに流れてくる(エロ)画像生成AI投稿の多くは、この方面に秀でた「プロンプト職人」の研究成果を流用しており、この人達の血の滲む様な努力が現実のファッションとの乖離をある程度まで防いでいる。
まさしくこの世界…


この構図は2000年代にPoserがブームになった時も確実に存在しました。手持ちのポーズ作品集の内容をひたすら打ち込み続ける「ポーズ職人」や、様々な実在する服や小物を打ち込み続ける「小物職人」果ては「ドイツに実在するブルネットの髪色は500種類を超える」と豪語し、その全部を提供した「髪色職人」なんてのまで。特に絶大な人気を誇ったのがプロの証明セットを再現して配布する「照明職人」で、こうした人々が全体としてのクオリティ向上を支えていたのです。現在の画像生成AI投稿界隈は、とにかく「出したい絵を安定して出す」のが精一杯で、まだまだそういう分業化はなされていませんが「ありえる未来の一つ」として参考まで。ただし技術的背景があまりにも違い過ぎるのでコミュニティ構造は相似しても現れ方は全く別物となるかもしれません。さらにいうと、ここでいうPoserコミュニティは
仕様の度重なる激変
Dazの様なマネタイズ可能な市場の登場
などの影響で篩に掛けられ自然消滅。現れて間もない「画像生成AI投稿界隈におけるプロンプト職人を中心とするコミュニティ」については、こちらの道を辿る可能性もある事を忘れてはいけません。
③大規模言語モデル(LLM)だけに現実世界とのリンクはデフォルトで十分に出来ており、特にプロンプト指示がない箇所ではそれが出力されている。
上掲引用にあります様に、今年リアルの少女ファッションでは5月のコロナ明けを契機に6月以降「生足はいてない系」から「ハイウェスト/ハイライズ」系への激変があった訳ですが、これなどが(プロンプト職人などが特に支持を出してないにも関わらず)ちゃんとそれなりには反映されたりしてるのですね。
一方「シフォンドレイヤースカート」や「ダンサースリットスカート」の様に、巷でそれなりに流行してるにも関わらず画像生成AI界隈に全くといっていいほど登場しません。
どうやらそもそも大規模言語モデル(LLM)の「餌」となる元画像を二次元絵師が生成しておらず、ネット通販サイトのカタログもロングテール戦略を用いて「売れ筋だけが売れる宣伝を忌避している」為に「餌」としての役割を果たしてないのが原因である模様…
実は今回の分析に取り掛かる以前からそういう側面には気付いていて、もっと大規模言語モデル(LLM)寄りの原因じゃないかと勝手に考えていたのですが、実際に調べてみるとそうでもありませんでした。そしてむしろ逆に強く意識する様になったのが「女性スタッフが多数参加し、女性ファンが多いとされ(諸説ある)、実際そこで取り上げられる女性ファッションも現実との連動性が高い」アイドルマスター系の、まさにその部分を画像生成AI投稿界隈に巻き込めていない事による機会損失。
なお、路上観察結果との一致度でいうと来年アニメ化する少女漫画「指先と恋恋」がかなり高かったりします。ヒロインがネット通販サイトを物色してる場面があり、おそらく作者もそうであり、そういう部分がそういう形で反映しているのだと思われます。ただし、少女漫画なるもの何十年にも渡って読み続けられるものなので、そこまで今のファッションに連動する展開が吉と出るか邪と出るかは、また別問題…
なお、私が路上観察結果から検出したのは「量産型女子」だった可能性…
④夏頃の接触冷感レース使用製品のラインナップ変遷を眺めるうちに思いついたのだが、もしかしたら若い女性向けのネット通販サイト、単なるロングテール戦略だけでなく「多数のバリエーションを製造して並べ、次の製造に際しては実際に売れたタイプのバリエーションのみで埋める」ある種遺伝子アルゴリズムを用いているのかもしれない。
その結果として思わぬシンクロニシティが起こってる可能性も。例えばこんな「色パカ」スカートも、そういう遺伝子アルゴリズム探索の結果と大規模言語モデル(LLM)のランダムウォークの結果が重なった産物としか思えない。
⑤私は今回の分析を直接、大規模言語モデル(LLM)にプロンプトを打ち込んで得た訳ではない。それは優秀なプロンプト職人に援用された優秀な(エロ)画像生成AI投稿者の投稿を私が選好し、なおかつTwitterシステムそのものがそのフィードバックを受けて最適化したデータセットなのだから「私が見たいもの」が得られたのは当然といえば当然の話に過ぎない。
初めから分かっていた事ですが、こういう構造になってる為に私のこういう観測結果は第三者が客観的に(方法論だけ継承して無作為に試みて)再現可能なものではないんですね。それでは何でこういう試みを始めたのか?もっと根底にある問題、例えば「分類とは何か?」といった考え方についてのヒントが得たかったからで、やっとその準備が整ったという感じ。
そもそも「分類」とは何か?
機械学習論におけるこの問いの答えは明白です。二次元的には「ある分布を、任意の峻別線を引いて2分する事」「この峻別線がもし直線だったら 、傾きaと切辺bの組み合わせax+bで表せる線形回帰(Linear Regression)となる」。この時、この分布の各元は特定の数直線上に順序尺度(Ordinal Scale)に従って一次元に並べ直される事になるのです。
「二次元→一次元の次元削減が達成された」という訳ですね。主成分分析などは、これをより高度なレベルで達成する分析技法となります。
数学では一般にA>BとA>Bの場合の中間としてのA=Bの場合を意識しますが、分布論は確率論同様「面積」で考えるので「分布幅0の直線」に分布中の元が重なる確率も0と等しくなります。
なお今回の分析では暫定的にざっくり「仕草(上半身、下半身)」「服飾(上半身、下半身)」と直行二次元を切っています。この場合にはどうしても「(ジャンパースカートの様に)ボトムスとトップスが連続する服」「(跳躍の様な)全身動作」が出てきてしまうので峻別線の分布はどうしてもゼロにならないという事になりますね。まぁこの辺り、今回の分析では別に支障とならないのでとりあえず放置状態という…
一方「分類」が死活問題となる局面も存在します。




例えば精神医学の分野においては、人間は現実を現実と認識する(空想と区別する)為に現実検討(Realy Testing)能力を備えている必要があるとされ、これも分類の一種といえば一種。人間は「世界そのもの」と直面する事が出来ない為、五感で実感される感覚的世界と観測主体たる自分自身を結びつける為に相応の世界観に裏付けられた「現実感」を保たねばなりません。これが壊れた一例が統合失調という訳で、まず最初に当事者に「自分を支えてる現実感が壊れている」という認識がない事が問題となる訳です。
そういえば「分類の感覚がしっかりしている事こそ人間が人間でいる為の条件」という話なら、こちらでもしました。
(自動車廃止論者の考え方も)ヴィーガン過激派の考え方も基本構造は同じ。「誰かに実害を与える」も「誰か」の規定部分に根本的欠陥があるとしか思えません。
ポーランド人作家スタニスラフ・レムのSF小説「ソラリスの陽のもとに(Solaris,1961年)」では、惑星生命体ソラリスの見せる幻覚のせいで見る事聞く事全て信じられなくなった主人公が、自分がまだ正気かどうか確かめるべく高度な軌道計算に取り組みます。現代人の正気を担保しているのは科学実証主義で、惑星生命体ソラリスはこの基底を脅かしてくる存在なので人類の手に負えないという構図。ロシアの名匠アンドレイ・タルコフスキー監督の手になる映画はこの部分をバッサリ改変し「結局のところ、誰にとっても自分が信じたものが現実なのだ」みたいな三文ドラマ的結論に落とし込んだので随分とお冠だったとか。確かにスタニスラフ・レムが本当に語りたかったであろう「確かに科学実証主義にはあらゆる疑問に答えを出せる様な融通性はないが、それでも人類が先史時代から探し続けてきた「正気を保ち続ける為の手段」としてはまだマシなレベルである」といった真摯な科学的メッセージの映像化が難しい事は認めざるを得ません。
それでは科学実証主義以前の時代まで遡る「人類が正気を保ち続ける為の手段」とは? まず真っ先に思い浮かぶのが「伝統的な呪術的世界観からの脱却を目指して始められた」博物学(Natural History)や本草学の世界。
かつて「人類が正気を保ち続ける為の手段」だった何かとしての呪術
以下の投稿でも指摘しましたが、今回の分析で私が直面したのはまさにそういった次元の問題だったのです。
というより、私のアプローチそのものが呪術へのマルセル・モースのアプローチ的とも? そういえばマルセル・モース「呪術論」解説に「モースはありとあらゆる身体動作に歴史的に与えられてきた呪術的意味合いを解説する百科事典の出版を計画していた」なるエピソードが紹介されていましたが、まさにそれを地でいく展開…
「モースの呪術論について。あるいは呪術の全体的社会的還元について」
ところで、ここでいう「しっかりした現実」とは何でしょう。数学的にいうと「全微分が掛かる=分類不能の残余を切り捨てて良くなり(0とカウント可能する事が許されて)閉世界仮説が成立する」概念に該当しそうな気がします。
数値演算につきものの「今回はこの辺で勘弁しといてやる」的なアレ。これが出来ないと人間は無限の杞憂に悩まされ続ける事になるのです。
その点、大規模言語モデル(LLM)は、それまで人類が「いかなる分布も無限に積み上げ続ければ正規分布に回帰する」としてきた領域において、しかも不偏分散と標本分散を区別する意味が消失する「サンプル数3000の壁」のさらに向こう側「パラメーター数$${2^{10000}=10^{30}}$$以上の世界でパフォーマンスを向上させる」というのですから、とんだ惑星ソラリスもあったものです。
このシリーズの投稿で最初から使ってきたこの表を思い出してください。
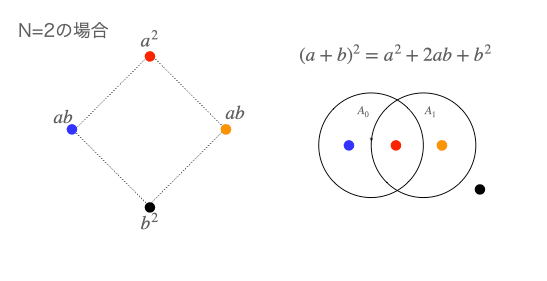
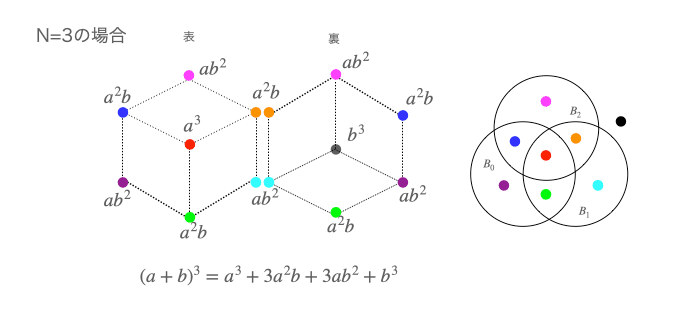
カンブリア爆発期に生物が備えた視覚と視覚情報を処理する脊髄の末裔を使って考える人類にはこれより高次元の世界はイメージ出来ないので、次に思い浮かべられるのはこうした展開の極限に現れる円環/球表面のみ。

そこでは「円環もしくは球表面上の任意の点は中心から伸ばされた垂線と垂直に交わると同時に微小隣点と水平に交わる」といいますが、この2点間の理論上の距離たるや$${\frac{1}{\tilde{∞}}}$$という有様。ここで飛ばした中間領域に有用性が生じたと突然言われても、本当に途方にくれるしか…

しかも話は最初から「全微分が通れば問題解決」という内容ではありません。画像生成AIの生成した画像で説明を試みましょう。以下が「全微分が(ほとんど)通った」状態。



服装誤差は間違い探しレベルで、概ね「被写体としての同一性」が確保されています。画像生成AIの特徴を考えると物凄い技術ですね。ところで概ね「全部分が通る」は解析の出発点に過ぎず、ここからそこでは定数として扱った各変数の振る舞いを調べる偏微分の特定が始まる訳です。



さらに物凄い技術。「被写体としての同一性」を維持しながら「撮影場所」を移動させ、見事に散歩感を実現しています。こうした方法論を駆使して人類はあらゆる技術を進化させてきた次第。私の今回の分析も、最終的に目指しているのはそういう領域だったりする訳です。


ついでなので、よ具体的に計画を記しておきましょう。今回の分析は最初から「男子から女子へのある種の限定的アプローチ」に終始する事が明らかだったので、これに「女子側の諸事情」を対比的に添える形で全体像を完成させる予定になっております。果たして年内にそこまで持ち込めるでしょうか? まぁ、今こう記しておいて、後で読み返すのもブログの醍醐味というもの。
そんな感じで以下続報…
