（メモ）ロバストｚスコアを用いた異常値の除外

外れ値を検出するスミルノフ・グラブス検定について調べていて、正規分布していないときはどうするんだろうという疑問を抱いたところ、四分位範囲を用いた「ロバストｚスコア」を使う方法があることを知りました。

普通箱ひげ図を書く場合、第３四分位数から第１四分位数を引いた値である四分位範囲IQR（interquartile range）を用いて、外れ値を決めます。
第３四分位数に四分位範囲の1.5倍を足した値以上を上側の外れ値、第１四分位数から四分位範囲の1.5倍を引いた値以下を下側の外れ値とする方法です。

これは平均値と標準偏差を使用するスミルノフ・グラブス検定にくらべると、外れ値の影響を受けにくいロバスト（頑強）な方法です。

これとは別に、四分位範囲を用いてデータを標準化するロバストｚスコアを利用する方法が、ここでメモしておくものです。
平均値の代わりに中央値、標準偏差の変わりに正規化四分位範囲（normalised IQR, NIQR）を用います。

四分位範囲を標準正規分布の確率変数に対応させると、Ｚの確率分布関数をＦ（ｚ）で表すと、F(0.75) - F(0.25) = 1.3489となります。

ここから、正規化四分位範囲は、

で求めることができます。データが完全に正規分布をしている場合、四分位範囲は標準偏差×1.3489で求めることができますから、このとき正規化四分位範囲は標準偏差に一致します。また、当然ですが中央値は平均値と一致しています。

このことから、中央値を平均値の代わりに、正規化四分位範囲を標準偏差の代わりに用いて、データを標準化することができることが分かります。

つまり、i番目のデータのロバストｚスコアは以下の式で求めることができます。

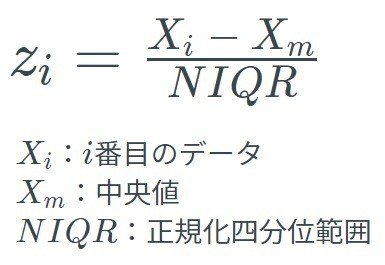
平均値と標準偏差を用いた標準化得点ｚを用いた外れ値の検出では、2または3つまり平均値 ±標準偏差の２倍または３倍を基準とすることが多いです。たとえば、z=３以上であった場合、そのデータは平均から「標準偏差×３」以上かけ離れており、全体の99％分布内に収まらない値と考えることができますから、これは相当平均からかけ離れた値と言えます。

ロバストｚスコアでも同様に2または3を基準とすることが多いようです。化学分野や工業分野では、このロバストｚスコアによる異常値の棄却がよく行われているようです。

冒頭の四分位範囲による外れ値の検出ですが、データが完全に正規分布をしている場合、第１四分位数および第３四分位数は平均値±標準偏差×0.67ですから、外れ値の基準は平均値±標準偏差×2.70となります。標準化得点zでは平均は0、標準偏差は1ですから、外れ値の基準は絶対値2.70となります。
よって、ロバストｚスコアによる異常値の棄却で、絶対値2.70を基準とすれば、冒頭の四分位範囲による外れ値の検出とだいたい同じ基準ということになります。

しかし、この外れ値というのは分野によって考え方を変える必要があります。工業的な統計の場合、求められているのは「均一かどうか」という場合が多いですから、検定的な異常値の棄却は意味があります。しかし、医療の分野ではそもそも人というばらつきのある存在が対象ですから、検定的な異常値の棄却は馴染みません。医療的にありえないデータか測定ミスの可能性があるデータ以外は除外しないのが基本となります。

【参考文献】

・井口豊(2012-)「ノンパラメトリックな標準化Ｚ変換：中央値と四分位を利用したロバストzスコア」
・和田かず美(2010)「多変量外れ値の検出 ～MSD法とその改良手法について～」統計研究彙報67(4)
・保母敏行ほか(2008)「日本分析化学会における標準物質の開発」分析化学57(6)