高校物理のための微積分

高校物理では色々な数学を使います。
中でも重要な概念が微積分。
本来は高校2、3年生で勉強する内容ですが、早めに触れておいても損はないはずです。
未習の人や苦手な人のために、簡単に紹介します。

※よく分からなくても、とりあえず流し読みしてください。何回か読めばきっと分かると思います。

微分とは

微分とは、簡単に言えば「変化量を調べる」こと。
数学では、グラフの傾きを調べることにあたります。
例えば1次関数だと、何処でも常に同じ傾きですよね。

でも、2次関数だと場所によって傾きが異なります。

これを計算で出すのが微分です。

これが物理と何の関係があるのか？
例えば速度について考えてみましょう。

速度と言うのは、
「1秒で何m移動したか」
「1時間で何km移動したか」
みたいな量ですよね。
もう少しちゃんと言うと、
「単位時間にどれだけ座標（位置）が変化したか」
と言えます。
つまり、速度とは座標の変化量なのです。

具体例1：等速運動

例えば、人が一定の速度で歩いていると考えましょう。
横軸を時間$${t}$$、縦軸を位置（歩いた距離）$${x}$$として、グラフにしたら、下のような感じになったとします。

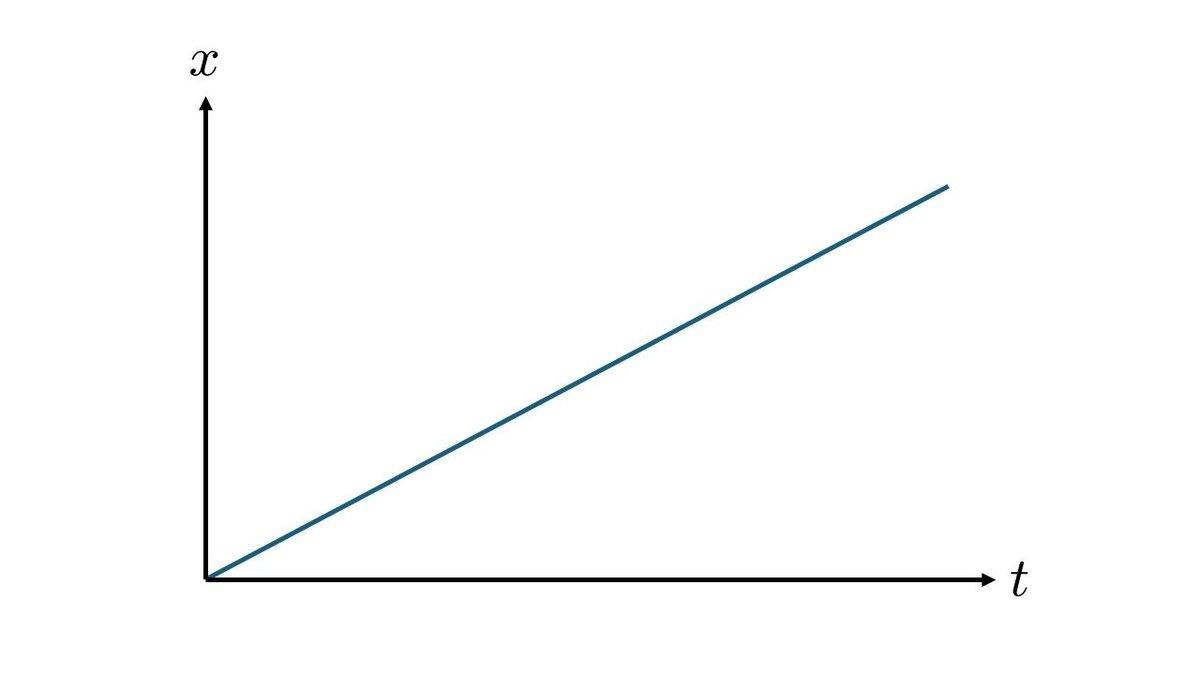
一定のペースで歩いているのが分かりますよね。
一次関数的なので$${x = at}$$と書けます（$${a}$$は適当な比例定数だと思ってください）。
一次関数なので、傾きが一定です。
傾きと言うのは、変化の割合とも言いました。
今回で言えば

$$
\def\arraystretch{5}
傾き = 変化の割合 = \frac{xの増加量}{tの増加量}
$$

ですね。つまり、時間をかけてどれだけ移動しているかということ。
これは速度に他ならないですよね。
ということで、傾きは速度を意味します。
今回の傾きは$${a}$$なので、これが速度です。
定数ですね。
速度は英語でvelocityなので、$${v}$$で表すことが多いです。
ということで、

$$
x = vt
$$

という式になるわけです。

まあ、ここまでは微分とかあんまり気にしなくて良い話です。

具体例2：加速運動

次に、車がどんどん加速するような運動を考えてみましょう。
横軸を時間$${t}$$、縦軸を位置（走った距離）$${x}$$として、グラフにしたら、下のような感じになったとします。

2次関数の形で動いているので、$${x=at^2}$$と書けますよね（$${a}$$は適当な比例定数だと思ってください）。
この場合、各瞬間でグラフの傾きが異なりますよね。

この各瞬間の傾きが、その瞬間の速度になるわけです。
この、各瞬間の傾きを算出することを「微分」というのです。

では、どうやって計算するのか？ということになるわけですが…
ちゃんとした出し方はあるのですが、今回は「物理のための」と銘打っているので、いきなり答えを紹介します。
$${x^2}$$を微分すると$${2x}$$となります。
つまり、今回はこうなります。

$$
x=at^2
$$

のとき、各瞬間$${t}$$での傾き、つまり速度$${v}$$は

$$
\def\arraystretch{3}
\begin{align}
v &= a\times 2t \nonumber \\
&=2at \nonumber
\end{align}
$$

1秒経ったら$${2a}$$ずつ増えていくという式になっています。
つまり、加速するのです。
この加速する度合い$${2a}$$を「加速度」と言います。
が、2がついているとかっこ悪いので、もともとの式を書き換えます。

$$
x=\frac{1}{2}at^2　のとき
$$

$$
v=at
$$

となります。加速度は$${a}$$ですね。
加速度は英語でaccelarationと言うので、このまま$${a}$$を使うことが多いです。

なんとなく、微分の効力が分かっていただけたでしょうか？
微分をすると、変化の割合が分かるということです。

微分の書き方、計算方法

ここまで、微分のやり方を適当に書いてきたので、少しちゃんと記しておきます。

まず今回取り上げた式をちゃんと書くと、次のようになります。

$$
\def\arraystretch{3}
\begin{align*}
v &= \frac{dx}{dt}　　\cdots (1)\\
a &= \frac{dv}{dt} 　　\cdots (2)
\end{align*}
$$

(1)式が意味するのは、「$${v}$$は$${x}$$を$${t}$$で微分したものだよ」ということ。
(2)式が意味するのは、「$${a}$$は$${v}$$を$${t}$$で微分したものだよ」ということです。

下記のように書くこともあります。

$$
\def\arraystretch{3}
\begin{align*}
v &= \frac{d}{dt}x \\
a &= \frac{d}{dt} v\\
\end{align*}
$$

これが微分の表記法です。

次が物理でよく使う微分の公式です。

$$
\def\arraystretch{3}
\begin{align*}
\frac{d}{dx} x^n &= nx^{n-1} \\
\frac{d}{d\theta} \sin{\theta} &= \cos{\theta} \\
\frac{d}{d\theta} \cos{\theta} &= -\sin{\theta} \\
\end{align*}
$$

ここに上げた最初の式が、今回使ったものです。
つまり、

$$
\def\arraystretch{3}
\begin{align*}
\frac{d}{dt} t^2 &= 2t^{(2-1)} \\
&= 2t
\end{align*}
$$

ということ。

微分の具体例

では、物理で微分を使う具体例をいくつか紹介します。

座標（変位）$${x}$$・速度$${v}$$・加速度$${a}$$については先ほど紹介した通りですが、単振動の場合は以下のようになります。

$$
\def\arraystretch{3}
\begin{align*}
x &= A \sin{\omega t} \\
v & = \frac{dx}{dt} = A \omega \cos{\omega t} \\
a &= \frac{dv}{dt} = -A \omega^2 \sin{ \omega t} \\
 &= -\omega^2 x
\end{align*}
$$

電磁気では電位$${\phi}$$を空間（座標）$${x}$$で微分すると電場$${E}$$になります。

$$
\def\arraystretch{3}
\begin{align*}
E = - \frac{d}{dx} \phi
\end{align*}
$$

点電荷の場合、以下の通り公式が導けます。

$$
\def\arraystretch{3}
\begin{align*}
\phi &= k \frac{q}{r} \\
E &= - \frac{d}{dx} \phi = -k \frac{q}{r^2}
\end{align*}
$$

では次に、積分について見ていきます。

それぞれ細かくは説明しませんが、ある物理量の変化を調べると、別の物理量になるというのが大事です。

積分とは

積分というのは、ある量が積み重なった総和を調べる方法です。
数学で言えば、グラフの下部分の面積を求めることにあたります。

例えば1次関数なら、台形の面積を求めることに等しいです。

この面積と言うのは、ざっくり見たら、細い帯をいくつも重ねたものと捉えることもできそうですよね。

この考え方が積分です。
この帯を極限まで細くして、すべてを足し合わせることなのです。

これが物理と何の関係があるのか？
今度は移動距離について考えてみましょう。

移動距離とは、千里の道も一歩からと言うように、少しずつ移動した距離の積算値ですよね。
積分の考え方そのものなわけなのですが、具体的にグラフとどう関係あるのか、見ていきます。

具体例1：等速運動

微分のときと同じく、人が一定の速度で歩いていると考えましょう。
横軸を時間$${t}$$、縦軸を速度$${v}$$としてグラフにしたら、下のようになるはずです。

等速なので、ずっと$${v}$$は変わらないわけです。
この時、例えば速度が$${v_0}$$で一定で、移動時間が$${t_0}$$だとしたら、移動した距離は、$${v_0 t_0}$$ですよね。ということは、まさに長方形の面積と一致するわけです。

これは一番分かりやすい例です。
では、次に、加速する場合を考えてみます。

具体例2：加速運動

同様に、車がどんどん加速するような運動を考えてみましょう。
横軸を時間$${t}$$、縦軸を速度$${v}$$としてグラフにしたら、下のような感じになったとします。

滑らかに加速していますが、これが段階的に加速していると仮定すれば、各瞬間は等速になります。

ということは、等速の場合の移動距離を足し合わせれば、トータルの移動距離になりますよね。
この分割を極限まで細かくすれば、結局グラフの下の部分の面積を求めることと一致するわけです。

結局、台形の面積ということになりますね。
具体的に、初速度が$${v_0}$$、加速度$${a}$$で$${t_0}$$の間だけ動いたとしたら、どうなるでしょうか？
加速度が$${a}$$ということは、$${t_0}$$経つと速度が$${at_0}$$増えているので、こういう感じになります。

ということは、台形の面積は、

$$
\def\arraystretch{3}
\begin{align*}
 & \frac{ \lbrace v_0 + (v_0+at_0) \rbrace \times t_0 }{2} \\
= & v_0 t_0+ \frac{1}{2}a t_0^2 
\end{align*}
$$

となるので、これが移動距離になります。
結局、「速度を時間で積分したら移動距離になる」ということです。

※ただし、これは実は正確ではありません。なぜなら、速度がマイナスになる場合もあるのです。はじめは右に行っていたのに、途中で左にターンしたような場合、「移動距離」という言い方では余計に計算してしまうことになります。正しくは移動距離ではなく「変位」や「座標」と言った方が良いでしょう。

積分の書き方、計算方法

ここまで、積分のやり方というようなやり方を書いてきていません。幾何学的に解けてしまいました。
ここからは、数学的な記法を記します。

今回取り上げた速度と移動距離の関係は、以下のように書けます。

$$
\int v(t) dt = x
$$

$${\int}$$はインテグラルと読み、積分することを意味する記号です。
上の例では、$${v(t)}$$を$${t}$$で積分するという意味になります。
$${v(t)}$$を$${t}$$で積分したら$${x}$$になるよ、ということです。

ここで、敢えて$${v}$$ではなく、$${v(t)}$$と書きました。
これは、$${v}$$は$${t}$$の関数であることを明示的に記しているということです。関数の形で計算方法が違うわけです。

計算方法ですが、ざっくりと、積分は微分の逆になると考えてもらえればよいです。
ですので、例えば以下のようになります。

$$
\def\arraystretch{3}
\begin{align*}
\int k dx &= k x （※kは定数）\\ 
\int x^n dx &= \frac{1}{n+1} x^{n+1} \\ 
\int \sin{\theta} d\theta&= -\cos{\theta} \\
\int \cos{\theta} d\theta&= \sin{\theta} \\
\end{align*}
$$

今回の例では以下のような感じになります。

$$
\int( v_0 + at )dt = v_0t + \frac{1}{2}at^2
$$

積分の具体例

では、物理で積分を使う具体例をいくつか紹介します。

仕事$${W}$$と力$${F}$$の関係は、

$$
W = \int F dx
$$

熱力学においては、仕事$${W}$$と圧力$${P}$$の関係は、

$$
W=\int P dV
$$

と書けます。

ここでも細かくは説明しませんが、ある物理量をどんどん足していくと、別の物理量になるという考え方が大事です。

まとめ

以上、本当にざっくりと、簡単に微積分のお話でした。
まとめると、

• 微分は変化量を計算する手法

• 積分は積算値を計算する手法

• 計算方法よりも考え方が大事

といったところ。物理量同士の関係（$${v}$$の時間変化が$${a}$$になる、など）を意識することで、公式を覚えなくても導くことができたりするので、身につけたら強い武器になります！
大学以降では絶対必要になってくる考え方なので、目指している方は是非今のうちに慣れておくといいと思います。