
金融庁がスケープゴートにした一時払外貨建て保険と外国債券投資の関係と為替リスクの矛盾(総集編2024)
本記事では債券投資と一時払外貨て建保険の仕組みについて解説していきます。
5月中旬に公開予定の「一時払外貨建て保険に対する販売規制と金融庁の示す販売指針への不信感」と併せてご覧ください。
一時払外貨建て保険は債券投資を保険会社という間接金融の仕組みを用いることで商品化しています。つまり債券投資について理解することがそのまま、一時払保険について理解することになります。
ここ最近、金融庁がメディアを通じて一時払外貨建て保険についての苦情が増えている上に早期解約が目立つと報じてまるで良くない商品のような印象操作がされていますが、客観的に考えてそれは大きな誤解であることを説くのがこの記事の目的です。

債券と一時払外貨建て保険については過去に散々、何度も書いていますのでこの辺り(有料記事含む)もご参考にしていただければと思います。
今回はこれらをまとめた総集編(2024)です。
債券投資
債券金利と債券価格の関係
株式は投資した原資をいつ換金するかの期限が予め定まっていないため価格(時価)で売買されますが、債券は満期が予め定まっているため金利で売買されます。
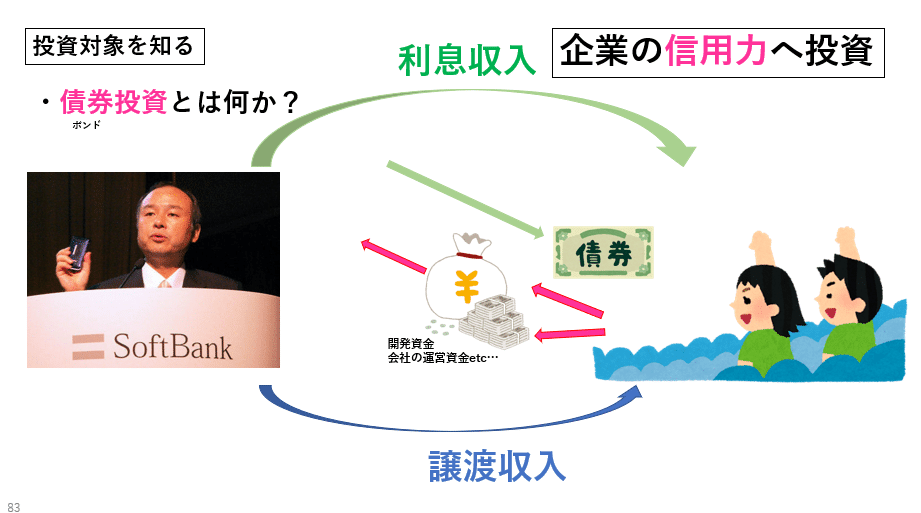
債券は株式と同様に企業が資金調達をするための手段の一つですが、株式と異なる点も多い金融商品です。
その最たる点の一つが、その企業が債務不履行を含む破綻をしなければ満期時に元本が戻って来るという点です。
金利と国債・社債の相互関係

その国(政府・財務省)の発行する債券「国債」は、その国で事業を行う全ての企業のリスクの基準となります。
何故ならその国で事業を行うとはその国の発行する通貨建で売上が上がり、家賃や賃金を支払い、納税を行うからです。
国債につく金利を「市場金利」またはパッシブリスク(リターン)と呼び、その市場金利に企業固有の財務・破綻リスクに応じたリスクプレミアムが上乗せされた金利がその企業の発行する債券金利となります。
債券金利は満期までの期間が長いほど一般的にはお金を貸している側が返してもらえないリスクに加え、物価上昇によって貸した元本が戻ってきてもお金の価値が減っていることを防ぐために長期になるほど金利が高いことが一般的です。

少し専門的には、長期ほど金利が高くなる現象(右肩上がり)を順イールドと呼び、それが垂直に近づくことをスティーブ、逆に右肩下がりになることを逆イールドと呼んでいます。
金利が高いことは投資家としては嬉しいことばかりではなく、貸し倒れリスクが高い対象であるほどに金利が高いことの反映でもあります。

借金の返済期限が来てものらりくらり、または踏み倒してばかりの人にお金を貸そうと思う人はいません。金利にはそうした貸し倒れリスクを考慮した金利が需要と供給に対して合致したところで付けられます。

各国の中央銀行は通貨発行権を独占的に有すると共に、金融政策を決定する権利も政府から独立して持っています。
(実際にはその国の財務省の意向が反映されるが)
中央銀行は1年以内の金利を決定します。
これを決める会合を金融政策決定会合と呼びます。

米連邦公開市場委員会(FOMC)で決定・発表される。
そして1年超の金利は市場が需給によって決定するのが一般的です。

政策金利を上げたり下げたりする事で市中に流れるお金の供給量を増やしたり、減らしたり…

こうして経済が活性化するように、またはあまりに消費が拡大しすぎる物価高の場合にはそれを抑制しようとする効果に働きかけます。
こうして「通貨価値の安定」を計ることが中央銀行の最大の使命であり、中央銀行による金利の上げ下げなどの金融政策や通貨発行などはそのための手段にすぎません。
債券価格と金利の関係
国が国債を発行するように、地方自治体は地方債、会社は社債を発行します。これらを合わせて公社債と呼ぶこともあります。

元本100万円の満期(償還日)まで1年とした債券があったとします。
債券には金利がもらえる利付き債、金利の代わりに価格が最初から割り引かれている割引債などがあります。

割引債を例に考えると、金利1%の債券の満期1年前時点での債券価格は99万円となり、1年後に100万円の元金が戻ってきます。
満期の100万円からみて1%増えたことになるため、1%の金利を受け取ったのと同じ資産運用の効果があったことになります。

仮に同じ発行体が発行する債券が満期まで1年、金利が3%の債券だった場合、1年前の時点で債券価格は97万円になります。
満期まで1年の時点で金利1%と3%の時では99万円と97万円の差ということで、金利が高くなると債券価格は2万円安く手に入れられることになります。

言い換えると購入した時に金利3%だった債券が、金利1%に金利が下がった状態では債券価格97万円が99万円になるため、利下げは債券価格の上昇となります。
こうした金利と価格の関係が逆に動く債券特有の現象を保険業界では「市場価格調整(MVA)」と呼んでいます。(平準払はこの機能を原則採用していない)

そしてMVAは外貨建て保険のリスク説明の一つとして為替リスク・価格変動リスク・金利変動リスク、解約控除や諸経費が差し引かれている事と一緒に必ずパンフレットや設計書、契約概要・重要事項説明書等で説明することと、これまでの投資経験やこうした金融商品特有のリスクについての理解をしているかの適合性確認が義務化されており、かつ意向確認と同時にこうしたリスクについて理解しているかを契約者に念押しして確認を取っています。
ここにレ点と日付・署名をした時点で契約者にとって知らなかったは弱者の言い訳として基本的には扱われる。
但し、日本は建前上は弱者にやさしいので消費者相談センターおよび保険会社・保険代理店、金融ADR、金融庁にそのクレームは逐一報告される。類似のケースが多い*と販売している現場でおかしな提案の仕方をしていると行政が考えて動く仕組み。
*なお、クレーム発生率ではなく件数で見ているので今回のようなことになる。一時払外貨建て保険の販売が世の中で増えれば、クレームの件数が増えてみえるのも当たり前の話、但し無視して良いとはならない。

尚、当たり前ですが債券は満期に近づくほど、債券の価格変動は小さくなることも念頭に置いておく必要があります。
1年満期や5年満期、または国債*などのように10年、20年、30年など期間が長くなれば金利は同じ3%だとしても債券価格の変動(変動する金額)は変わってきます。
*破綻リスク増大や経営者交代、買収など財務状況がそこまで長期で見通せないため一般的に国債・地方債以外は10年を超える債券を発行しない。
元金100万円で1年(3%=3万円)、5年(3%=15万円)、10年(3%=30万円)、20年(3%=60万円)、30年(3%=90万円)…①
これらがもし1%まで金利を下げれば1年(1%=1万円)、5年(1%=5万円)、10年(1%=10万円)、20年(1%=20万円)、30年(1%=30万円)…②
金利が高い時に買って、金利が下がった時に売れば①-②の差額が儲かる計算になります。
逆に金利が低い時に買って、金利が上がってから売ると②-①の差額損をするため、途中売却をする可能性がある場合には金利が低い債券は買ってはいけないとなります。
たとえば日本の場合、政策金利がマイナスまたはゼロ金利より低い状態は通常あり得ない状態です。

これを更に▲1.0~▲2.0%としていくことは現実的にほぼ考えづらく、0.00%や0.25%、1.0%と段階的に利上げしていくことが想定される状況において円建て債券(一時払保険)をわざわざ買うという選択肢は個人投資家には"全くない"と言えます。
契約当初は途中売却をする予定があろうとなかろうと、5年10年という中長期的には急にお金が必要になるケースというのはよほどの資産家や富裕層でもない限り誰にでも起こりえる問題です。
特に外貨建ての場合には為替の変動によって円安が進み、契約当初に想定していた利益が早めに確保できる場合もあれば、円高が進み当初よりも期間を延長して運用を続けた方が良い場合など様々です。
金融商品に限らず言えることですが、人生というのはなんでも自分の思い通りにいくようなものではありません。
思い通りにいくのは多くの場合、空想の世界などです。

人生は理不尽であることをまず受け入れなければ、人はいつまでも学生気分または子ども時代の思考から抜け出せず自分以外の誰かのせいにして責任を取らずのうのうと生き続けることになります。
利上げが見込まれる場合、円建て一時払保険は検討の余地がないとして資産運用を考える場合には、金利が高く世界中の貿易を含む決済で基軸通貨となっている米ドルなどの外貨建てがその対象となります。
米ドルなどの外貨資産を保有することは、単に資産を増やすだけでなく資産を守る意味もあります。仮に100万円の日本円を資産運用を米ドル建てで行った場合、金利がついて増えた部分はドルから円に戻す際の円高ダメージの相殺・軽減にもなります。
ユーロ建ては取扱保険会社が少ないだけでなく、個人的に欧州は色々な理由で大変厳しいだと思っているのでお勧めしない。
豪ドルはまぁ米ドルに資産が偏っていると思うなら一部分散しても良いと思うが、積極的に投資するかどうかは意見が分かれるところ。
一時払と平準払の運用効率の違い
多くの日本人にとって保険契約とは一時払ではなく月払や年払など少しずつ保険料を支払っていく平準払と呼ばれるものの印象が強いかもしれません。
平準払は同じ"資産性保険*"の中でも保障性にやや重きを置いているプランです。
*お金が貯まったり運用される保険。対義語は保障性保険(掛け捨て)
平準払は少額から保障を持てるという点で人気が高い一方で、保険関係費の一部である事務コストが発生します。

平準払は口座振替またはクレジットカード払などの収納コストが数%(約0.5~3.5%)にも及びます。
収納手数料は契約者の保険料から都度差し引かれるため資産性保険の場合、運用効率が必ずしも良いとは言えません。
一時払の場合、契約時に振り込む保険料のみのためこうしたコストがかからず保険締結費用や保険関係費などの最低限のコスト差し引かれ、残ったお金が運用に回ります。
保険における資産形成プランとは、いわば保険料に諸経費コミコミで手続きをする事ができるパッケージプランと言えます。
そして保険会社は金融庁に届出をして認可を受け、集まった資金を利用して債券を購入し、保険金支払い事由を設定し、様々なタイプの一時払保険販売します。

このため債券の金利や価格変動と殆ど類似の仕組みの金融商品となり、債券を応用させた"高度な金融商品"となります。

この高度…つまり理解をするための知識・投資経験などを補い、顧客を保護するものが間接金融の仕組みであり、保険募集人(担当者)や保険会社の担っている役割となります。
さて平準払と一時払でどれくらいの違いがあるのでしょうか?
ここから先は
この記事が気に入ったらサポートをしてみませんか?

