
問題タイトル「Triangle Utilization」の解説
2022年11月13日にPuzzle Square JPに投稿した問題、「Triangle Utilization」の解説を行います。
問題はこちらから遊べます。


右下の「→1」は単純仮定で確定できます

赤枠で囲った列を見ると、線が3本通過しているので、偶奇より「↓4」の上のマスには線が通ることが分かります。

辺の手筋より黄色マスには黒マスを最大1個しか入れられないので、オレンジマスは黒マスで確定します。

中央付近の「←2」の右のマスは単純仮定で確定

赤枠で囲った空間の偶奇を考えると、すでに線が2本入っているので×のところは線が通りません。

この先は先読みで攻略することも可能です(おそらくそれが一番楽)。先読みする場合は「↑1」の真上のマスが黒マスかどうかで考えるとスムーズです。
しかし、ここはあえて理詰めで攻略してみましょう。

ヤジリンには、「隅にあり内部にヒントのない上図のような6マスには黒マスを1つまでしか置けない」という性質があります。

まず、出口の手筋より青マスには黒マスを置けません。
残りの4マスについて、それぞれ黒マスが入ると線がどのような挙動を取るか見てみると……

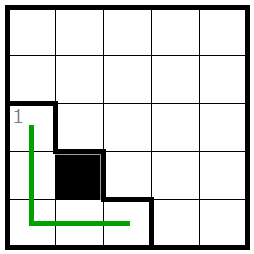


このように、どこか1マスでも黒マスが入ると他のマスすべてに線が引かれてしまう形になるため、2つ目の黒マスを置くことができないのです。
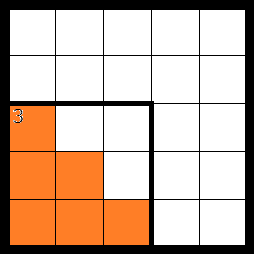
本問では使いませんが、上記の性質を使うと、「隅にある内部にヒントのない3×3の領域に黒マスを3個入れられるパターンは1通りしかない」ことを簡単に説明できます。
オレンジマスには黒マスを1個しか置けないため、残りの3マスに黒マスを2個置く必要がありますが、そのような置き方は1つしかありませんね。
問題に戻ります。

オレンジマスには黒マスを1個までしか置けませんが、ピンクのヒントを見ると横方向に1個、縦方向に1個の黒マスが必要なようです。

ということは、交点に置くほかありません。

最後は地味に偶奇!!!!!!で、あとは埋めれば答えとなります。

本問の解説は以上です。
ここまでお読みいただきありがとうございました!
この記事が気に入ったらサポートをしてみませんか?
