第１４話　法律家のたしなみ　前編

「素因数分解？」
　陽菜はるなが小首をかしげた。
「おう。ネットで調べてみたらな、素因数分解ってめっちゃ難しいらしい。たとえば素数$${2}$$つのかけ算は割と簡単にできんねんけど、逆にそれを分解しようとすると、数字のデカさによってはコンピューターでもごっつい時間かかるんやと。」
「まあ確かに、見た感じすごくメンドくさそうではあるけど・・・。」
　陽菜は、大翔ひろとが持って来た絵馬算額をしげしげと眺めた。

次の数を素因数分解せよ
$${432652837}$$

　日曜日の昼過ぎ。塵劫じんこう神社の境内。
　当初はあまりここへ来たがらなかった大翔だが、なんだかんだで今日も来てしまった。もちろん算額の返事を出すためというのもあったが、昨日から個人的な数学ブームが再来していた。塵劫神社ここでもう少しねばれば、ワンチャン数学の点数が上がるかもしれない。

「大翔はこれ、分解できるん？」
「無理。やったけど挫折ざせつした。」
　$${1}$$ケタの素数でわり切れないのは簡単に確認できた。$${11}$$の場合も、先週知った公式を使うと手計算で行けた。
「$${13}$$以上はさすがに電卓使つこたけど、上・に行くほど、そもそもなにでわればええんか、だんだんわからんなってくんねん。」
　$${19}$$ぐらいまでなら、少し考えればなんとか素数かどうか思い出せる。だが$${20}$$を超えたあたりから、だんだん数字がゲシュタルト崩壊し始めた。$${21}$$を一瞬素数だとカン違いし、$${27}$$にいたって、とうとうわり算までやってしまった。
「え、ひょっとして、また答えわからへんやつ？」
「いや、答えだけはわかっとるで。むしろ、答えの素数を先にネットで調べてから、電卓でかけ算したんがそれ・・や。」
「えええ・・・。それ、ええのん・・・？　自分では解けへん、て。」
　陽菜があきれた顔をすると、横で聞いていた吉栄光比売よしざかえひかるのひめが口を挟んできた。
「普通はあかんと思うが・・・。まあ、ええんとちゃうか？　答えが存在せん問題を出してるワケやないし。」
「ほれほれ、先生も『ええ』言うてるやんけ。」
　大翔が陽菜に向かってドヤ顔をする。
「第一、今までのやり取りで、向こうも俺らも解き方なんていちいち書かへんかったやろ。今さらええやんけ。」
「けどぉ・・・。」
「つうか、俺は俺で他に素因数分解の宿題があんねん。数学徒 X・・・・がその問題に手こずっとる間に、そっちやってまわなあかん。」
「？」
「昨日言うてた、RSA暗号の話かえ？」
「そうっす！　あれ、素因数分解したら答えわかるんでしょう？」
　昨日、叔父の豪ごうから出されていた暗号解読の宿題。彼曰く、RSA暗号は公開鍵が素因数分解できてしまうと、解読に必要な情報がすぐにわかってしまうという。逆にそれができないと、解読は非常に困難だとか。
　どのみち素因数分解をしなければいけないなら、答えが分かりきっている自分の問題ではなく、叔父からの宿題の方を優先するべきだろう。もっとも素因数分解できたところで、その結果をどう使えば暗号が解けるのかはまだわからないのだが・・・。
「つーわけで、俺は暗号の方をやる。お前は試しに、俺が作ったその問題解いてみいや。」
　そう言ってから、大翔は後悔した。いい感じの難問を作れたことに浮かれ、うっかりその勢いで幼馴染を挑発してしまった。「さすがに怒られるか？」と思ったが、彼女の返答は意外なものだった。
「んー。わかった、やってみる。」
「ほ？　やるんか？　結構ムズいぞ？」
「ええよ。おおよその見当はつくから。」
「へ？」
「ほう？」
　彼女のあっさりとした返しに、大翔と吉栄光比売は同時に反応した。
「たぶんやけど、だいたい同じぐらいの大きさの素数$${2}$$つと違うん？」
「何でわかんねん？！」
「だってぇ・・・。大翔、いじわるやもん。少しでも問題が難しくなるようにしてるやろ、絶対。素因数分解って、小さい数から順にわり算していくやん？　せやし、すぐに正解がわからんように、めっちゃ大きい素数持って来たんちゃうん？　で、素因数をたくさんようさん見つけてくるのも、それをかけ算するのもメンドくさいから、素因数はだいたい同じ大きさの$${2}$$つ。」
　これを聞いて、大翔は思わず白目をむいた。吉栄光比売はとなりで大笑いしている。どんなするどい数学的な考察が来るのかと思ったら・・・。
「メタ読みすんなや・・・。」
「ええやん。立派な推理やって。」
「推理するのはええけど、どうやってやる気や？」
　吉栄光比売が興味深げにたずねた。
「んーと。ヨシザカエ様、またケサランパサランこの子ぉら借りてもええですか？」
「ああ、ええよ。432652837匹、耳そろえて持っていき。」
「ありがとうございます！　こっち来てー。」
　陽菜が境内の真ん中あたりに向かって歩き出すと、どこに隠れていたのか、境内を覆い尽くさんばかりの数のケサランパサラン達が現れ、彼女について行った。その様子を見ながら、大翔がつぶやいた。
「ここ数日で、急激に魔女っぽくなって来ましたね、あいつ。」
「？　そうかえ？」
「俺はそのうち、あいつの合図でヤツらが竜巻みたいに空に舞い上がるようになるんちゃうか、思おもてます。」
「そこまで行ったら、もう神やなぁ。」
　漫画やアニメなら、世の無情をなげいた少女がケサランパサランの大群を引き連れて、世界に復讐を始めるというストーリーもありそうだ。陽菜に限ってはその心配はなさそうだが。

「！」
「？」
　ふと、吉栄光比売が眉をひそめ、拝殿の裏側の方・・・・を振り返った。大翔も同じ方向を振り返ってみたが、彼にはなにも見えない。
「ちっ・・・。めんどくさいのが来よったわ・・・。」
　女神は頭をかくと、そちらの方へ向かって「ススス」と移動して行った。
「何すか？？　誰か来きはったんですか？」
「お主は来こんでええ。」
　振り返りざまに、吉栄光比売がピシャリと制止してきた。硬直した大翔を残し、彼女は拝殿の裏側へ消えてしまった。
　すると数秒して、野太い男の声と、それに応える吉栄光比売の声が聞こえて来た。内容は聞き取れないが、吉栄光比売がイラついていることだけは声のトーンから読み取れた。
「なんや、なんや？　先生の男友達・・・か？」
　興味に駆られてそちらへ行こうと足を踏み出したものの、さきほどの彼女の言葉を思い出し、思いとどまった。これでまた円周率を詠唱させられたら、たまったものではない。

　大翔は絵馬３枚を取り上げると、絵馬殿の前に立った。後ろでは、陽菜がケサランパサランに号令を出している。彼は絵馬をかけながら彼女に聞いた。
「お前そういや、今朝、なんか変な夢見ィひんかったか？」
「夢？」
　彼は今朝、野生動物に重傷を負わされる夢を見た。おそらくは、先日の幻覚と同じ人物・・・。
「んー。今朝の夢は、アテナ製菓のハムスターフルーツ大福と四辻屋のカステラとモチダ珈琲店のパフェと・・・。」
「ん、平和な夢を見たようで何よりや。」
　どうやら陽菜は今回、幻覚を見なかったようだ。
　それでよかったような気がする。今回のあの幻覚（夢？）は、さすがに刺激が強すぎる。温厚な陽菜が見たら、どんなショックを受けるかわからない。
　前回この神社で幻覚を見たのは、算額を奉納した直後だった。なので幻覚と算額には何らかの関係があると見てよさそうだが、今日は絵馬殿に算額を奉納して数分たっても、先日のように幻覚が現れる様子はない。やはり、今朝見た夢が今回分の幻覚なのだろう。そして、陽菜が幻覚を見ていないということは・・・。

「んんんー。　ちゅうか、ぜんぜん進まへん・・・。」
　大翔が考え事をしていると、後ろで陽菜がぼやいた。
「どないしてん？」
「たぶん、このやり方で行けるはずやとは思うんやけど・・・。」
　彼女の目の前には、ケサランパサラン達がほぼ・・長方形の形に並んでいた。
「最初、できるだけ大きい正方形作るところから始めてん。で、そこからすこしずつ移動させて、長方形の形にしようとしたんやけど・・・。」

ほぼ正方形から長方形へ

「待て待て。いったん待て。」
　大翔は陽菜を制止して、彼女の説明に出て来た数字を電卓に打ち込んでみた。

$${20800^2+12837=432652837}$$

「お、おお・・・。ちゃんと合おうてるな。お前、ようこんなデカい数、１コも間違わずに数えられるな。」
「そこはまあ・・・なんとなく。『えいっ』と・・・。」
　魔女、ここに極まれり、である。
「まあそれはともかく。ちゃんと長方形になったら、あとは辺の長さ調べるだけでええやん？　そやけど、やってもやってもぜんぜん長方形にならへんのよ。」
「・・・・・・。」
　大翔はしばらく考えていたが、突然パンと両手を合わせた。
「そらお前、このやり方やったら時間ヒマかかって当然やろ。」
「なんで？」
　さすがの魔女も、数学は手に余るようだ。
「このやり方って、要するに縦の数で何回もわり算やってるようなもんやん？」

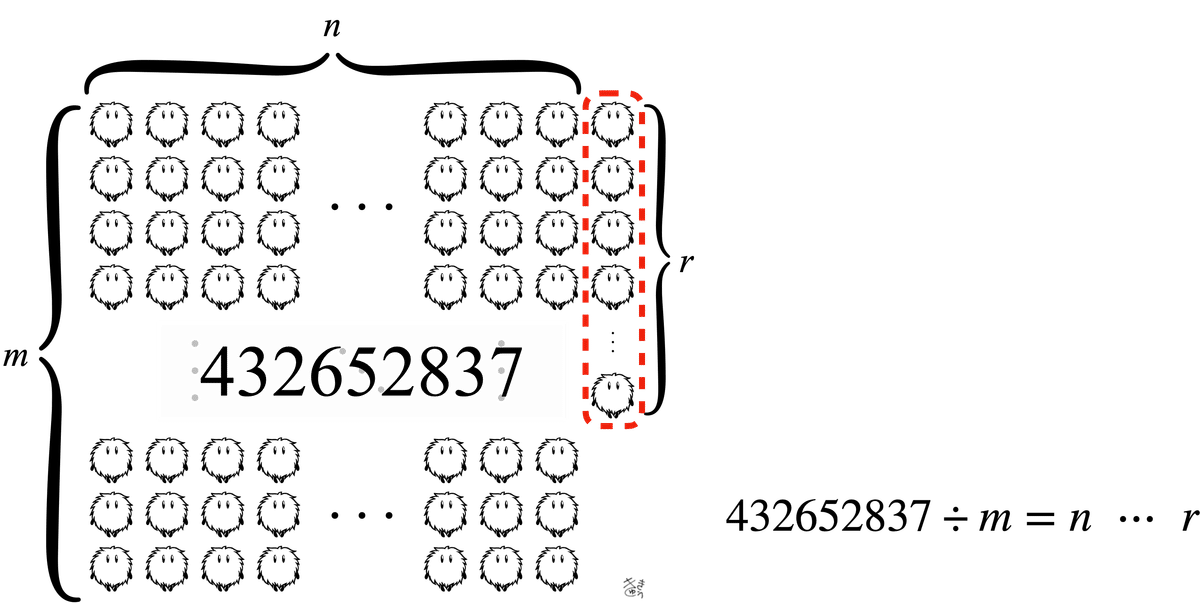
「そやけど？」
「それを$${1}$$行ずつ減らして行ってたら、そら時間かかるって。せめて$${2}$$行ずつ、奇数でやらんと。」
「なんで奇数ってわかるん？」
「ええっとやな・・・。」
　そこで大翔はカバンから数学の教科書を取り出し、該当のページを見つけて陽菜に示した。
「ほら、やっぱり。かけ算の結果が奇数になるのって、奇数同士をかけた場合だけやねん。$${432652837}$$は奇数やから、縦の数が偶数のときはぜったい長方形にならへんって。」
「あ、そっか・・・。」
「せやけど、$${2}$$行ずつ減らしたとしてもメンドくさいな・・・。」

「あんた達あんたやら、解けたんかえ？」
　２人で頭を抱えていると、吉栄光比売が話しかけて来た。
「あ、先生！　お客さんは帰りはったんですか？」
「お客さん？」
「おお。なんかさっき誰か来はったみたいで、先生出迎えてはってん。どうも、男の人っぽかったけど・・・。」
「え？！　ひょっとして、ヨシザカエ様の彼氏・・・じゃないみたいですね・・・。」
　“彼氏”と聞くやいなやの鬼の形相ぎょうそうに、２人は縮こまった。日本の神様には、元は鬼だったというケースもあるらしいが、ひょっとしたら彼女もそうなのかもしれない。
　どういう客人が来たのかはわからないが、何にせよ、触らぬ神に祟りなしである。大翔は、客人の話はなかったことにして、陽菜の解き方について説明した。
「はあ、それは時間かかるわな。いつかは解けるやろけど。」
「ええ・・・。」
　陽菜がガックリと肩を落とす。ケサランパサランをあやつっていたときの強者感はどこへやら。
「ほなまぁ、試しに最後までやってみるかえ？　その解き方で。」
　吉栄光比売が手をかざすと、ケサランパサラン達があっという間に正方形っぽい形にならび、そこからすさまじい勢いでならびかえが始まった。動画の倍速再生などというレベルではない。もはや、連中は瞬間移動している。これがホンモノの神か。
　１分かそこらで、ケサランパサランがキレイに長方形にならんだ。陽菜が縦横の数を数える。
「$${21701\times19937}$$・・・か。合うてる？」
「合うてる、合うてる。」
　大翔がスマホに保存していたメモと、完全に一致している。めでたく問題は解けたわけだが、あまり感動はない。
「なんか・・・。平方根ぐらいからスタートしたら、早はよ終わるかと思いましたけど、結構時間かかるもんすね。」
「そりゃそら、$${2}$$から順番にやるよりかはぜったい早いえ？　せやけど、いかんせん、元の数が大きすぎるわ。$${2}$$行ずつならべかえて行ったとしても、$${432}$$回の操作がいるねん。$${1}$$回の操作が５秒ですんだとしても、４０分近くかかるえ。」
「そらぁ、エゲツないっすね。・・・イタッ。」
　陽菜が大翔を肘でつついた。
「ええっと・・・。すんません、このやり方、もうちょい速くやる方法とかってないんすか？」
「んん？　速いかどうかはときと場合によるから一概に言えんが、似たような方法はあるよ。“フェルマーのアルゴリズム”、いうのがあってな。」

To Be Continued…