
第11話 くり返すあまり
「そうや、思い出した! あまりはくり返すねん!」
「うん? どういうこと?」
「見てみぃ!」
大翔はあらためて、数日前のメモを陽菜に示した。
「この前話したやろ。$${10}$$のナントカ乗を$${7}$$でわったあまりって、$${6}$$乗するごとに1周するねん。」

「てことは、やで? $${\textbf{2}}$$のナントカ乗も一緒ちゃうんか? $${2^{12}}$$を$${13}$$でわったあまりが$${1}$$やったら、$${\textbf{12}}$$乗するごとに1周してあまり$${\textbf{1}}$$になるんとちゃうんか!?」
$$
\begin{equation*}
\begin{split}
2^{12}\div13&=\ ?\ \cdots\ 1 \\
\left(2^{12}\right)^2\div13&=\ ?\ \cdots\ 1 \ \text{(?)}\\
\left(2^{12}\right)^3\div13&=\ ?\ \cdots\ 1 \ \text{(?)}\\
&\cdots
\end{split}
\end{equation*}
$$
本日、二度目の大見得である。だが、今回はさきほどと違い、誰かの受け売りではない。
だが、幼馴染の反応はにぶい。
「それ、ホンマ? ホンマにホンマ?」
「いや、行けるやろ! 絶対そうなるって!」
「命かける?」
「いやまた、おおげさ・・・。」
そう言いかけて、大翔は息をのんだ。心なしか、背後にいる吉栄光比売から殺気を感じる。
いや、気のせいだ。自分にそんな第六感はないはずだ・・・。
ふと、彼のヒザをケサランパサランが1匹、よじ登って来た。つぶらな瞳で彼を見上げると、やおら身をふるわせ、モインッと2匹に分裂した。
「ひいいいいいい!」
これでまた大波に押し流されでもしたら、本当に命が吹き飛びかねない。彼は必死に思案した。
だが、命の危機にひんした彼の思考は、普段のパフォーマンスを大幅に超えた。
「さっきの定理からすると、『$${2^{12}}$$を$${13}$$でわったあまりは$${1}$$』なんやろ? それって、ようはこういうことちゃうんか?」
彼はルーズリーフにシャーペンを走らせた。
$${2^{12}=13n+1}$$
陽菜はその数式を、キョトンとした顔でながめた。
「この$${n}$$って何?」
「$${2^{12}}$$を$${13}$$でわった答えや、あまりと違て。」
「??? どういう数式、これ?」
「お前がケサランパサランの群れでわり算やってたんと同じことしてんねん。第$${1}$$項が、お前の言う$${13}$$でくくったセット、第$${2}$$項が文字通りあまりや。」
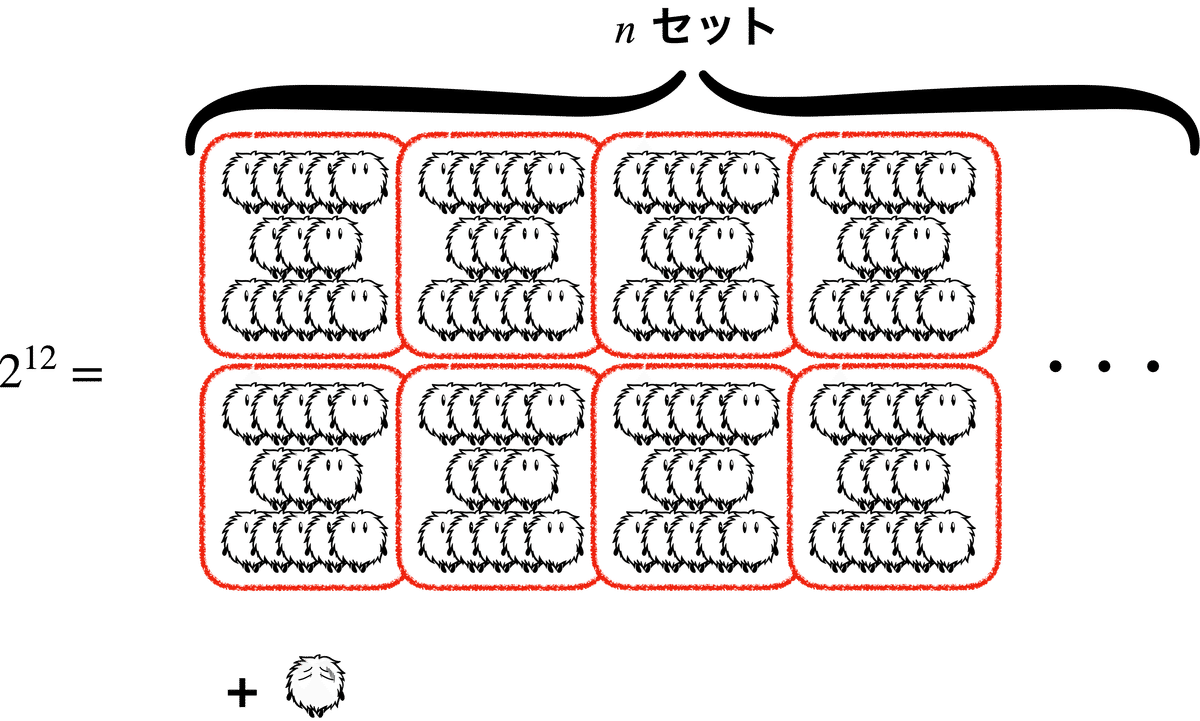
「$${13}$$匹のセットの絵を、$${``13"}$$って省略して書いてる、ぐらいに思てくれたらええ。」
「・・・ああ! おお!」
どうやら、式の内容が伝わったようである。
「ほんで、たとえばこれを$${2}$$乗するとやな・・・。」
彼はルーズリーフに$${\left(2^{12}\right)^2=\left(13n+1\right)^2}$$と書きつけた。とたん、幼馴染の目がキュッとバツになった。
「へ? いやいや、$${2}$$乗するんやから、こうなるやろ?」
キュッ。
「だから、$${(a+b)^2}$$の公式使えば・・・。」
キュッ。
「ええええ・・・。」
陽菜が数式に弱いのはうすうす気づいていたが、ここまで苦手だとは思わなかった。たしかにこれでは、テストでまともな点数は取れまい。
だが、計らずしてゾーンに入った大翔の頭の中では、かつてないほどに数式が乱れ飛んでいた。しかも、あと一息でそれがまとまりそうな予感がしていたのだ。歯車が噛み合いそうな感じ。
正直、今このタイミングでケサランパサランの群れの絵は描きたくない。
「ん〜。ほな、これならどうや?」
さんざん悩んだすえ、彼はさきほどの式を消し、代わりに別の式を書いた。

「あ! うん、これならわかる!」
「ふーう。世話焼けるやっちゃ。」
言うなれば、数式と絵の合いの子である。ずいぶんと原始的な体裁になってしまったが、これで納得してもらえるならヨシとしよう。
「ほんで、ここから$${13}$$のセットを取りのぞいていくとやな・・・。」

「な? $${2^{12}}$$の$${2}$$乗を$${13}$$でわったあまりは$${1}$$やねん。」
「・・・・・・。うん。・・・なるほど。」
長考のすえ、陽菜がうなずく。よし、順調だ。
「次に$${3}$$乗や。さっきの要領で考えると・・・。」

「うん・・・、うん・・・。わかる。」
「オーケー。で、これがこうなるんはわかるか?」
大翔は、今書いたばかりの式を少し修正した。

「わからん。どこから出て来たん、その式?」
「さっき見たやろ、$${\left(2^{12}\right)^2}$$を$${13}$$でわったあまりは$${1}$$やて。てことは、$${\left(2^{12}\right)^2}$$も$${13}$$のセット プラス $${1}$$匹で書ける、言うことや。」
「$${m}$$って何?」
「$${\left(2^{12}\right)^2}$$を$${13}$$でわった答えの方や。具体的な値は知らんけどな。」
「・・・数学ってそれが気色悪いんよ、いつも思うんやけど。なんで、答えがわかりもしてへんモンを文字に書いただけでわかった気になるのん?」
「別に、“わかった気”にはなってへんて。そもそもわかる必要もないねん。」
「えええ???」
2人の会話を、吉栄光比売は興味深げに見つめていた。
これまで彼女は、陽菜には才能を感じていたものの、大翔の方には特に光るものを感じていなかった。だが今の一連の説明を聞いている限り、彼は問題の解答にほぼ到達しているように思えた。
「これは案外、イケるクチかも知れへんなぁ・・・。」
女神は、2人には聞こえない程度の小さな声で、ニヤリと笑った。
「ちゅうか、お前さっき、$${2^{12}=13n+1}$$は納得してたやんけ。なんでそれはよくて、これはアカンねん?」
「・・・1コだけやったら我慢できるねん。『ひょっとしたら、もう少ししたら答えがわかるかも知れへん』て。せやけど、$${n}$$がわからへんまま、$${m}$$が出て来たやん。いつになったらわかるのん?」
「せやから、わかる必要はないねん。実際、$${n}$$がわからへんでも、$${\left(2^{12}\right)^2}$$を$${13}$$でわったあまりは$${1}$$やてわかったやろ? あまり知りたいだけやったら、$${n}$$は知らんでもええねん。」
「・・・・・・。$${m}$$も?」
「$${m}$$もいらん。見とりゃわかるわ。ここまで来たら、あとぜんぶ一緒やねん。」

「変わったんは、行の数だけや。それも、$${13}$$の倍数 プラス $${1}$$ってわかっとるから、結局あまりが$${1}$$になることだけは確定や。」
「・・・・・・。」
陽菜は押し黙っている。納得しているのか、していないのか。
「今の証明とほとんど同じようなこと、2、3日前にお前がやっててんぞ? 覚えてへんか?」
「?」
「『$${10}$$の偶数乗を$${11}$$でわったあまりは$${1}$$』を証明したときや。あのときは、絵描いて証明しとったけど。」
大翔は数日前の別のメモを取り出した。

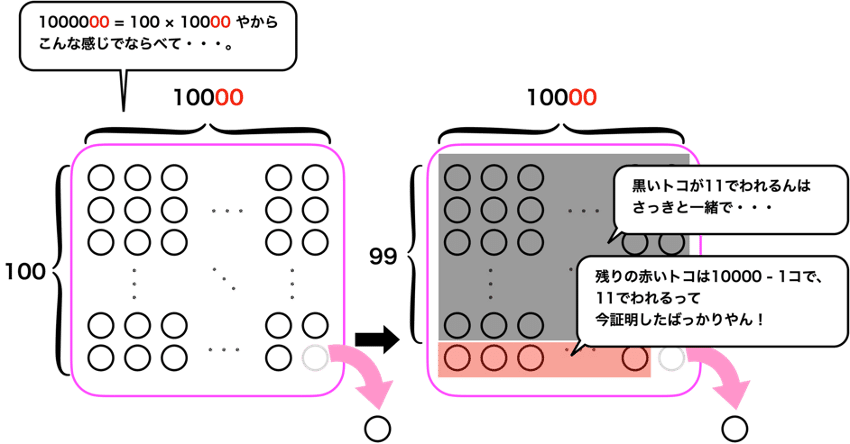
「これと考え方はほとんど一緒やで。数式で書いてるのか○で描いてるのかの違いはあるけどな。」
「ああ〜! なるほど!」
ようやく、陽菜が納得した表情を見せた。やはりこの少女、数式が壊滅的に苦手な一方で、絵にさえ描けば、一気に理解力が上がるようだ。
「で、『あとは同じことのくり返しやから』て、証明終了したんやった!」
「せやな。数学的帰納法や。俺が書いた数式でも一緒や。次の$${\left(2^{12}\right)^4}$$考えても、ほとんど同じヤツが出てきよるわ。」

「出てくる数式の形が一緒やから、結論もぜんぶ一緒や。よって・・・。」
$${2^{12}}$$のナントカ乗を$${13}$$でわったあまりは$${1}$$
大翔が結論をルーズリーフに大きく書いた。
ようやく、幼馴染に一矢報いることができた。もちろん、彼女にしてやられたのはほんの数日前なのだが、その間に彼が感じていた敗北感は半端なものではなかった。それこそ、ぬかるんでもいない地面が沼に感じられるほどの。
「ふむ。雑ではあるが、数学的帰納法使えたやないか。感心、感心。」
吉栄光比売が、珍しく、大翔を手放しでほめた。それを聞いて、大翔がガッツポーズをして見せる。
「ほんで? そのあとはどうすんねん? それが結論と違うやろ?」
「もちろんっすよ! ここまで来たら、もう解けたも同然っす!」
彼は紙を取り替えると、いさんで数式を書きはじめた。途中、ひっ算も交えつつ。
$$
\begin{equation*}
\begin{split}
2^{2024}&=2^{12\cdot168+8} \\
&=\left(2^{12}\right)^{168}\cdot2^8
\end{split}
\end{equation*}
$$
「さっき、『$${2^{12}}$$のナントカ乗を$${13}$$でわったあまりは$${1}$$』てわかったから、$${\left(2^{12}\right)^{168}}$$を$${13}$$でわったら、やっぱあまり$${1}$$っす。つまり、$${\left(2^{12}\right)^{168}=13N+1}$$って書けると。」
「その$${N}$$は、そのわり算の答え?」
横からのぞき込んだ陽菜が聞いた。
「そ! これをさっきの式に入れてやると・・・。」
$$
\begin{equation*}
\begin{split}
2^{2024}&=2^{12\cdot168+8} \\
&=\left(2^{12}\right)^{168}\cdot2^8 \\
&=\left(13N+1\right)\cdot2^8 \\
&=13N\cdot2^8+2^8\ \ \ \text{(分配法則を使った。)}
\end{split}
\end{equation*}
$$
「第$${1}$$項は$${13}$$でわれるから、あまりには関係なし! で、$${2^8}$$は・・・。」
大翔は電卓をたたいた。
「$${256}$$や。で、これを$${13}$$でわったあまりは・・・と。」
電卓であまりを直接計算する方法がわからなかったので、ひっ算で解く。
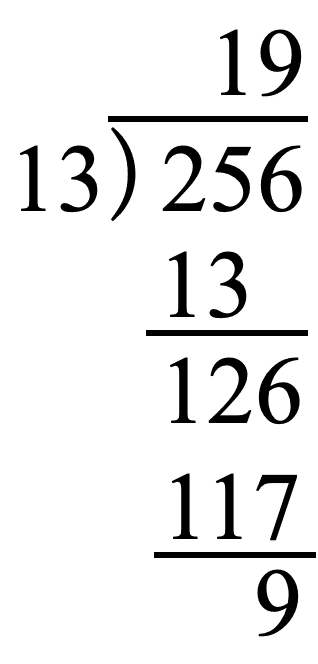
「出ました! あまり$${9}$$っす!!」
「正解!」
吉栄光比売が太鼓判を押した。
「おお〜!」
「ヤバい、めっちゃ気持ちええ!」
大翔は、体の底からわき上がるような興奮を感じた。
数日前、陽菜やケサランパサランに助け舟を出されて解いたときとは、比較にならないほどのカタルシスである。ましてあのときと違い、ターゲットの数字は$${610}$$ケタの化け物だ。たとえて言うなら、体が大きすぎて全身の大半が雲に隠れている巨人の頭に、毛が9本だけ生えていることを看破したようなものだ。さすがのお釈迦様も、「見事」の一言ぐらいは言ってくれるのではあるまいか。すくなくとも、真横にいる女神はちゃんとほめてくれた。
「せっかく解けたんやし、また絵馬で返事しぃ。」
吉栄光比売が袖から未使用の絵馬を取り出した。
「今回は、私はええよ。ぜんぶ大翔が解いたし。大翔が書きぃな。」
「? ええのんか?」
「ええよ、ええよ。」
陽菜が、すこし悲しげに笑いながら言った。
「なんや? 別れ際みたいな顔して。」
「だって、スイーツ食べられへんのやもん・・・。」
「おお・・・。それは悲劇やな。」
何かと思えば、スイーツの話か。心配して損した。
「そう言えば、先方にはなんて返す?」
「へ?」
吉栄光比売の急な質問の意図をはかりかね、大翔は首を傾げた。
「返しの問題や。もう今回はさすがに、答えのわからん問題はやめときや。」
「ああ、そっちっすか・・・。」
この問題を出してきた絵馬の主へ、返しの謎かけをどうするかという話である。
前回は、恥をかかされたことへの逆恨みで無茶な問題を出し、しかもそれを即答で返されてさらに恥をかくという憂き目を見た。今回の問題を見ても、この絵馬の主(仮に“数学徒X”としよう)、かなりデキるようだ。すくなくとも、その辺の高校生よりも数学ができそうな気がする。そんな相手が満足できて、かつ自分でも解ける問題など存在するのだろうか?
めんどうくさいと言ってしまえばそれまでだが、彼は今、問題がほぼ自力で解けて、やや有頂天になっていた。「やられてばかりではないぞ」と数学徒Xに伝えてもやりたい。
大翔が考え込んでいると、吉栄光比売が絵馬を2枚、彼の胸に押し付けた。
「今この場で考えるのは難しいやろし、またしばらく家で考えてみなはれ。」
「うーん。まぁ、そうっすね・・・。」
To Be Continued…
この記事が気に入ったらサポートをしてみませんか?
