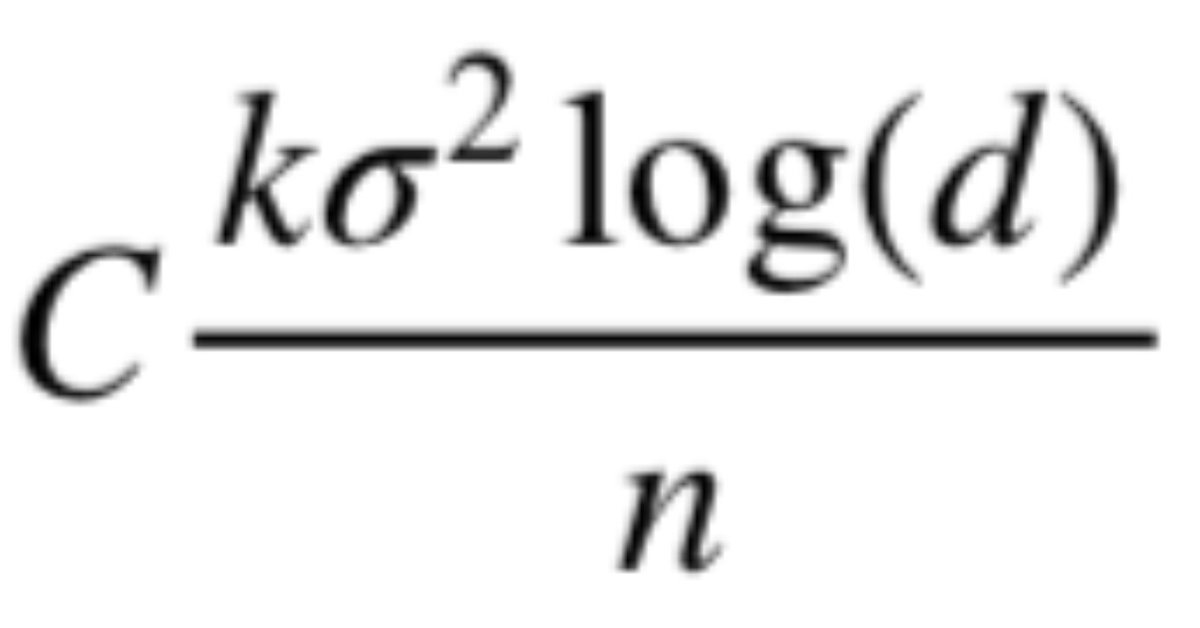
高次元データに対するL1正則化の有効性
Introduction
高次元データでの回帰問題に対して、線形回帰モデルのL1正則化(Lasso回帰)の有効性は広く知られているところです。この有効性の理由は数理統計的な側面からも理解が進んで来ました。代表的な結果の1つに、Lasso回帰の
変数の個数に対して必要なサンプルサイズは対数的にしか増加しない。
と言う性質が挙げられます。今回の目標は、この定理の厳密なステートメントを述べ、数理統計的な証明を紹介することです。
なお、このノートは機械学習の数理 Advent Calendar 2018, 14日目の記事になります。作成者のNoriakiOshitaさんに感謝申し上げます。また当日投稿になってしまったことをお詫び申し上げます。
高次元データに対するL1正則化の有効性について
Introductionで紹介したLasso回帰の性質について、以下のslideで説明しようと思います。
おわりに
せっかくの機会なのに時間の制約のためにだいぶ駆け足になってしまい、制限強凸性の話を詳しくできなかったのが残念でした。本当はoptimizerなどとも関連した話があったり、今回の定理にも別証明や別バージョンが知られていたりしてなかなか奥が深いです。
お正月あたりに改めて、これまで勉強してきたことをもう少し時間をかけて整理し直そうと思います。個人的には、高次元データの統計学・機械学習の数理の「こんなことも説明できるんだ!」という面白さ・強力さがもっと色々な人に伝わったらいいなと思います。それではm(_ _)m
サポートをいただいた場合、新たに記事を書く際に勉強する書籍や筆記用具などを買うお金に使おうと思いますm(_ _)m
