一様最小分散不偏推定量は必ず存在するか？

abstract : 離散型確率分布の場合に、一様最小分散不偏推定量が存在しない例があることを示します。（なお、連続型の場合にも例はありますが、ここでは取り上げません。）

1. Introduction

確率変数 X = (X1, ..., Xn) がパラメータθの確率分布 D(θ) に従っているとします。θの推定量として T := T(X)を準備したとき、以下の2条件を同時にみたすならば一様最小分散不偏推定量というのでした。

1. 不偏性 : θがどんな値であっても、E[T] = θが成り立つ。
2. 一様最小分散性 : θがどんな値であっても、他の不偏推定量Sに比べてTの分散が小さい。要するに、V[T] ≦ V[S] が成り立つ。
※ なお、E[・]は期待値、V[・]は分散を意味します。

一様最小分散不偏推定量とは不偏推定量なかで平均2乗誤差が最も小さいものと言っても同じことです。これは平均2乗誤差のbias-variance分解から分かるのでした。

一様最小分散不偏推定量の例としては、サイズnの独立標本を期待値μ, 分散σ²の正規分布から得た場合、
・期待値μの一様最小分散不偏推定量 = 標本平均
・分散σ²の一様最小分散不偏推定量 = 不偏分散
を示すことができるというものがあります。標本平均はCramer-Raoの定理を用いて、不偏分散はLehmann-Scheffeの定理を用いて示すことができます。

さて上記のように、一様最小分散不偏推定量には様々な有名な例がありますが、「不偏推定量が存在した場合、特に一様最小分散不偏推定量が存在するのか」という疑問への回答はあまり有名でないように見えます。この note では、離散型確率分布の場合で、この疑問に対する回答例 [R] を与えます。

2. 問題

次の問題は「不偏推定量が存在した場合、特に一様最小分散不偏推定量が存在するのか」という疑問に対して、一つの回答を与えてくれるでしょう。

問題 : -1以上の整数を実現値に取りうる確率変数Xが、確率関数

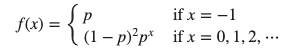
の確率分布に従っているものとします。ただし、p ∈ (0, 1) です。パラメータpを、推定量 T(X) = Σ t[x]1[X=x] (x=-1, 0, 1, 2, ...) を用いて推定する問題を考えてみましょう。ここで 1[A] は 条件Aが真なら1, 偽なら0 を返す関数であるとします。

(1) T(X)が不偏推定量であるとします。このときのt[x]を、t[-1]を用いて表してください。
(2) 分散V[T]をt[-1]を用いて表してください。
(3) 分散V[T]が最小になるようなt[-1]をpを用いて表してください。

問題(1)はpの不偏推定量を全て求めることに対応しています。解く過程で、pの不偏推定量はt[-1]を用いてパラメータ付けできることがわかります。問題(3)はパラメータpの値に応じて、分散が最小になる不偏推定量が異なることを示します。要するに、パラメータpには一様最小分散不偏推定量は存在しないわけです。

3. 問題への解答

(1)への解答 : 推定量Tの期待値 E[T] を p を用いて表してみましょう。ここで、pの次数ごとに項を整理することが重要です。

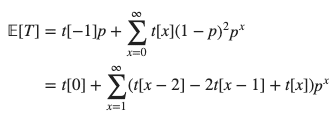
Tが不偏推定量ならば、どんなpの値に対しても E[T] = p が成り立つので、pの1次の項の係数は1, 他の次数の項の係数は0になります。従って、漸化式

t[x] - 2t[x-1] + t[x-2] = 0, t[0] = 0, t[-1] = 定数

を得ることができ、これを解けば t[x] = x(1-t[-1]), (x = 0, 1, 2, ...) を得ることができます。

(2)への解答 : 分散の公式 V[T] = E[T²] - E[T]² を用いましょう。

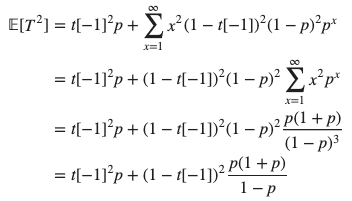
故にTの分散は次のようになります。

(3)への解答 : 分散 V[T] の式を t[-1] について整理すれば、次のような2次関数が現れます。

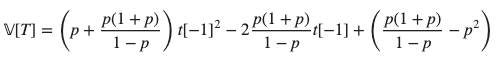
この2次関数が最小値を取るような t[-1] の値をpを用いて表せば良いわけです。平方完成することで次の結果を得ます。

4. 結論

問題(3)からパラメータpの値に応じて分散が最小になる不偏推定量が異なることがわかりました。要するに、パラメータpの一様最小分散不偏推定量は存在しないことが確認できたわけです。

Acknowledgement : この note はnote社の統計勉強会の講師をしているなかで書くに至ったものです。勉強会に参加してくださっている皆様に感謝申し上げます。

References : 
[R] C. R. Rao, "Linear Statistical Inference and its Applications: Second Editon", 1973.