標本中央値は母中央値の不偏推定量か

abstract : 連続型確率分布における母中央値の推定量としての標本中央値を手短に考察します。

Introduction

パラメータθに対して推定量 T(X_1, ..., X_n) を考えたとき、E[ T(X_1, ..., X_n) ] = θ が成り立つならば、推定量 T(X_1, ..., X_n) はパラメータθの不偏推定量であると言います。例えば、標本平均は母平均の不偏推定量です。では、次のような問題を考えてみましょう。

問題 : 連続型確率分布において、標本中央値は母中央値の不偏推定量でしょうか。

Example

次の難しくない例を考えることで、問題の解答が得られます。

問題 : 確率変数 X_1, X_2, X_3 が独立に確率密度関数 f_X(x) = 2x, 0≦x≦1 の確率分布に従っているとします。このとき、以下の問いに答えてください。
(1) 母中央値はいくらか？
(2) X_1, X_2, X_3 の標本中央値Tが従う確率分布の累積分布関数、確率密度関数を求めてください。
(3) 標本中央値Tの期待値 E[T] を求めてください。
(4) 標本中央値Tが従う確率分布の中央値 med[T] を求めてください。

解答 : 
(1) 累積分布関数を F_X(x) と書いたとき、F_X(x) = 0.5 になる値xが母中央値です。F_X(x) = x², 0≦x≦1 なので母中央値は x = √2/2 と分かります。
(2) 標本中央値の累積分布関数は F_T(t) = P[ T≦t ] = 3t⁴(1-t²) + t⁶ = 3t⁴ - 2t⁶, 0≦t≦1です。これを微分することで確率密度関数 f_T(t) = 12t³-12t⁵, 0≦t≦1 と分かります。
(3) E[T] = 12∫_[0, 1] t⁴-t⁶ dt = 24/35
(4) 標本中央値 T の累積分布関数 F_T(t) = 3t⁴ - 2t⁶, 0≦t≦1 について F_T(t) = 0.5 を解けばよい。 この解は t = √2/2 なので、med[T] = √2/2 と分かります。■

この問題の(1)と(3)から E[T]≠母中央値 が得られ、標本中央値Tは母中央値の不偏推定量とは一般に言えないことが分かります。ところで、注目してほしいのは(1)と(4)の比較です。med[T] = 母中央値 は成り立っていそうなことが分かります。

中央値不偏推定量の導入

パラメータθに対して推定量 T(X_1, ..., X_n) を考えたとき、med[ T(X_1, ..., X_n) ] = θ が成り立つならば、推定量 T(X_1, ..., X_n) はパラメータθの中央値不偏推定量 (median-unbiased estimator) であると言います。さて、上の問題は次の定理が成り立つことを示唆しているものです。

定理 : nを正の奇数としましょう。連続型確率変数 X_1, ..., X_n が独立に累積分布関数 F_X(x) の確率分布に従っているものとします。このとき、標本中央値 T(X_1,...,X_n)が従う確率分布の中央値は母中央値に等しい。

証明 : 標本中央値の累積分布関数 F_T(t) は、次のようになります。

tに母中央値を代入したとき、F_T(t) = 1/2になることを示せばよいです。これは F_X(t) = 1/2 が成り立つことに注意すれば、次のように二項定理へ帰着して示されます。

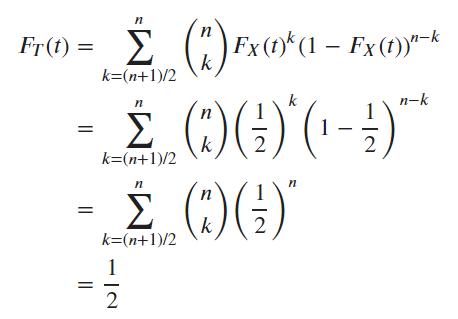
要するに、この定理の条件の下で、標本中央値は母中央値の中央値不偏推定量だとわかりました。■

Acknowledgement : この記事は株式会社すうがくぶんかの社内勉強会での議論を参考に書いたものです。勉強会に参加している講師のみなさんに感謝申し上げます。