標本中央値の場合の中心極限定理

abstract : 標本中央値に対して、標本平均の中心極限定理と同様の主張が成り立つことを紹介します。

1. Introduction

標本平均X̄の代表的な性質の一つに中心極限定理があります。これは「期待値μ, 分散σ²の確率分布からサイズnの標本 X = (X1, ..., Xn) を抽出したとき、統計量 √n(X̄ - μ) が期待値0, 分散σ²の正規分布に分布収束する」というものでした。

このnoteでは、この中心極限定理と同様の主張を標本中央値に対して考えた定理を紹介し、その証明を与えます。

2. 定理の主張

例えば、確率分布Dが標準正規分布の場合は

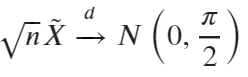
となります。なお、漸近分散が中央値の確率密度に依存している点は特徴的と言えるかもしれません。

Remark : この定理は標本中央値が漸近不偏性、特に漸近正規性をもっていることを主張しています。

3. 定理の証明

step 1. まずは左辺の統計量の確率密度関数を書き下します。

step 2. 次に累積分布関数を中央値まわりでTaylor展開します。

step 3. 極限 n→∞ を取ります。ここでStirlingの公式に注意しましょう。

step 4. まとめ

acknowlegement : 最近アウトプットする機会を作れず反省しています。普段の投稿にスキをくれたり、応援してくれている皆さまに感謝申し上げます。