見出し画像
Photo by ryonakano

進振りにも使われているG.S.アルゴリズムをわかりやすく解説

卯村ウト

はじめに


　東京大学では進学選択(いわゆる『進振り』)が2年の夏休みに行われる。それにより、ほとんどの2年生は3年生から所属する学部学科が決まる。

　さて、その進振りには第一から第三までの段階が存在する。第一段階は各自1つの学部学科しか志望できず、点数順に決まっていく。残念ながらそこで決まらなかった人は、第二段階に進むことになる。

　その第二段階では志望順をつけて複数の学部学科を志望することができる。勘のいい人であればこの時点で気づくかもしれないが、第二段階は第一段階のように単純に点数順で決まるわけではない。つまり、第二段階は単純に点数だけでなく、各々の志望順という要素も反映されるのだ。

　では、第二段階ではどのような採用方法を用いているのだろうか？　もちろん、適当に採用しているわけではない。公平性を期すために、一定のアルゴリズムを採用している。

　そして現在、そのアルゴリズムにはどうやらG.S.アルゴリズムというものが応用されているようだ。これは私が1Sで受講した主題科目『数理工学のすすめ』にて計数工学科の教員が言っていたことなので間違いないと思われる。また、第二段階のアルゴリズムについてネットで調べてみると、『DAアルゴリズム』あるいは『受入保留アルゴリズム』が使われている、と出てくるだろう。DAアルゴリズムも受入保留アルゴリズムもG.S.アルゴリズムの別名である。

　ちなみに、初年次ゼミナールや、英語中級・英語上級の決定にもこのアルゴリズムは使用されている。また、東大に限らず、会社における配属分けなどにもこのアルゴリズムが使用されているようだ。

　そのことを以前Xにポストしたところ、かなりの反響があったので、本記事ではそんなG.S.アルゴリズムについてできるだけわかりやすく解説する。なるべく正確な内容を書くよう心がけるが、私は講義でちょろっと習っただけの初学者なので、もしかしたら誤ったことを書いてしまうかもしれない。そのため、もっと知りたい人やより正確に知りたい人は、自分で調べることをお勧めする。




G.S.アルゴリズムの概要


　G.S.アルゴリズム(Gale-Shapleyアルゴリズム)とは、安定結婚問題における安定マッチングのうち1つ(あるいは2つ)を求めるアルゴリズムである。

　まず、安定結婚問題とは、次のような問題である。


n人の男とn人の女がいて、各々はどの異性と結婚したいかという志望順のリスト(選好リスト)を持っているとする。その人たちで1対1の男女のペアを作るとき、互いに現在組んでいる相手よりも好きであるペアがないような組み合わせ(安定マッチング)を求める問題。


　例えば、図1のようにA〜Eという5人の男と、1〜5という5人の女がいて、各々は、図1のような選好リストを持っているとする。


図1


　この10人で男女1人ずつのペアを5つ作ることを考える。このとき、現在組んでいる相手よりも好きであるペアがないような組み合わせ(安定マッチング)になるようにする。

　例えば、以下の図2のような組み合わせを作るとする。ここで、Cと5に着目してみよう。

　Cは現在第5希望の3とペアを作っているが、5は第1希望である。一方、5は現在第5希望のEとペアを作っているが、Cは第1志望である。つまり、互いに現在組んでいる相手よりも好きであるペアが存在する(Cと5)ことになるので、このマッチングは安定マッチングとはいえない。また、Cと5のようなペアを不安定対と呼ぶ。


図2
青線が不安定対


　つまり、このような不安定対が1つもないような組み合わせ(安定マッチング)を作れるかというのが安定結婚問題である。
　例えば、図3は安定マッチングである。


図3
G.S.アルゴリズムを用いて求めた


　このような安定マッチングは、各々の状況において少なくとも1つ以上は必ず存在する(証明は各自で調べてほしい)。そして、この安定マッチングを1つあるいは2つ機械的に発見できるようなアルゴリズムこそが、G.S.アルゴリズムである。

　G.S.アルゴリズムは、David GaleとLloyd Stowell Shapleyという2人のアメリカ人数学者により考案されたアルゴリズムである。ちなみに、Shapleyは2012年にノーベル経済学賞を受賞している。


G.S.アルゴリズムのやり方(1対1対応の場合)

 

　先の例のように、1対1で対応する場合、G.S.アルゴリズムのルールは実は至って簡単で、以下の通りである。


  1. 全員がペアを作っていない状態で始める。

  2. 片方のサイドに注目する。

  3. ペアを作っていない人Xは、まだ断られていない相手のうち、自分の選好リストの最上位の人Yにプロポーズする。

    1. Yに相手がいないならば、とりあえずXとペアを作る。

    2. Yに相手がいる(つまり他の人X'とペアを作っている場合)ならば以下のように対処する。

      1. Yの選好リストにおいて、XがX'より上位なら、YはX'とペアを解消し、Xとペアを作る。

      2. Yの選好リストにおいて、X'がXより上位なら、YはXのプロポーズを断り、X'とのペアを継続する。

  4. これを繰り返し、全員がペアを作り終えたら終了する。


　では、実際に先の例にG.S.アルゴリズムを適用してみよう。

　ここでは、左の男サイドからプロポーズしていくことにする。まずAが1に、Bが2にCが5にそれぞれプロポーズする。ここまではプロポーズ先が被っていないので、素直にそのまま結べばよい。すると、図4のようになる。


図4


　次に、Dが5にプロポーズするが、5はすでにCとペアを作っている。ここで、5の選好リストを見てみると、Dが3番目なのに対して、Cは1番目である。よって、5はDのプロポーズを断ることになる(図5)。


図5


　そこで、Dは選好リストの2番目の2にプロポーズする。2はすでにBとペアを作っているので、選好リストを参照する。すると、Dは1番目、Bは4番目なので、2はBとペアを解消し、Dと新たにペアを形成する(図6)。


図6


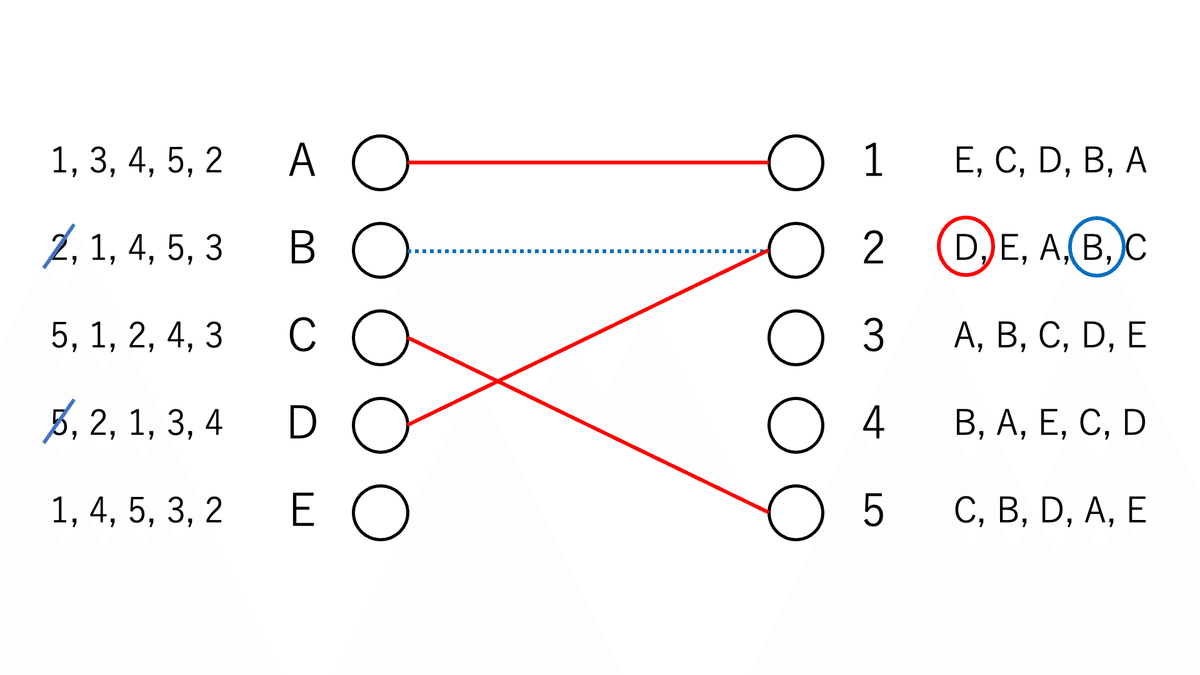
　同様に、Bは選好リストの2番目の1にプロポーズする。1はすでにAとペアを作っているので、選好リストを参照する。すると、Aは5番目、Bは4番目なので、1はAとペアを解消し、Bと新たにペアを形成する(図7)。


図7


　相手がいなくなったAは選好リストを参照し、2番目の3にプロポーズする。相手の3は相手がいないので、Aのプロポーズを受け入れてペアを作る(図8)。


図8


　最後にEが1にプロポーズするが、1はすでにBとペアを作っている。そのため、1は選好リストを参照する。すると、Eは1番目、Bは4番目なので、1はBとペアを解消し、Eとペアを作る(図9)。


図9


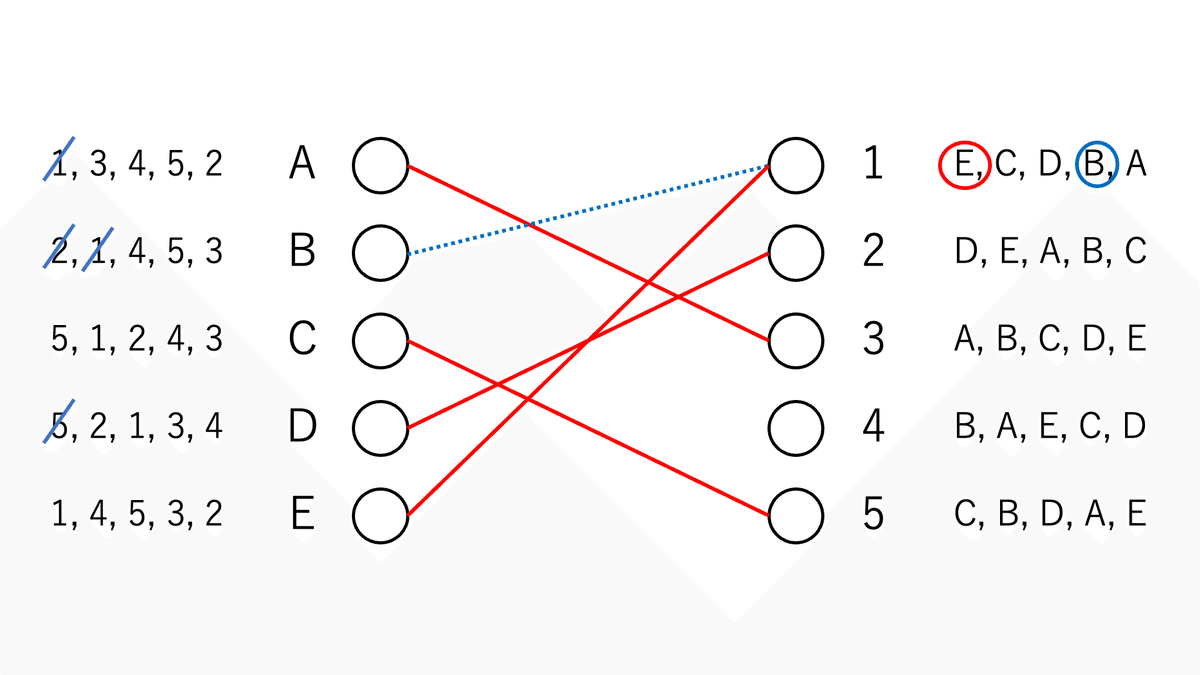
　最後に、相手がいなくなったBは選好リストを参照し、3番目の4にプロポーズする。相手の4は相手がいないので、Bのプロポーズを受け入れてペアを作る(図3)。以上ですべてのペアが完成し、これは安定マッチングとなる。


図3


　いくつか補足をする。

　まず、今回はAから順にプロポーズをしたが、プロポーズする順番を変えても出来上がる安定マッチングは変化しない。気になる人は自分で確かめてみよう。

　また、女性側からプロポーズをしても安定マッチングを出力することができる。一般に、男性側からプロポーズした場合に出る結果と女性側からプロポーズした場合に出る結果は異なるが、今回の例の場合では同じになる(図3)。

　ちなみに、男性側からプロポーズして得た安定マッチングを男性最良安定マッチング、女性側からプロポーズして得た安定マッチングを女性最良安定マッチングと呼ぶ。
　男性最良安定マッチングは男性の希望が最大限に反映された安定マッチングで、女性最良安定マッチングは女性の希望が最大限に反映された安定マッチングである。


G.S.アルゴリズムのやり方(1対1対応でない場合)


　これまで1対1対応する場合を見てきたが、ここからは1対1に対応しない場合、すなわち片側がもう片側よりも数が多く、さらに片側の選好リストがすべて埋まっていない場合を考えてみる。

　例として、図10のような以下の状況を考えてみよう。
　A~Eの5人の学生が、X~Zの3つの学科に進学したいと考える。A~Eはそれぞれの成績と選好リストを持っており、X~Zは点数の高い学生順に選択していく。また、Xの定員は3人、Yの定員は1人、Zの定員は1人とする。


図10
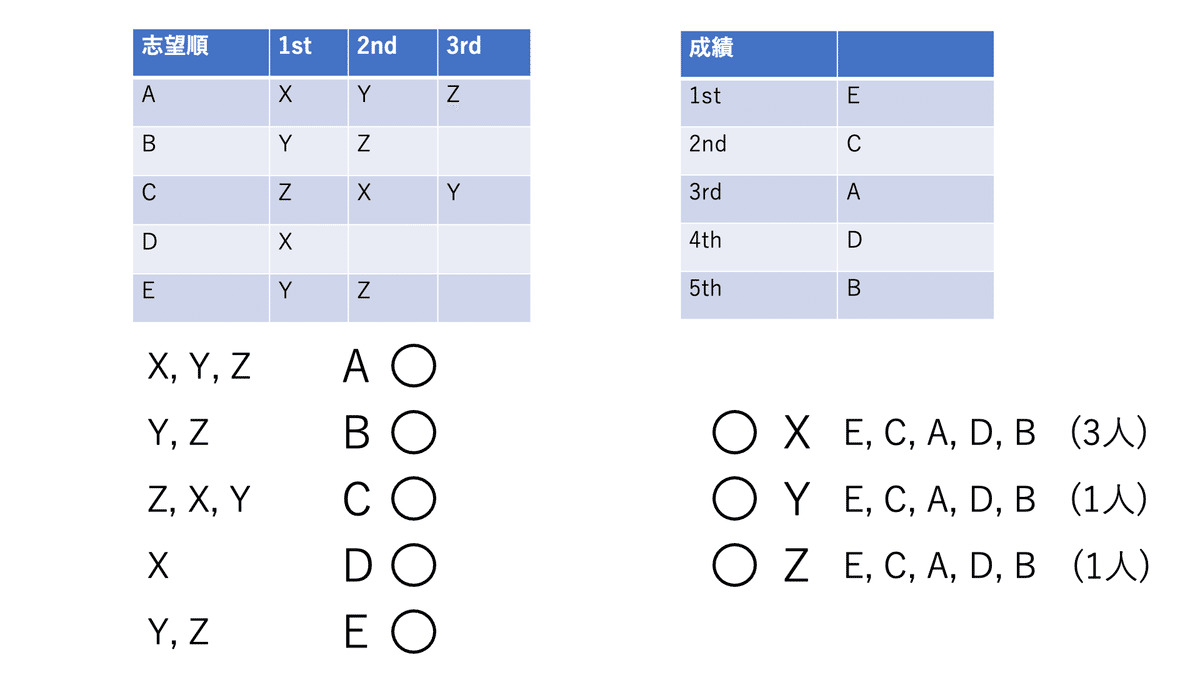
学科側の選好リストはすべて同一となり、学生の成績順となる


　先ほどの例とはかなり状況が異なるが、アルゴリズムの中身自体はほとんど同じで、以下の通りとなる。


  1. 全員が進学していない状態で始める。

  2. 生徒サイドに注目する。

  3. 進学していない人Pは、まだ断られていない学科のうち、自分の選好リストの最上位であるQ学科に進学しようとする。

    1. Qが定員に満たなければ、とりあえずPを受け入れる。

    2. Qが定員いっぱいならば以下のように対処する。

      1. Qの選好リストにおいて、Pが現在入っている人のうち最下位であるP'より上位なら、QはP'を追い出し、Pを入れる。

      2. Qの選好リストにおいて、P'がPより上位なら、QはPの進学を断る。

  4. これを繰り返し、できなくなったら終了する。


　では、実際に先の例にアルゴリズムを使用してみよう。

　まず、AがX、BがY、CがZ、DがXに入ろうとする(図11)。X~Zはまだ定員に満たないので、全員を受け入れる。


図11


　次にEはYに進学しようとする。しかし、Yは定員1名であり、すでにBが入っている。ここでEとBの成績を比べると、Eの方がBより成績が良いため、BはYを追い出され、代わりにEが入ることになる(図12)。


図12


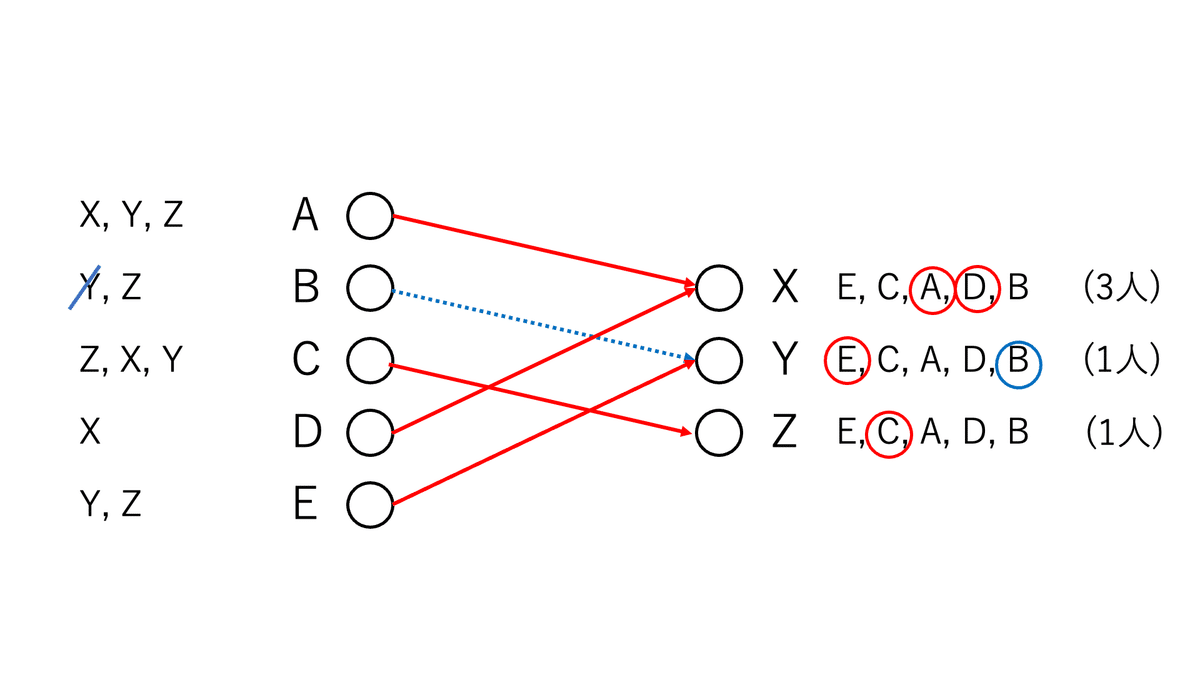
　次に、Bは選好リストに従いZに進学しようとする。ただし、Zは定員1名であり、すでにCが入っている。ここで、BとCの成績を比べると、Cの方がBより成績が良いため、BはZに入れない(図13)。


図13


　Bはもう選好リストが残っていないので、ここでマッチングは終了となる。少々物足りない感じがするが、完成した組み合わせ(図14)を見てみると、安定マッチングになっていることがわかる。


図14
安定マッチングの定義は、不安定対が1つもないような組み合わせである。


　ここでもう気づいた人も多いかと思うが、この例はほとんど進振りの第二段階のシステムと同じである。この例でいえば、Bは第二段階で内定せず、第三段階へと進み、X学科は第三段階で枠を設けることになるだろう。
　ただし、実際の進振りでは、学部学科ごとに使う点数が異なったり、工学部の場合は志望理由書が考慮されたりなど、これ以外にさまざまな要素がある。そのため完全な同一視はできないが、概ねこのような仕組みによって成り立っているといえる。

　さて、この例では学生側からアプローチをしていた。そのため、1対1のときの例で述べたように、これは学生側の希望が最大限配慮された安定マッチングである。つまり、もし進振り第二段階に進んだときは、自分の志望順を正直に、志望する可能性のある学科をすべて書くことが最適であるということだ(ちなみにこのことは第二段階を選ぶときUTASに注意書きとして表示されるので、学生側からマッチングをするのは確実だと思われる)。

　実際、私も第一段階の底点が84点台だった理学部情報科学科に、第二段階の第一志望で書いたところ、77点台で(奇跡的に)通ったので、変に考えを巡らせることなく、自分に正直に書くのが良いと思う。


　

おわりに


　ここまでG.S.アルゴリズムについて解説してきたが、もっと詳しく知りたいという人は、以下に示す参考サイトを見たり、自分で調べたりしてほしい。また、本記事の内容に誤りがあれば、下部のコメント欄やXのポストに反応してほしい。


G.S.アルゴリズムについての他の記事(参考サイト)



この記事が気に入ったらサポートをしてみませんか？