渋滞の原因

【はじめに】

渋滞は渋滞学という比較的新しい学問で研究されています。

その中からメジャーな原因をピックアップします。

【渋滞の原因ランキング】

年間の渋滞ランキングでは以下のようになっています。

1位 交通集中 53%
2位 事故 24%
3位 工事 6%
-位 その他 17%

そのうち多くを占める交通集中の内訳は以下のようになっています。

サグ部および上り坂など 52.7%
接続道路からの渋滞など 38.9%
インターチェンジ等の合流 7.5%

ほとんどが上り坂を起因とした自然渋滞であることが読み取れます。

お盆で単に交通量が多いから接続道路やインターチェンジでの渋滞が多いかと思いきや、道路の起伏に起因しています。

出典:渋滞ランキングのとりまとめ（平成 28 年 年間・GW） 国土交通省
http://www.mlit.go.jp/common/001178087.pdf

【サグ部とは】

事故や工事の渋滞は想像が付きやすいですが、サグ部というのは渋滞の主要因にも関わらず非常にマイナーな用語です。

サグというのは高速道路の緩やかな坂道です。

英語でsagというのは、本棚等にモノをおいておくと重みで本棚がたわんだ状態になったことを表す言葉です。

緩やかさが伝わるでしょうか？

この緩やかというのがやっかいで、ドライバーが気が付いた時には速度が低下しているという現象を引き起こします。

この気が付かない減速を行った車の後ろの車は追いつきブレーキを踏みます。

その車のさらに後ろの車はより大きな減速を行うことになり、後ろに伝搬するに連れてどんどん速度と車間距離は小さくなり、最終的には止まってしまうほどの渋滞を引き起こします。

高速道路運営会社はこのことをよく承知しているので、「登り坂速度低下注意！」といった看板を置いて自然渋滞の抑止を狙っていますが、直近の統計結果を見てもなかなか解消は難しいことがわかります。

【料金所渋滞はどうなったのか？】

ETCの普及で料金所渋滞は随分緩和されました。

ETC導入前の平成12年では渋滞の32.1%が料金所（渋滞要因のトップ）でしたが、平成20年では0.8%まで低下しています。

DSRC→ETC2.0は振るいませんが、ETCそのものはかなり普及しています。

平成24年のデータですが、
自動車保有台数に占めるETC装着台数は50%
高速道路利用台数におけるETC装着台数は88%
もあります。

出典:ETCの利用状況、導入効果等 国土交通省
http://www.mlit.go.jp/road/ir/ir-council/pdf/7.pdf

【渋滞の経済損失】

平成17年実績で年間11.7兆円の損失が出ているみたいです。

時間にすると35.1億人時間。

時給3333円換算なのでちょっと平均年収よりは高めの算段ですね。

交通マヒが起こることで発生する他の損害（緊急車両が通れなくなる等）も入っているかもしれませんが。

出典:効果的な渋滞対策の推進 - 国土交通省
http://www.mlit.go.jp/road/ir/ir-perform/h18/07.pdf

【渋滞の科学】

渋滞は科学的には自己駆動粒子の動き方で説明されます。

セルオートマトン法のモデルの一つ、ASEP（エイセップ）を用いると数学的な説明ができるようになります。

もともとはイスラエルの科学者がタンパク質合成モデルとして考え出したものですが、車一台一台を粒子としてモデル化するのと、とても相性が良いです。

ASEPはAsynmetric Simple Exclusion Process（非対称単純排除過程）の略です。

非対称は一方向にしか進まないという意味です。
単純はそのまま。
排除は排除体積効果の略で、モデル化した時に重ならないことを意味します。

道路を離散的な空間（画面のドットのようなもの）に置き換え、車がその中を同一方向に同時に移動するが、前の車がいるときには移動できない（排他性）という形でシミュレーションします。

そうすると面白いことに、渋滞が起こる道路内の車の密度0.5を上回ると渋滞し、その渋滞は実際の渋滞と同じように後ろに伝搬するように動きます。

出典:渋滞学 西成活裕著（新潮社 2006年発行）

【ASEPによるシミュレーション例】

シミュレーションとはいえ、別にコンピュータを使って高速・大規模にやらなくても出来ます。

数学的に説明できるとは言え、皆さん学者では無いのでそこまで厳密にする必要はありません。

面白いのでちょっとやってみてみましょう。

〈基本的なルール説明〉

離散的な箱を用意します。

箱が道路です。

箱（=道路）に車を置きますが、車を描くのがめんどくさいので●にします。

一方通行で進みますが、ここでは→の向きで進ませます。

置いた車は一度にひとマスぶん一斉に動きます。
ただし、前の車に重なったり飛び越えたりは出来ません。

言葉だけだと分かりづらいので図を載せます。

〈動かしてみよう〉

渋滞では無い混雑していない交通を想定します。

道路のセル18個に対して車は7台です。

密度は7/18≒0.39です。

便宜的に右端と左端を繋げてループさせる事で密度を保ちます。

右端に飛び出した車は左端に飛び込んできます。

ステップ1の段階では部分的に詰まっている状態がありますが、ステップが進むに従って混雑が解消され最終的には止まる車は無くなります。

〈渋滞を再現してみる〉

今度は渋滞を起こしてみましょう。

道路のセル18個に対して車は10台です。

密度は10/18≒0.56です。

先ほどと同じように便宜的に右端と左端を繋げてループさせます。

灰色になっているセルに注目すると、詰んでいる車の列が後ろに移動している事が分かります。※車1台1台は前にしか進んでいません。

実際の渋滞でも交通量そのものが解消されない場合は後ろに伝搬するので、リアルに再現する事が分かります。

【渋滞の基本図】

渋滞を分析するときに流量と密度の関係を表すグラフで見ると分析がしやすくなります。

この軸を持ったグラフを基本図といいます。

【プラトーン走行】

車は前の車と同時に動くことが物理的には可能です（精神的に無理ですが）。

自動運転の実証実験の一つに隊列走行（プラトーン走行）というものがあります。
これは短い車間距離を維持したまま、前方の車両に後方の車両がついていくというものですが、実用化されれば先頭のドライバー一人で大量のトラックを引き連れて列車のように走ることができます。

自動運転についてはこちらのノートを参照してください。

【メタ安定状態】

ASEPの実験では直前に目の前にいた車と同時には動くことができないので、前のスペースが現れるまで後ろの車は待つことになります。

しかし実際の車は渋滞が起こる直前、人は渋滞を起こさせまいと努力するのでプラトーン走行に近い走行をして、なんとか止まるまいとします。

この状態は密度がオーバーしているのでいつ止まってもおかしくない状態でメタ安定状態といいます。

グラフは特徴的な形をしていて漢字の「人」という字に似ています。

渋滞学の筆者の目の付け所はこの現象を物質の相変化（固体→液体→気体）に当てはめていることです。

振動を加えず（刺激を与えず）ゆっくり冷却したジュースがグラスを注ぐときの衝撃で凍ってシャーベット状になる現象を見た人も多いと思います。

この現象は過冷却と言って、液体なのに凍るときの温度を下回っています。

【メタ安定状態の崩壊する実験映像】

たまにテレビでやっている渋滞の実験映像です。

サークル状のサーキット走行でブレーキランプが点くと、それまで走っていた車が全て止まってしまうというものです。

これは、ブレーキランプが渋滞を作っているかのように誤解されていますが、もともと密度が高い状態（道の長さに比べて車が多過ぎる）を作っているので、実際の現象とは違います。

飽和していて、いつ止まってもおかしくないという状態でもなんとか動くことが出来るが、ほんの些細なきっかけでやはり止まってしまうことを証明した実験映像です。

【2車線の渋滞】

これもたまにTVでやっていますが、2車線の高速道路で渋滞すると、追越車線の方が遅いです。

これは人が渋滞になりそうなことを察知すると走行車線から追越車線に入る車が多くなり、結局追越車線の密度が高くなるので混雑してしまうということになるからです。

トラックなどの職業ドライバーにとってはよく知られた話だそうです。

グラフはとある高速道路の丸一日の車線ごとの混み具合を表したものです。

【ASEPの拡張】

ASEPは面白いモデルですが、とても単純なモデルなので、現実とはかけ離れています。

ASEPの基本図を書くと図のようになります。

実際の基本図とはやはり違った形をしています。

以降にASEPに現実に近い車の挙動をルールとして追加してみます。

〈見通しモデル〉

現実の車は前の車が動き出す前から、前の車の動きだけではなく、信号や前の車の窓ガラス越しに見える前の前の車の動きを見ています。
（そして発進時の追突事故を起こしたりします）

それをモデル化したのが見通しモデルです。

前の前の車の前に空きスペースがあれば前の車と同時に前に出ます。

〈見通しモデルの基本図〉

全体的に交通流量が増えて、限界密度も上昇しています。

〈スロースタートモデル〉

今度は前の車が発進してもすぐには発進せず、1回休んでから発進します。

トラックなどの大型車は発進が遅いので、このような動きになります。

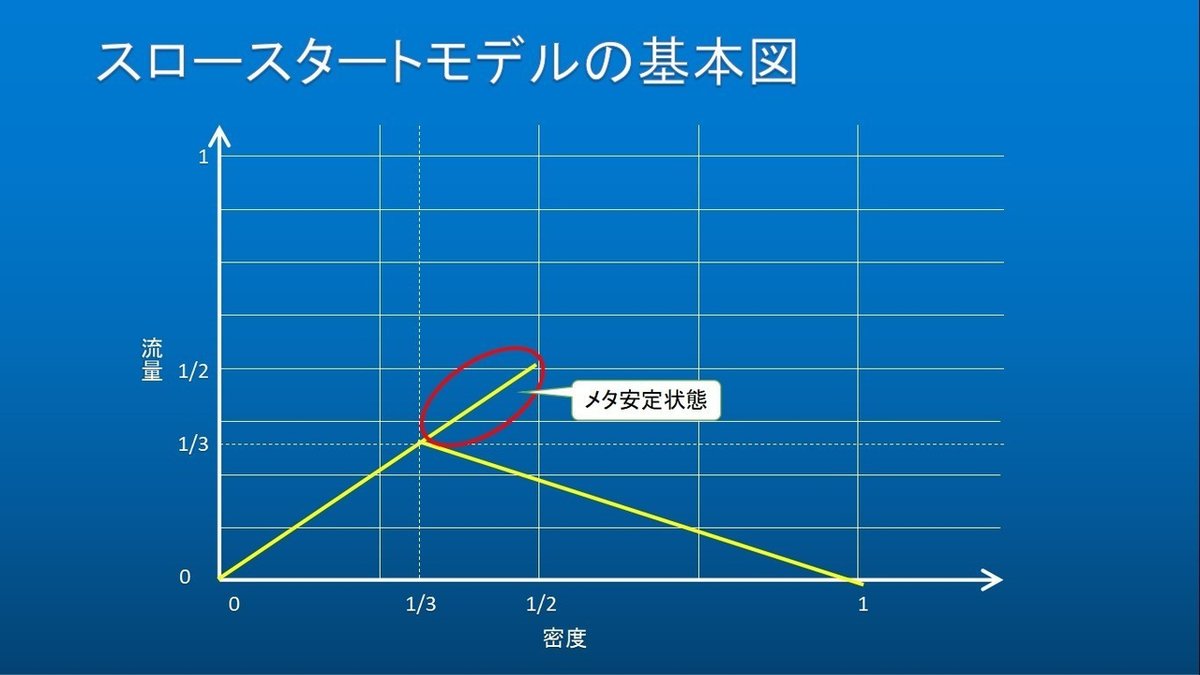
〈スロースタートモデルの基本図〉

限界密度や交通流量は下がっていますが、メタ安定状態を作っています。

【渋滞学の面白いところ】

分野横断的にさまざまなものに渋滞を当てはめているところが面白いです。

気体の動きや、石積みのアーチ橋などにも当てはめています。

おかげでツムツムをやっていて隙間があると（渋滞が起こっている）と密かに思ったりもします。

話が逸れました。

現実のシミュレーションができてくると、今度はどれだけ渋滞を減らす余地があるのか、何がボトルネックになっているのかが見えてきます。

【あとがき】

渋滞は誰も得しません。

走っている人も周りにいる人も良いことはひとつも無いです。

車で走っていて本人の努力ではどうしようもない、コントロール不可能な不利益なためストレスがたまります。

よく渋滞に巻き込まれるという表現をしますが、基本的に交通の集中から起こる問題なので、巻き込まれている人も渋滞を作っている一因になります。

なので、渋滞には「参加する」という表現のが的確かもしれません。

この表現は他人から不利益を押し付けられている感覚が減り、当事者意識が出て少しだけ気分が楽になります。

ま、それでも参加したくはないものですね。