Stan・Rstan練習

目的

　StanとRStanの練習として，それぞれ20試行の再認課題1（Q1）と再認課題2（Q2）について参加者間条件（A，B）で課題成績に差があるか調べたかった。次に再認課題成績のヒストグラムを示す。それぞれについてほぼほぼ満点（20点）に近いデータを作成した。

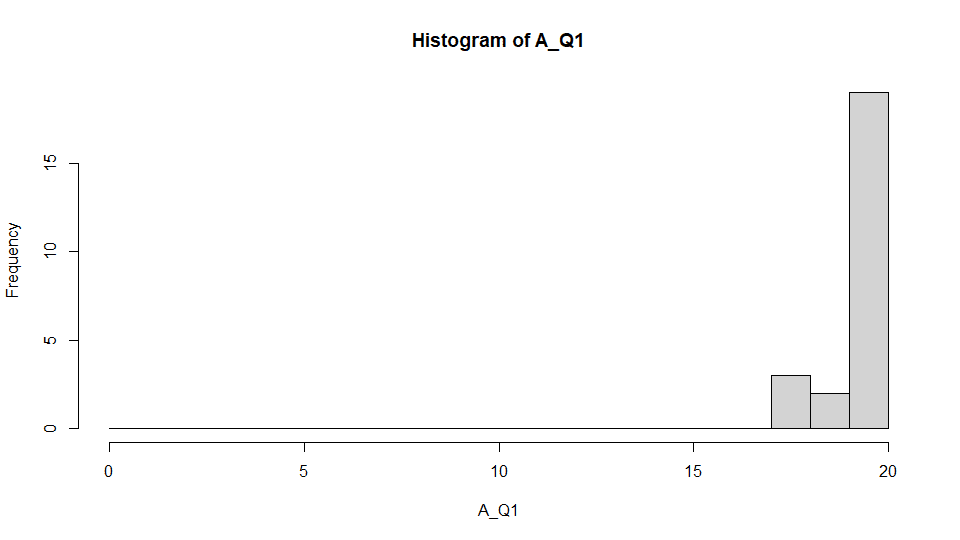
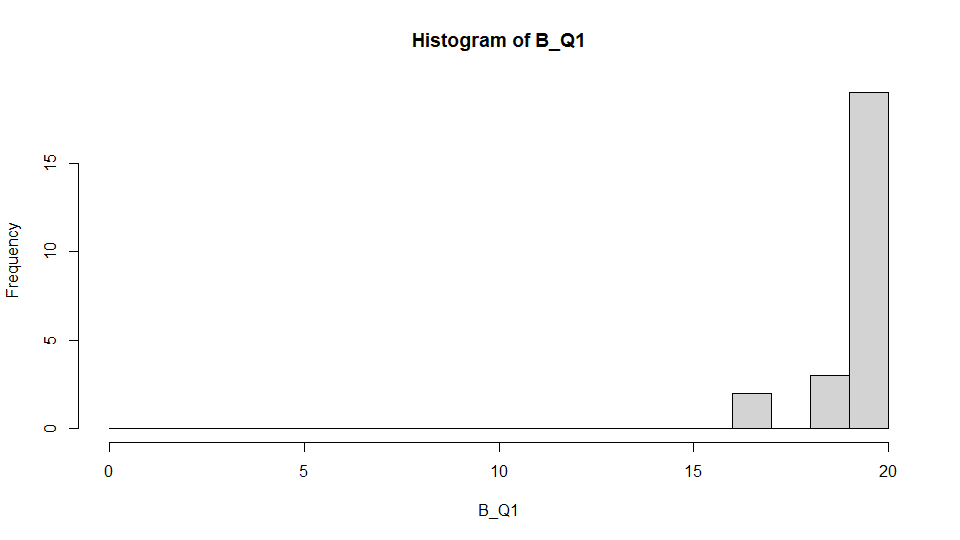
正規分布であてはめてみる1

　とりあえず大好きな正規分布を用いたモデルをあてはめてみる。以下のStanコードを用いた。

//normal.Stan
data {
 int N; //条件毎の参加者数
 int<lower=0, upper=20> A_Q1[N]; //条件Aの人の再認課題1の成績
 int<lower=0, upper=20> A_Q2[N]; //条件Aの人の再認課題2の成績
 int<lower=0, upper=20> B_Q1[N]; //条件Bの人の再認課題1の成績
 int<lower=0, upper=20> B_Q2[N]; //条件Bの人の再認課題2の成績
}

parameters{
 real A_1; //条件Aの人の再認課題1の成績についてのパラメータ
 real A_2; //条件Aの人の再認課題2の成績についてのパラメータ
 real B_1; //条件Bの人の再認課題1の成績についてのパラメータ
 real B_2; //条件Bの人の再認課題2の成績についてのパラメータ
 vector[4]<lower=0>  sigma; //分散なので下限0
}

model{
 for (n in 1:N){
   A_Q1[n] ~ normal(A_1, sigma[1]);
   A_Q2[n] ~ normal(A_2, sigma[2]);
   B_Q1[n] ~ normal(B_1, sigma[3]);
   B_Q2[n] ~ normal(B_2, sigma[4]);
 }
}
​

正規分布であてはめてみる1-結果

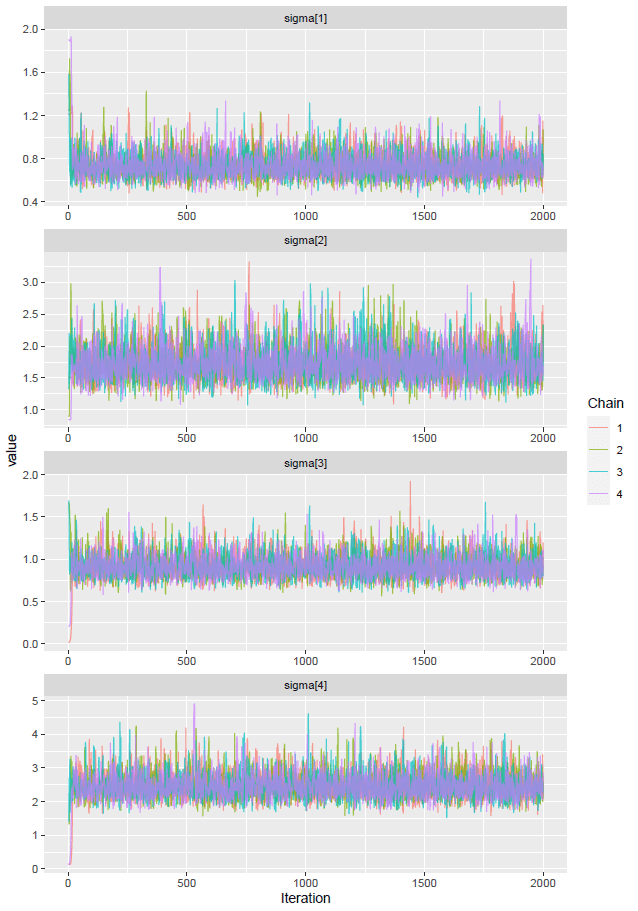
　確認した感じ，各パラメータは収束していそうである。各パラメータの値は次の通りであった。 ​

mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
A_1       19.66    0.00 0.15  19.35  19.56  19.66  19.76  19.92  2772    1
A_2       18.51    0.01 0.38  17.77  18.26  18.50  18.74  19.26  1476    1
B_1       19.62    0.00 0.18  19.25  19.50  19.62  19.74  19.93  2915    1
B_2       17.94    0.01 0.53  16.89  17.60  17.92  18.29  19.00  3030    1
sigma[1]   0.74    0.00 0.12   0.55   0.66   0.73   0.81   1.01  2642    1
sigma[2]   1.75    0.01 0.28   1.30   1.55   1.71   1.91   2.41  2065    1
sigma[3]   0.92    0.00 0.15   0.69   0.82   0.90   1.01   1.27  2602    1
sigma[4]   2.49    0.01 0.39   1.86   2.21   2.44   2.73   3.39  3253    1
lp__     -72.40    0.08 2.48 -78.14 -73.71 -71.97 -70.63 -68.87   911    1

正規分布であてはめてみる2

　1では，参加者間条件×再認課題の4条件毎にパラメータを設定し，フィッティングを行ったが，回帰分析的なものをしたくなった。以下のStanコードを用いた。

data {
 int N;  //データ数
 int ID; //参加者番号
 int C;  //条件
 int<lower=0, upper=20> Score[N]; //再認課題成績
 int<lower=0, upper=1> P[N]; //参加者間条件A or B
 int<lower=0, upper=1> R[N]; //再認課題1 or 2
}

parameters{
 real a; //切片
 real b; //参加者間条件の効果
 real c; //再認課題の効果
 real d; //参加者間条件と再認課題の交互作用
 vector[ID] sigma_within; //個人内の分散になってない，なにこれ
 vector<lower=0>[C] sigma_between; //参加者間条件間の分散
}

transformed parameters{
 real Score_base[N];
 
 for (id in 1: ID){
   for(n in 1:N){
      Score_base[n] = a + b*P[n] + c*R[n] + d*P[n]*R[n] + sigma_within[id];
   }
 }
}

model{
 for (n in 1:N){
   Score[n] ~ normal(Score_base[n], sigma_between[C]); 
 }
}

正規分布であてはめてみる2-結果

　これが...収束なのぉ？
なお，参加者間で分散を等しくした場合には以下のような結果が得られた。

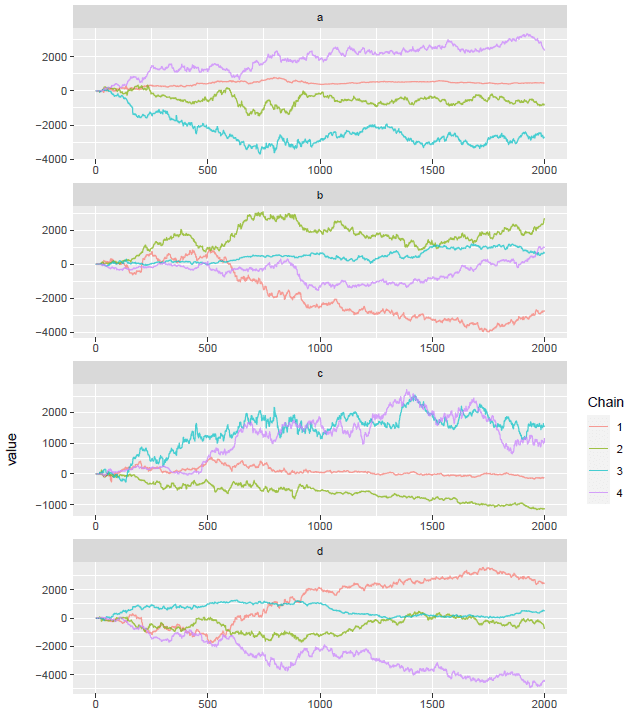
　なんか散らされてるよぉ！

二項分布であてはめてみる

　そもそもデータの性質と散布図を見るからに，パラメータの収束有無に関わらず正規分布を用いていることが問題である。逆に言うと，パラメータが収束したモデルなら使っても大丈夫という話でもないんだなと思った。さらに加えて言うと，先の二つのモデルでは予測値として20点を超える値がばんばん出て来ることも問題である。そこで，遅まきながら二項分布を用いたモデルを作成した。以下のStanコードを用いた。

data {
 int N;
 int<lower=0, upper=20> A_Q1[N];
 int<lower=0, upper=20> A_Q2[N];
 int<lower=0, upper=20> B_Q1[N];
 int<lower=0, upper=20> B_Q2[N];
}

parameters{
 real<lower=0, upper=1> a_1;
 real<lower=0, upper=1> a_2;
 real<lower=0, upper=1> a_1;
 real<lower=0, upper=1> a_2;
}

model{
 for (n in 1:N){
   A_Q1[n] ~ binomial(20, a_1);
   A_Q2[n] ~ binomial(20, a_2);
   B_Q1[n] ~ binomial(20, b_1);
   B_Q2[n] ~ binomial(20, b_2);
 }
}

　パラメータはデフォルト設定だと-2～2の一様分布からサンプリングされるので，確率パラメータを宣言する際には，<lower=0, upper=1>とパラメータ値の範囲を指定しておかないとエラーを吐かれる。

二項分布であてはめてみる-結果

　どうやら収束していそうである。各パラメータの値は次の通りであった。

       mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
a_1     0.98    0.00 0.01    0.97    0.98    0.98    0.99    0.99  2858    1
a_2     0.92    0.00 0.01    0.90    0.92    0.92    0.93    0.95  3740    1
b_1     0.98    0.00 0.01    0.96    0.98    0.98    0.98    0.99  2981    1
b_2     0.89    0.00 0.01    0.87    0.89    0.89    0.90    0.92  4584    1
lp__ -375.63    0.03 1.43 -379.39 -376.28 -375.28 -374.58 -373.89  1776    1

　信頼区間のかぶり具合から，A，Bの両条件で再認課題1の成績＞再認課題2の成績であったらしい。また，再認課題1の成績はAB間で変わらないが，再認課題2の成績はA＞Bっぽい。とは言っても20*0.03＝0.6問分の差でしかないので，意味があるかというと分からない。