最低限が現実:一般相対論/Einstein作用

前回までで，曲がった時空を記述する数学的な準備が終わった．今日はおさらいのあと，今の物理学で最も成功している重力理論の作用と運動方程式を紹介しようと思う．

計量，共変微分，曲率

重力の影響は，全て座標変換(観測者の見方)に吸収できるという原理を受け入れると，時空が曲がることがわかった．曲がった時空を記述する方法として次のものを用意したのだった．

おさらい部分は過去記事にもう少し詳しく書いてある．

計量
計量"g_μν"とは時空の各点に定義された，長さを決めるための物差しだった．

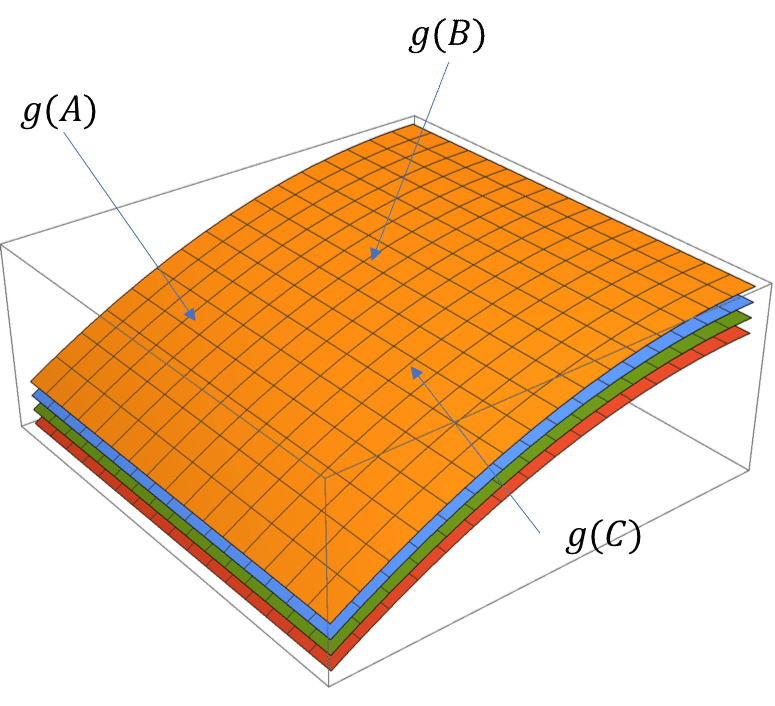
我々は時間と空間の四次元に住んでいるので，計量"g_μν"の足，μとνは0,1,2,3の四つの値をとるのだった．

共変微分
曲がった時空では曲がっていることから普通の微分が意味をなさない．矢印を曲がった時空に沿って平行移動するという概念から共変微分"∇"を決めたのだった．

普通の微分"∂"と曲がった時空の平行移動の効果を取り入れる接続"Γ"を使って共変微分を作った．

曲率
平行移動のために作った接続は，座標(見る人)に依る量だった．時空の曲がり具合を座標に依らない(誰から見ても同じ)量を決めたい．それが曲率だった．ある点から別の点に矢印を平行移動するときに異なる経路を取らせた二つの矢印の差から曲率を見いだせる．

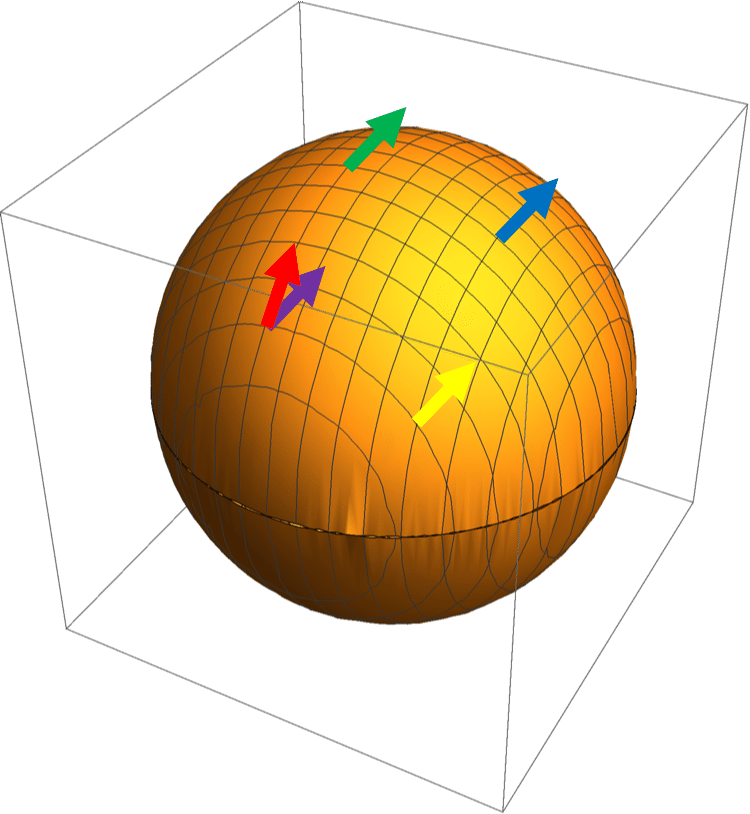
矢印青から青>緑>赤と行ったものと青>黄>紫と行った赤と紫の矢印の差を比べる．

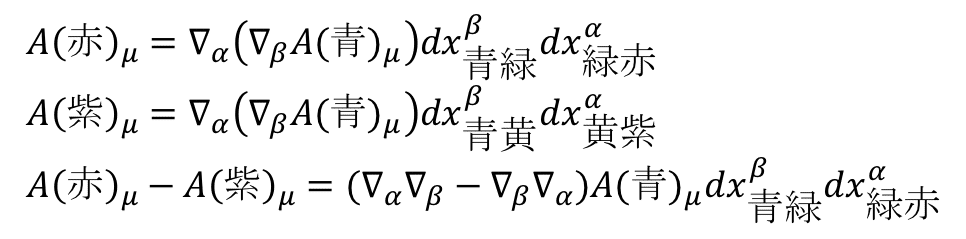
最後の行，二つの共変微分の差が曲率"R"

と決めた．これは座標に依らない時空の曲がり具合を示すものだった．

最小作用の原理

物理の世界では物体の運動を決める時に二つの方法があるのだった．一つはその瞬間から次の瞬間にちょびっと運動がどのように変化するかを記述するもの．これは運動方程式というものだった．もう一つは運動全体(経路)を決めて初めて決まる，作用というものが最小になるように決める方法だった．

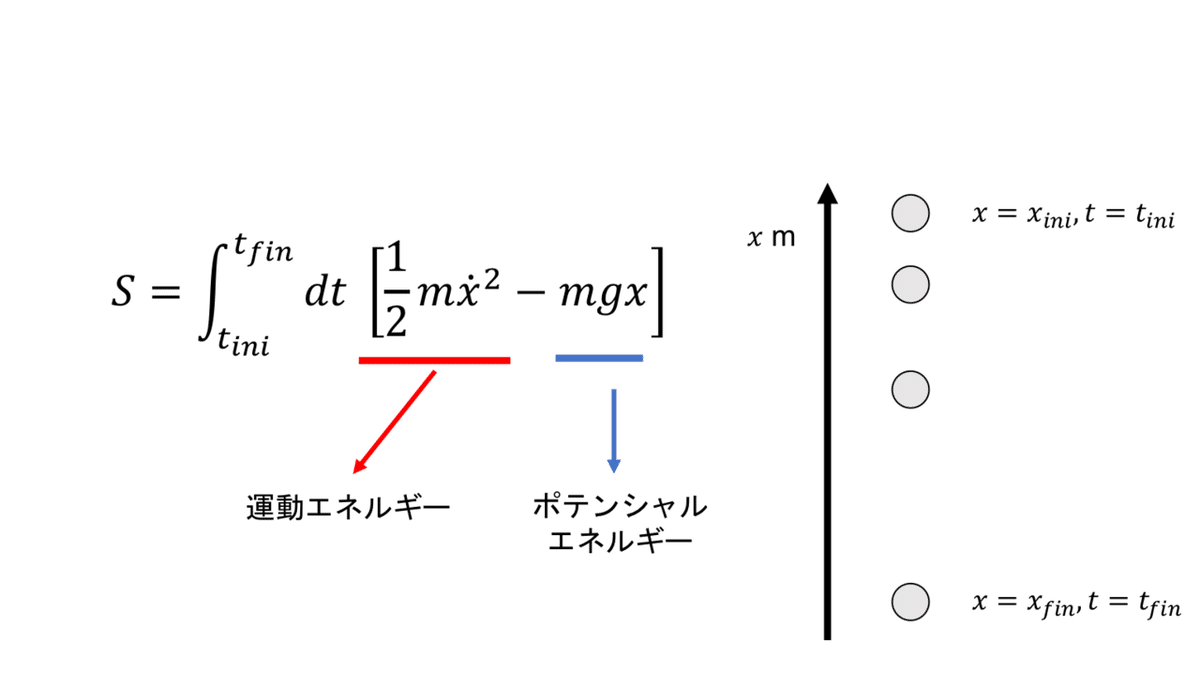
例えば上は，落ちる物体の作用だ．

作用を決める運動の経路をちょびっと変化させて作用のちょびっと変化を見る．

上の絵は経路をちょびっと変化させたイメージだ．

その経路のちょびっと変化で起こる，作用のちょびっと変化"δS"が0になるような時，作用が最小になる経路なのだ．

実は，最小作用で決まる運動と運動方程式で決まる運動は全く同じものだった．なぜなら最小作用の原理と運動方程式は互いに互いを導けるからだった．

一番簡単な重力の作用

では重力によって曲がる時空は，どのように決められるのだろうか．もう話の流れからわかるだろう．重力を使って決められる"作用"を何か決めてしまえばいいのだ．

作用は(人間が解る書き方では)積分の形で書かれている，ただの数だ．曲がり具合の決める作用にしたいわけだから，きっと曲率"R^μ_ναβ"を使って書くのだろう．曲率はμ,ν,α,βの足を持ったテンソルだから，これをただの数にしたい．

使える量は，計量"g_μν"と共変微分"∇_μ"，曲率"R^μ_ναβ"だ．パッと思いつくのは曲率の足の和をとって潰す方法だ．

とりあえず一番目と三番目の足で和をとったものをリーマンテンソルという．何で一番三番なのかというのは実は理由がちゃんとあるのだが，割愛する．ざっくりいうと意味のある和の取り方がこの一つしかないのだ．

これを更に和をとる．

和は上と下でとるので今度は計量gととる．このただの数字"R"はリッチスカラーという．

ではただの数ができた．作用はどうなるだろうか．パッと思いつくのはただのR積分だ．

"d^4x"というのは時間と空間四次元で積分しろというマークだ．dtdxdydzと一々書いていると面倒だから省略して書く．

しかしこれはだめだ．なぜかというと積分が座標にもろによっている．これを解消するには，積分測度(物差しの補正)が要る．物差しの補正を入れて一番簡単なのは，

"√g"が積分測度で，ただの数"Λ(ラムダ)"が入っている．これが一番簡単なものだ．物質があればその分の効果"L"が次のように入る．

ただの物質との重力の効果は"√g"と，"L"の中の微分が共変微分になることで取り入れられる．

実はこの超単純に出された，この作用が現実の重力理論になっている．宇宙観測でとんでもない精度で一致している．

次回から，運動方程式を出して，ブラックホールや重力波を見てみたい．

touya_Y のお話物理｜touya｜note