プランク関数からウィーンの変位則を導出し、太陽のピーク波長を求める。

プランクの法則において、黒体から輻射される電磁波の分光放射輝度は、周波数 ν と温度 T の関数として

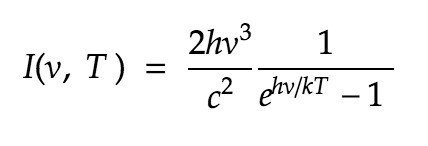
と表すことができる。ただし、ここで分光放射輝度 I (ν, T) は、放射面の単位面積、立体角、周波数あたりの放射束を表しており、h はプランク定数、k はボルツマン定数、c は光速度を表す。分光放射輝度 I(ν, T) は hν = 2.82 kT の位置にピークをもち、高周波数においては指数関数的に、低周波数においては多項式的に減少する。

またプランクの法則において、分光放射輝度は波長 λ の関数として

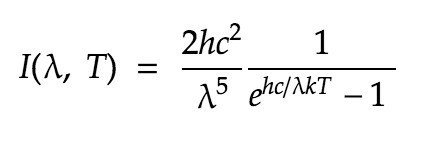
という形であらわすこともできる。 ここで波長と周波数は λ = c/ν という関係式によって結びついている。この関数は hc = 4.97 λkT の位置にピークをもつ。これはウィーンの変位則でより一般的に用いられるピークである。
(wikiより引用)

プランク関数を微分してウィーン の変位則を、積分してステファン・ボル ツマンの法則を計算する。

1. ウィーン の変位則
I(ν, T)を微分する.

この式をグラフに表すと以下の通りとなる
(縦軸にf横軸にx)