無音が音を持つとき、アート作品が生まれた。眠れない夜の話

アートができる過程

　完成形だけ見ても、なんでそうなったのか、理解できないことも多いアート。そんな中、鈴木康広さんの『まばたきとはばたき』では、作品がどういう着想から昇華して形作られたのか、作者自身によってかわいいイラストと共に紹介されている。

まばたきとはばたき

　久しぶりにこれを読み返していて、ふと大学時代の、ある眠れない夜のことを思い出した。

　その日のことを思い出しながら書こうと思う。

無音が「音」を持つとき

　僕は京都の下宿で、一人ベッドに横たわっていた。暑かったのか、全然寝付くことができず、寝返りを繰り返していた。

　耳をすませてみた。住宅地に位置する僕の家からは、外を走る車の音も聞こえず、ただ静寂が夜を包んでいた。それでも、辛抱強く耳をすませていると、ぼーっとした無音の質感が音を持ちはじめた。

　「レ」だ、と思った。

　僕には絶対音感はないが、当時はギターを必死に練習していたので、なんとなく音階がわかった。研ぎ澄まされた無音の空間から聞こえてきたのは、まちがいなく「レ（D）」の音だった。

音階を図で考えてみる

　僕は頭の中で、円形の図における、音の位置関係をイメージしてみた。

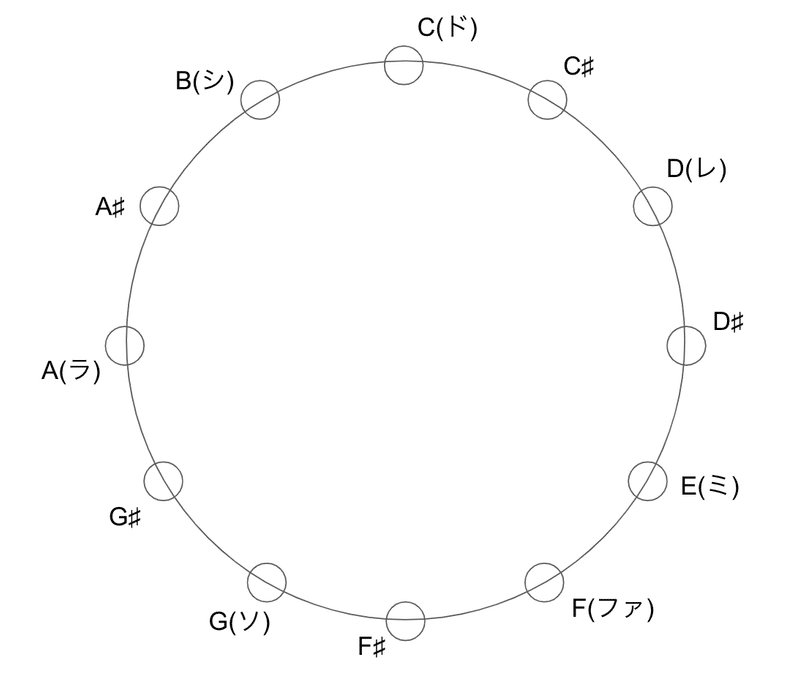
　1オクターブの中には12の音階があるため、ちょうど時計と同じ配置になる。ここで、僕が聴こえた「レ」の音と、12時の位置にある「ド」の音に色をつけてみる。

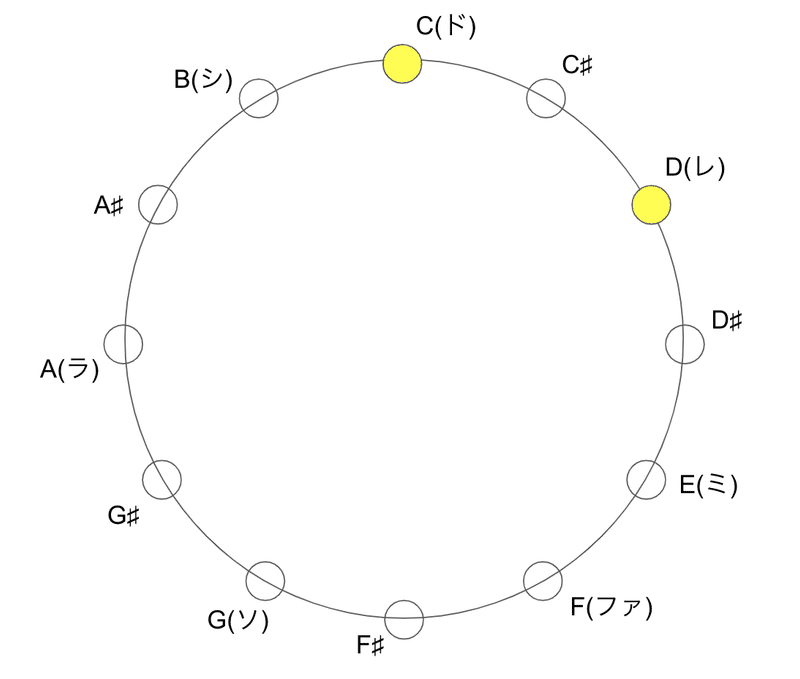
　詳しい説明は省くが、この音は「長2度」つまりオクターブを加えると「長9度」の関係にある。「ド」に対して完全5度の関係にある「ソ」の、さらに完全5度の関係にあるのが「レ」だ。時計回りに「ド → ソ → レ」と回っていく。

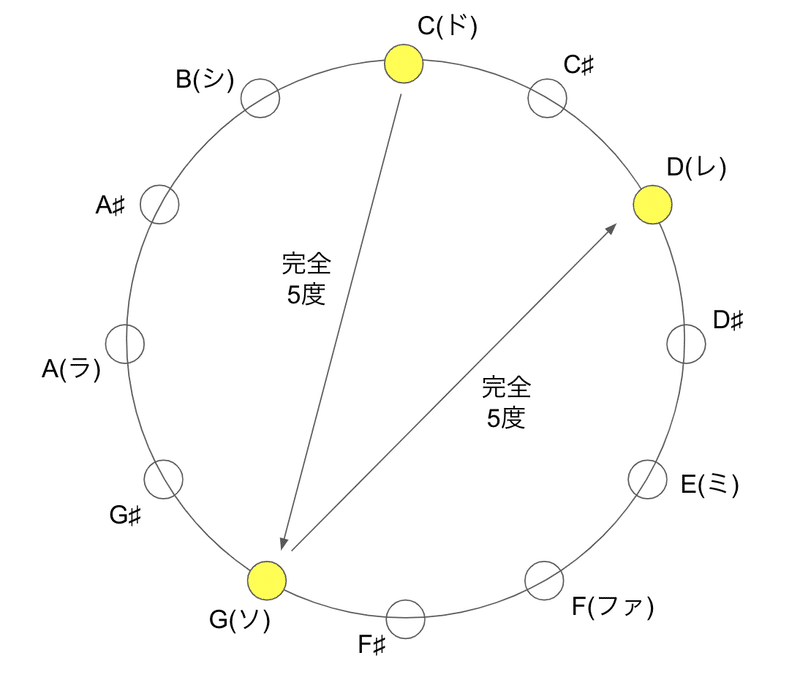
　ギターでは ナインス(9th) と呼ばれる音になり、ナインスを加える(add9)と、透明感を帯びた綺麗な響きになる。これだけ美しい関係にあれば、たしかに響きも美しくなるのは納得だ。

反時計回りに回ってみる

　今度は「ド」から、反時計回りに考えてみる。逆完全5度（とは言わないと思うが）には「ファ」、そしてさらに逆完全5度には「ラ♯（A♯）」が位置している。

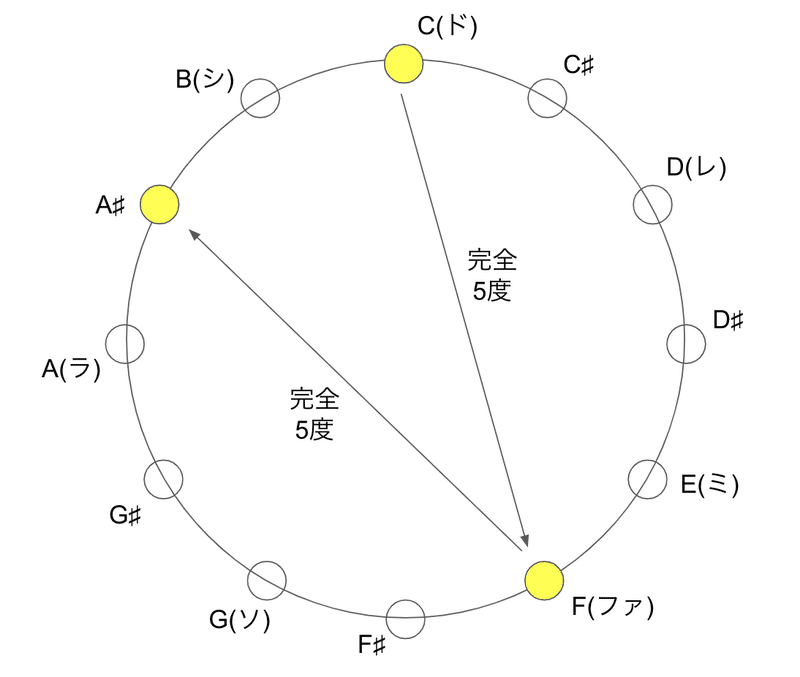
　この音は セブンス(7th) と呼ばれる音で、なんとなく不安・不穏な響きになる。美しいナインスと対局の関係にあるからなのかな、と変に納得する。

　眠れない頭はさらに冴えていく。まだ夜は明けない。

Hzとピタゴラス数

　音の高さは Hz（ヘルツ）で表される。オクターブはHzが倍になると決まっているので、440Hzの ラ（A4）の、オクターブ上のラ（A5）は 880Hzとなる。

　ドレミファソラシドの音階に対してのHzの配列には、純正律と平均律という二つの音律が存在する。同じ音階でも、それぞれの音律によって若干Hzが違うのだが、素人耳にはほとんど違いがない。

　実際に、純正律で 3：4：5 の比率とされている「ド：ファ：ラ」は、平均律でもほぼその比率を守っている。

平均律の音階
ド（C4）　　　261.6 Hz（87.2 × 3）
ファ（F4）　　349.2 Hz（87.3 × 4）
ラ（A4）　　　440.0 Hz（88.0 × 5）

　ちなみに、純正律は「和音が綺麗に鳴るためにHzを調整した音階」、平均律は「数学的にHzが綺麗に配置されるように調整した音階」という感じである。

　そして、3：4：5 と聞くと、ピタゴラス数 を思い出す。

斜辺の長さを c, 他の2辺の長さを a, b とすると、以下が成り立つ。
c^{2}　=　a^{2} + b^{2} （ピタゴラスの定理）
これを満たす整数の組を ピタゴラス数 といい、3, 4, 5 や 5, 12, 13 などが挙げられる。

　これらを踏まえて、先ほどの円形図で「ド・ファ・ラ」をそれぞれ見てみると、たまたま円弧の数が 3：4：5 の関係になっているのだ！

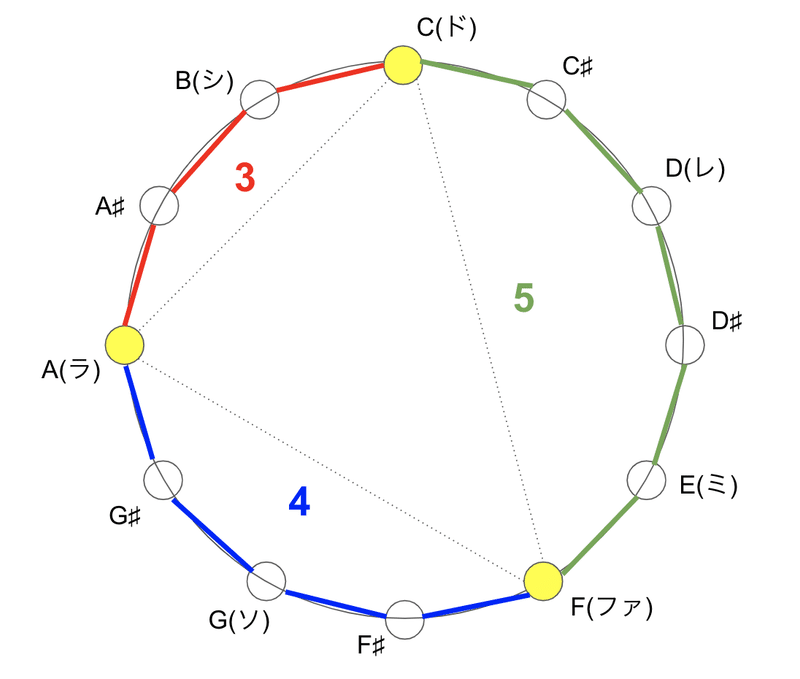
　だからといって、特に何になるわけでもないのだが、なんかすごい発見をしてしまった気がする。「ピタゴラス音律」と呼ばれる音律があるくらいなので、かのピタゴラスも、もしかしたら同じ着想から、ピタゴラスの定理を思いついたのかもしれない（そんなわけはない）。

　眠れない頭は、すでに眠ることを放棄して、さらに思考を深めていく。

数直線上に音階をのせてみる

　先述の通り、オクターブはHzが倍になると決まっているので、aHzの音に対して、2aHz, 4aHz, 8aHzの音も同じ音階になる。

ド（C2）　　　130.8 Hz
ド（C3）　　　261.6 Hz（130.8 × 2）
ド（C4）　　　523.2 Hz（130.8 × 4）
ド（C5）　　　1046.5 Hz（130.8 × 8）

　頭の中で、それぞれの点を数直線上に置いてみる。

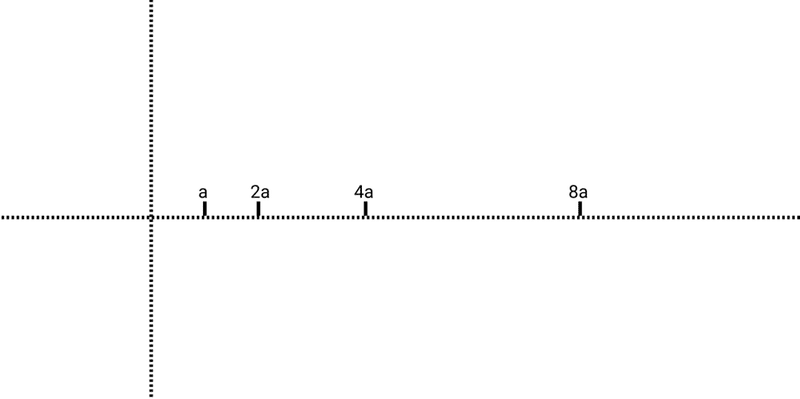
　このx軸はHzを表しており、x軸上にプロットした点（a, 2a, 4a, 8a）は全て同じ音階（先ほどの例だと「ド」）を示している。

　こうなると、xy平面に、Hzと音階の関係を表す曲線を描きたくなってくる。ベットから起き上がり、僕は机に向かう。

xy平面上にHzの曲線を描いてみる

　今度は、原点からの距離をHzとして、xy平面上に曲線を描いてみる。

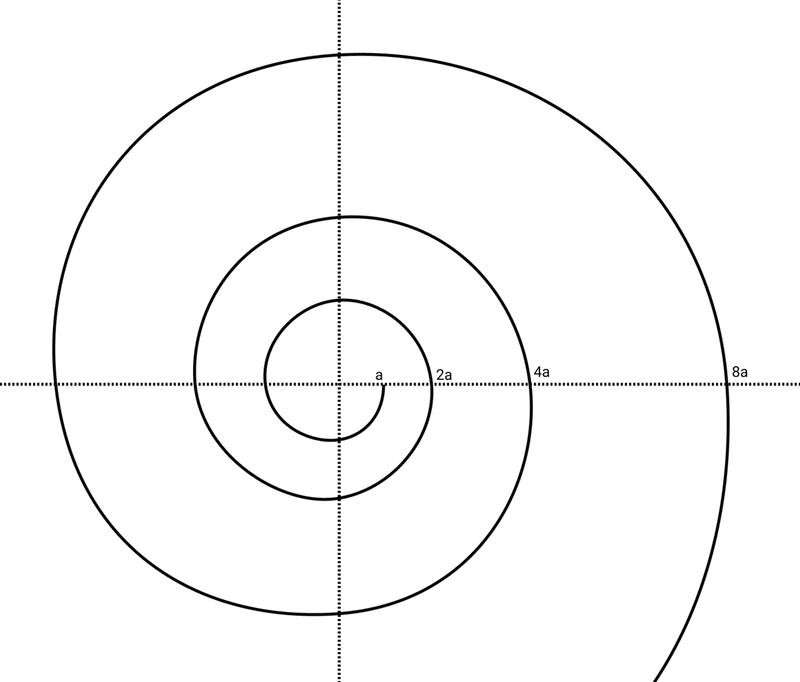
　形はベルヌーイの螺旋のようだ。若干歪んで見えるのは、僕のデザインツールのスキル不足である。そして、任意に引かれる原点からの半直線が曲線と交わる点は、全て同じ音階になる。

　最初の円形図を重ねると、こんな形になる。

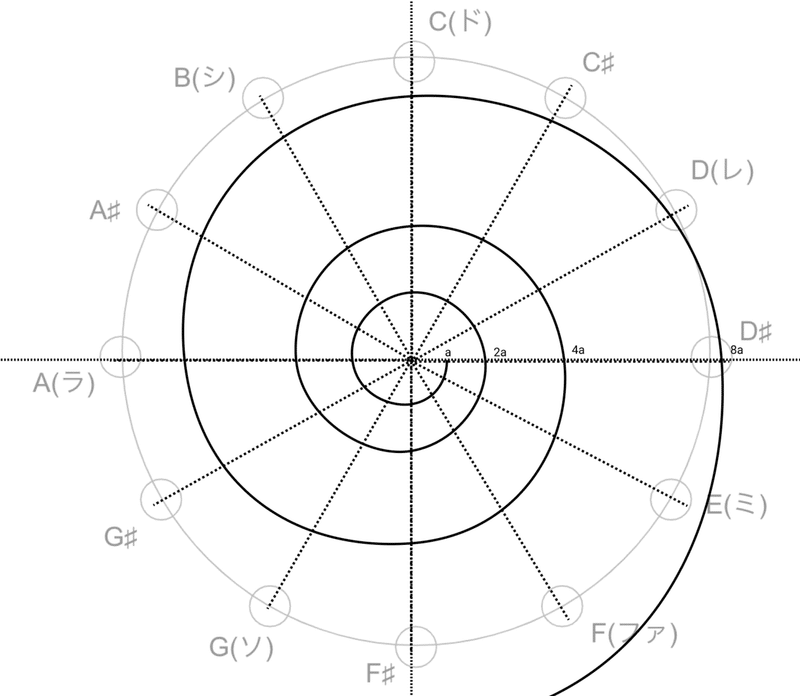
　この曲線と、放射状の半直線が交わる点は、常に同じ音階なのだ。

　どこまで行っても、同じ音階である。
　どこまで行っても、だ。

　なんて美しいのだろう。

平面を立体へ見立てる

　うっとりとこの図を眺めていると、円錐上にぐるぐる巻きつけた紐を、上から見た図のように見えてくる。

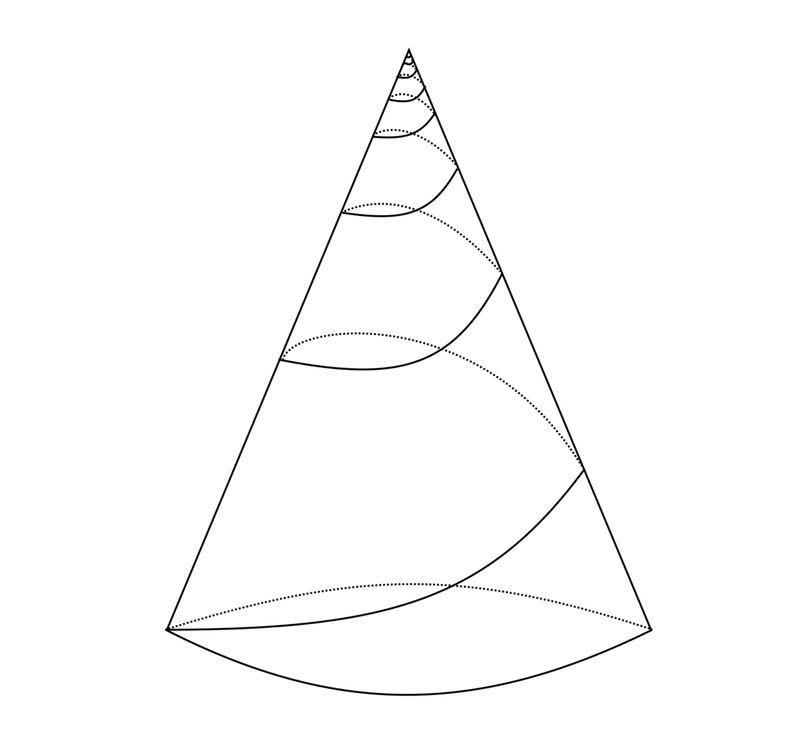
　円錐の表面上に鍵盤を並べてみたら、上下には同じ音階がオクターブ違いで並ぶということだ。これは面白い。音楽と数学が融合した、アート作品の出来上がりである。

　もちろん実際に作成はしていないが、頭の中にはもうすでに作り上げられている。

　そして気づけば、朝になっていた。

----------------------------------------

　懐かしかった。この頃から自分はアートが好きだったのかもしれない。GWも終わったので、仕事モードに切り替えなきゃ。