数学 Project note#1【数学Ⅱ】２つのタワーが同じ高さに（授業想定：２ｈ）

テスト・受験のためだけの教科書”を”教える授業からの脱却を目指し、高校数学のプロジェクト学習を紹介する記事です。不十分な内容があればご指摘いただければ幸いです。

１．２つのタワーが同じ高さに見えるのか？

①まずは、教室で実験（適当な異なる高さの置物で実験）

２．どうして同じ高さに見えるの？（分からければ読み飛ばしてください。）

②教科書の問題を解く（アポロニウスの円の紹介）
２点Ａ、Ｂから距離の比が２：１である点Ｐの軌跡を求める

③ここでDesmos（グラフ計算機）を使用して、生徒と確認
教科書では、式をきれいな形に変形するが、Desmosでは、計算式を入れるだけで円を描いてくれる。（ココがポイント！）

↑のデスモス：https://www.desmos.com/calculator/xmllrr8hyj

④東京タワーとスカイツリーの講義
参考URL：http://club.informatix.co.jp/?p=2763

P1からC、Ｄを見た角度が等しいとき、人は同じ高さにみえる。
ＣＡ：ＤＢ＝333：634
△ＣＡＰ∽△ＤＢＰ より
ＰＡ：ＰＢ＝333：634
となる点Ｐの軌跡を求めればよい。（教科書はＰＡ：ＰＢ＝２：１）

３．実際に計算してみよう

①実践したい２つの塔の高さを調べます。

②２つの塔が地図を用意します。

③Desmosに地図を貼ります。
デスモスURL：https://www.desmos.com/?lang=ja
※左上の「＋ボタン」で「画像を追加」できます。

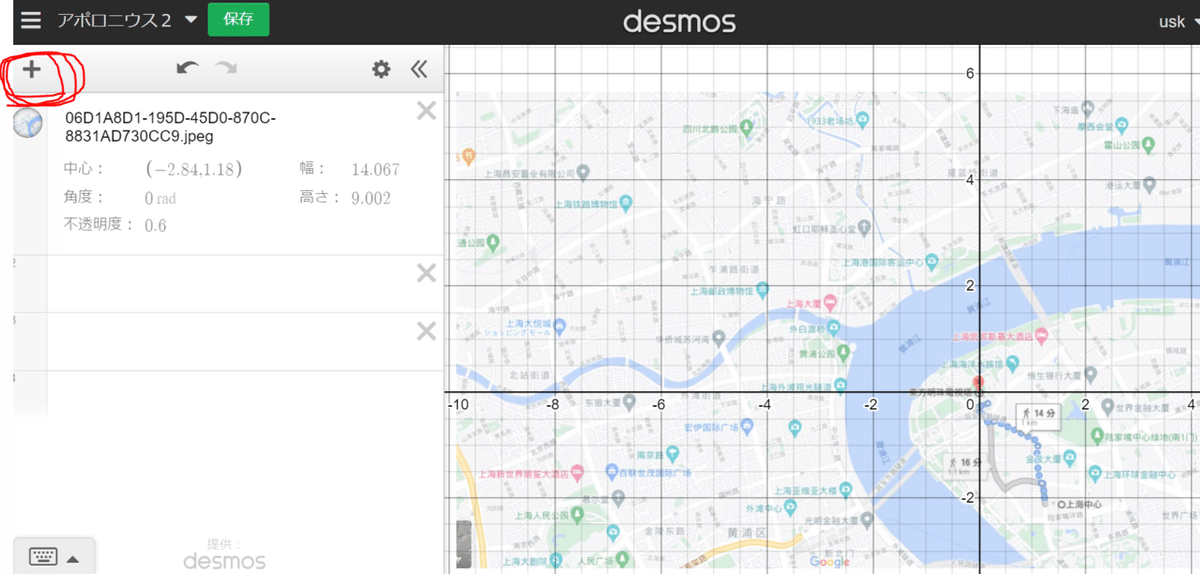
地図を移動して、１つのタワーを原点（0, 0）にすると計算が少し楽になる。

④２つのタワーの地点の座標をとります。
（私の図の場合、A(0,0),  B(1.56, -2.12) ）

⑤教科書の例のように、「ＰＡ：ＰＢ＝470：632」となるアポロニウスの円を描く。
私の図の場合、632^2( x^2 + y^2 ) = 470^2 { (x-1.56)^2 + (y+2.12)^2 }
この図のデスモスです：https://www.desmos.com/calculator/wfrwifgfxx

４．現地に行ってみました！

↓ここに行ってみると…

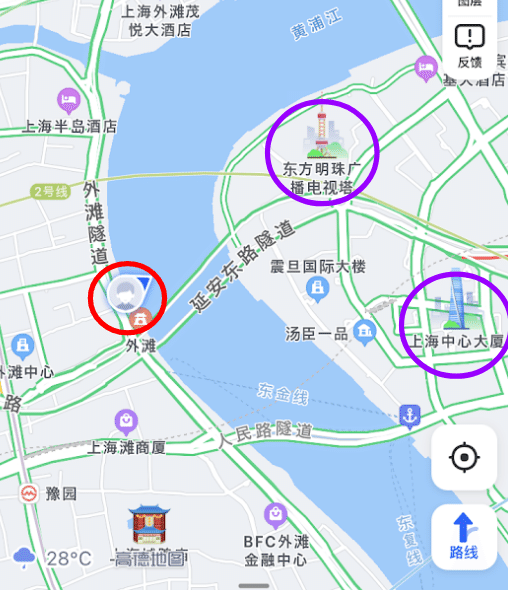
ほぼズレなく、正しい場所を探し当てました！
ちょっと移動すると、こちらに↓

５．感想（授業者）

　①アポロニウスの円の内容（数Ⅱ軌跡と領域）の理解が深まるように感じた。（今回は生徒へアンケートとりませんでした）
　②実際に検証できることで生徒の反応もたいへんよかった。

普段は素通りしていた景色を、教科を学ぶことで、「視点が増える」ことに教科の意義がある。この「教科の補助線を引く」ことを、「教科の見方考え方」なんだと思う。

最後まで読んで頂きありがとうございました