【平方数の規則性の利用】ピタゴラス数の見つけ方

今回は、平方数の規則性の応用として、ピタゴラス数の見つけ方を紹介します。

●ピタゴラス数とは

3つの自然数（正の整数＝小学生範囲で言えば「整数」）A・B・Cについて、A×A＋B×B＝C×C が成り立つ3つの数の組み合わせのこと。

平方数＋平方数＝平方数　が成り立つ3つの数、とも言えます。

例えば有名なもので言えば、3・4・5。
3×3＋4×4＝5×5 （9＋16＝25）が成り立ちます。

中学数学を学べば、三平方の定理（ピタゴラスの定理）として、直角三角形の3辺の長さの関係として扱います。

●ピタゴラス数の見つけ方（奇数から始める）

まず、奇数から始める方法です。

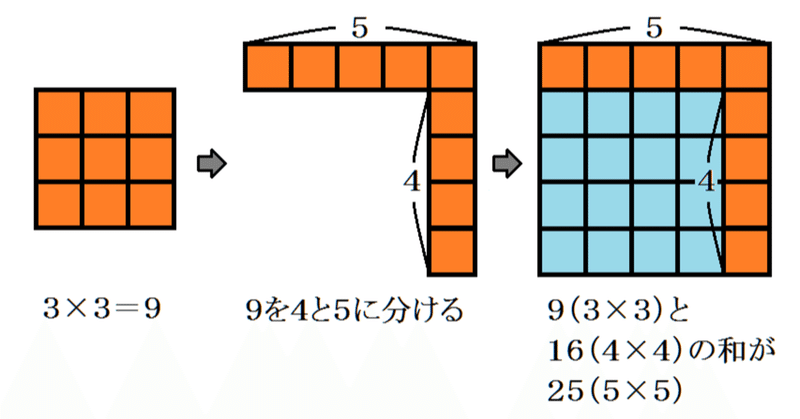
① 3以上の奇数を決め、その平方数を求める。
例：3の場合、3×3＝9

② ①で求めた平方数を、差が1になるよう2数に分ける。
例：9を4と5に分ける

③ ①で決めた奇数と、②で分けた2数の3つがピタゴラス数
例：3・4・5

3×3＋4×4＝5×5 （9＋16＝25）

３・４・５の場合を例に、図にすると以下のような形です。

これは、以下の記事の考え方を利用したものです。

他の数でも実際に試してみます。

●5から始める場合

① 3以上の奇数を決め、その平方数を求める。
例：5の場合、5×5＝25

② ①で求めた平方数を、差が1になるよう2数に分ける。
例：25を12と13に分ける

③ ①で決めた奇数と、②で分けた2数の3つがピタゴラス数
例：5・12・13

5×5＋12×12＝13×13（25＋144＝169）

●7から始める場合

① 3以上の奇数を決め、その平方数を求める。
例：7の場合、7×7＝49

② ①で求めた平方数を、差が1になるよう2数に分ける。
例：49を24と25に分ける

③ ①で決めた奇数と、②で分けた2数の3つがピタゴラス数
例：7・24・25

7×7＋24×24＝25×25（49＋576＝625）

といった具合に、最初に選ぶ数が奇数の場合はこの方法で無限にピタゴラス数が見つかります。

●ピタゴラス数の見つけ方（偶数から始める）

続いて、偶数から始める方法です。

① 4以上の偶数を決め、その平方数を求めて2で割る。
例：4の場合、4×4＝16
　　16÷2＝8

② ①で求めた「平方数÷2」の商を、差が2になるよう2数に分ける。
例：8を3と5に分ける

③ ①で決めた偶数と、②で分けた2数の3つがピタゴラス数
例：3・4・5

3×3＋4×4＝5×5 （9＋16＝25）

上の例を図にすると以下のような形です。

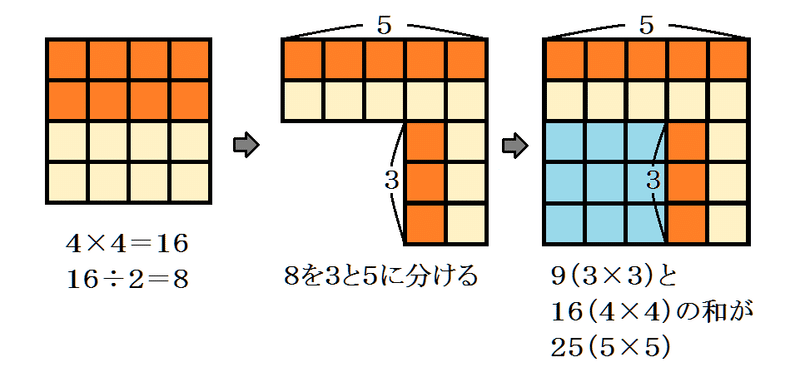
奇数のときと比べて少しわかりにくくなっていますが、図のオレンジと薄黄の部分が4×4＝16で、水色の部分が3×3＝9です。

他の数でも実際に試してみます。

●6から始める場合

① 4以上の偶数を決め、その平方数を求めて2で割る。
例：6の場合、6×6＝36
　　36÷2＝18

② ①で求めた「平方数÷2」の商を、差が2になるよう2数に分ける。
例：18を8と10に分ける

③ ①で決めた偶数と、②で分けた2数の3つがピタゴラス数
例：6・8・10

6×6＋8×8＝10×10 （36＋64＝100）

●8から始める場合

① 4以上の偶数を決め、その平方数を求めて2で割る。
例：8の場合、8×8＝64
　　64÷2＝32

② ①で求めた「平方数÷2」の商を、差が2になるよう2数に分ける。
例：32を15と17に分ける

③ ①で決めた偶数と、②で分けた2数の3つがピタゴラス数
例：8・15・17

8×8＋15×15＝17×17 （64＋225＝289）

偶数スタートの場合は、3・4・5のそれぞれを2倍しただけの6・8・10のように、既に見つかった組み合わせを2倍した組み合わせも見つかってしまいます。

中学受験では、三平方の定理を必要とする問題は出題されませんが、平方数の規則性の応用として紹介してみました。
数の性質というものは、奥が深いものです。