ペンローズのグラフ記法によるベクトル解析の公式の表現

pdf版はこちらから。動画解説は以下から。

電磁気学以来、ベクトル解析の公式は決して暗記できるようなものではないと私が感じていたように、ベクトルの公式を覚えられない物理学徒は多いことと思います。「レビチビタ記号の縮約公式がわかれば覚えなくていい」とか言われますけど、電磁気の教科書読んでたらどう考えたっていちいちレビチビタ使って導出するのも億劫になりますよね。

しかし、ペンローズのグラフ記法 (Penrose graphical notation; tensor diagram notation) という強力なツールに出会ったことで、これらのベクトル解析の公式を暗記することなく、暗算によって求められるようになりました。

前提知識

この記事では以下を前提知識とします。

• スカラーとベクトルの区別

• 内積と外積の定義

• grad, div, rot, ラプラシアン

• アインシュタインの縮約記法

• クロネッカーのデルタ

• レビチビタ記号とその縮約公式

• 外積のレビチビタ記号による表示

基本的に添字を使う場合はアインシュタインの縮約記法に従って表します。また、本記事では共変・反変の区別をしません。

基本事項

スカラーとベクトルは「脚」の有無で判別します。

脚が1本あればベクトル、なければスカラー

文字式同様、図式を並べるだけでスカラー倍を表すことができます。

ベクトルの脚と脚をつなぎ合わせることで内積を取ることができます。

クロネッカーのデルタの脚が繋ぎ合わさって内積に

アインシュタインの縮約を使ってクロネッカーのデルタを明示的に表すのであれば、$${\bm{u}\cdot\bm{v}=u_i\delta_{i,j}v_j}$$のようになりますね。

反対称性（外積）

横の太線は反対称性を表します。つまり脚の位置を奇置換すると符号が反転します。これを使ってレビチビタ記号$${\epsilon_{ijk}}$$は下のように表せます。

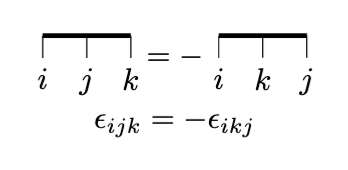
これに基づいて外積はこのように表すことができます。

ベクトルを表す脚は、今のところ向きを問わない

一番左に先が空いている脚が伸びているのでベクトルであることがわかります。アインシュタインの縮約記法でも$${(\bm{u}\times\bm{v})_i=\epsilon_{ijk}u_jv_k}$$となって添字$${i}$$が残っていますね。

公式１：ベクトルの内積と外積にまつわる公式

レビチビタ記号の縮約公式

$$
\epsilon_{ijm}\epsilon_{klm}=\delta_{ik}\delta_{jl}-\delta_{il}\delta_{jk}
$$

これだけは覚えてください。他は何も要りませんから。

スカラー三重積

$$
\begin{array}{} \bm{A}\cdot (\bm{B} \times \bm{C}) = \bm{B}\cdot(\bm{C}\times \bm{A}) = \bm{C}\cdot(\bm{A} \times \bm{B})\\= –\bm{A}\cdot(\bm{C} \times \bm{B}) = –\bm{B}\cdot(\bm{A} \times \bm{C}) = –\bm{C}\cdot(\bm{B} \times \bm{A}) \end{array}
$$

偶置換及び奇置換をして求まります。

A→B→C→Aの順序を崩さなければ値は同じですね。奇置換なら符号が反転します。

ベクトル三重積

$$
\bm{A}\times(\bm{B}\times \bm{C})=\bm{B}(\bm{A}\cdot \bm{C})-\bm{C}(\bm{A}\cdot \bm{B})
$$

縮約公式から求まります。その際、最初は図の１行目のように偶置換することで形を整えてあげるのがいいでしょう。

ベクトル四重積

$$
\begin{array}{rcl} (\bm{A} \times \bm{B})\cdot(\bm{C} \times \bm{D}) &=& \det \left(\begin{array}{}\bm{A}\cdot \bm{C}& \bm{A}\cdot \bm{D}\\ \bm{B}\cdot \bm{C}& \bm{B}\cdot \bm{D}\end{array}\right)\\ &=&(\bm{A}\cdot \bm{C})(\bm{B}\cdot \bm{D})-(\bm{A}\cdot \bm{D})(\bm{B}\cdot \bm{C})\end{array}
$$

レビチビタ記号の縮約公式から求められます。

あからさまに「行列式だ」とわかる形ではありませんが、行列式を展開すればピッタリ一致することがわかります。レビチビタ記号の縮約を行列式によって表す流儀があることを考えると自明。

スカラー・ベクトルの共変微分作用素

ペンローズのグラフ記法で$${\nabla}$$（ナブラ）を表すには、微分する対象を丸で囲い、丸から脚を伸ばします。

$${\nabla}$$を用いた記法と全く同様に grad, div, rot, $${\Delta}$$（ラプラシアン）を図形的に表すことができます。

勾配 grad

$$
\mathrm{grad}\;f=\nabla f
$$

スカラーを丸で囲って丸から脚を伸ばします。

発散 div

$$
\mathrm{div}\; \bm{v} = \nabla\cdot \bm{v}
$$

微分対象のベクトルの脚と丸から伸ばした脚を繋げます。

ベクトルにしか作用しないことが視覚的に自明

回転 rot

$$
\mathrm{rot}\:\bm{v} = \nabla \times \bm{v}
$$

外積同様に表します。このとき、$${∇}$$ に相当する丸から伸びる脚の根本は必ず微分対象のすぐ左に繋げます。

「微分対象のすぐ左」のルールに従わないと、後述の div (u×v) などに響く

ラプラシアン △

$$
\nabla^2=\nabla\cdot\nabla=\triangle
$$

図でも$${\nabla}$$と$${\nabla}$$の内積で表します。微分対象はスカラーでもベクトルでも構いません。

微分対象がスカラーでもベクトルでも表記に齟齬を生じない

上側の図から一眼で $${\mathrm{div\:grad}\:f = \triangle f}$$ がわかります。

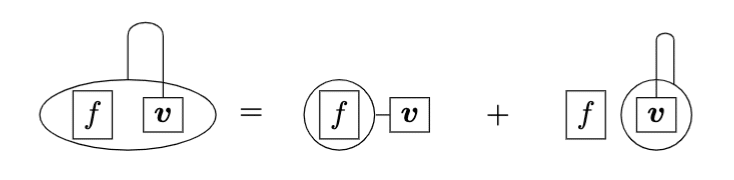
積の微分（ライプニッツ・ルール）

微分作用素はライプニッツ・ルールに従って展開することができます。

$$
\nabla (AB) = (\nabla A)B + A(\nabla B)
$$

この図でのA, Bはベクトルでもスカラーでも可
積の形状はAとBがそれぞれ何かによる

微分順序交換

また $${C^2}$$ 級関数 (2階微分が連続な関数) に対しては微分順序を入れ替えても問題ありません。すなわち丸の内外を入れ替えることができます。

ここでは問題にならないが、内側の丸を先に演算する

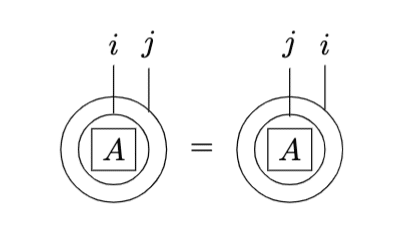
なお、以降の公式で丸が２つ出てくるものは、ペンローズの記法を使う使わないによらず、基本的に $${C^2}$$ 級を仮定しています。

公式２：ベクトルの微分作用素にまつわる公式

以下の公式は、下の5種類の変形のみを用いて、半ば暗算でペンローズのグラフ記法から導出することができます。

• 積の微分（ライプニッツ・ルール）

• レビチビタ記号の縮約公式

• 反対称性（奇置換）

• 微分順序交換

• 偶置換

レビチビタ記号を用いた添字記法による公式の証明と全く同じ流れで導出されます。

rot grad f = ∇ × ∇ f = 0

$$
\mathrm{rot\:grad}\:f=\nabla\times\nabla f=0
$$

微分順序の交換と反対称性（奇置換）を使います。

1つ目の等号が微分順序交換、2つ目が奇置換

左辺と右辺を比較すると $${A = – A}$$ の形になっているので、両辺ともにベクトル $${\bm{0}}$$ であることがわかります。

div rot v = ∇・(∇ × v) = 0

$$
\mathrm{div\:rot}\:\bm{v}=\nabla\cdot(\nabla\times\bm{v})={0}
$$

上と同様に微分順序交換と反対称性を使います。

１行目が微分の順序交換、２行目が左辺の奇置換

右辺を比べると $${A = – A}$$ の形になっていますから、値はともに $${0}$$ であることがわかります。

div grad f = △ f

$$
\mathrm{div\:grad}\:f=\triangle f
$$

先ほども確認しましたが、公式として再掲します。

grad (fg) = (grad f) g + f (grad g)
∇ (fg) = (∇ f) g + f (∇ g) = 0

$$
\begin{array}{rcl} \mathrm{grad}\:(fg)&=&(\mathrm{grad}\:f)g+f(\mathrm{grad}\:g)\\ \nabla(fg)&=&(\nabla f)g+f(\nabla g)\end{array}
$$

積の微分で表せます。

div (f v) = (grad f)・v + f (div v)
∇・(f v) = (∇ f)・v + f (∇・v)

$$
\begin{array}{rcl} \mathrm{div}(f\bm{v})&=&(\mathrm{grad}\:f)\cdot\bm{v}+f\:\mathrm{div}\:\bm{v}\\ \nabla\cdot (f\bm{v})&=&(\nabla f)\cdot\bm{v}+f\nabla\cdot\bm{v}\end{array}
$$

これも積の微分です。

div (u × v) = (rot u)・v - u・(rot v)
∇・(u × v) = (∇ × u)・v - u・(∇ × v)

$$
\begin{array}{rcl}\mathrm{div}\:(\bm{u} \times \bm{v}) &=& (\mathrm{rot}\:\bm{u})\cdot \bm{v} - \bm{u}\cdot(\mathrm{rot}\: \bm{v})\\\nabla\cdot(\bm{u}\times\bm{v}) &=& (\nabla\times\bm{u})\cdot\bm{v} - \bm{u}\cdot(\nabla \times \bm{v})\end{array}
$$

積の微分で微分作用素をバラした後、「丸から伸びる脚の根本は必ず微分対象のすぐ左」の原則に従うように、反対称性を使って第2項を変形します。

2行目第2項は1行目右辺の奇置換

rot (f v) = (grad f) × v + f (rot v)
∇ × (f v) = (∇ f) × v + f (∇ × v)

$$
\begin{array}{rcl} \mathrm{rot} (f \bm{v}) &=& (\mathrm{grad} \: f) \times \bm{v} + f \: \mathrm{rot}\: \bm{v} \\ \nabla \times(f \bm{v}) &=& (\nabla f) \times \bm{v} + f (\nabla \times \bm{v})\end{array}
$$

積の微分です。

微分の内外さえ守っていればfの位置はどこでも構わない

見やすくなるように右辺第2項は、スカラー$${f}$$を $${\mathrm{rot}}$$ の前に持ってきています。

rot (u × v) = (v・grad) u + u div v – v div u – (u・grad) v
∇ × (u × v) = (v・∇) u + u ∇・v – v ∇・u – (u・∇) v

$$
\begin{array}{rcl} \mathrm{rot}\: (\bm{u} \times \bm{v}) &=& (\bm{v}\cdot \mathrm{grad}) \bm{u} + \bm{u}\:\mathrm{div}\:\bm{v} - \bm{v}\:\mathrm{div}\:\bm{u} - (\bm{u}\cdot \mathrm{grad}) \bm{v} \\ \nabla\times (\bm{u}\times \bm{v}) &=& (\bm{v}\cdot\nabla) \bm{u} + \bm{u}\:\nabla\cdot\bm{v} - \bm{v}\:\nabla\cdot\bm{u}- (\bm{u}\cdot\nabla) \bm{v} \end{array}
$$

レビチビタの縮約公式と積の微分で示せます。

1行目から順に、レビチビタ記号の縮約、ライプニッツ・ルール

1行目の変形は縮約公式を見やすくするために u × v のレビチビタ記号で偶置換しています。

rot (rot v) = grad (div v) - △ v
∇ × (∇ × v) = ∇ (∇・v) - ∇^2 v

$$
\begin{array}{rcl} \mathrm{rot} (\mathrm{rot} \bm{v}) &=& \mathrm{grad} (\mathrm{div} \bm{v}) - \Delta \bm{v} \\ \nabla\times (\nabla\times\bm{v}) &=& \nabla (\nabla\cdot\bm{v}) - \nabla^2 \bm{v}\end{array}
$$

レビチビタの縮約公式を使ってから微分順序の交換を行います。

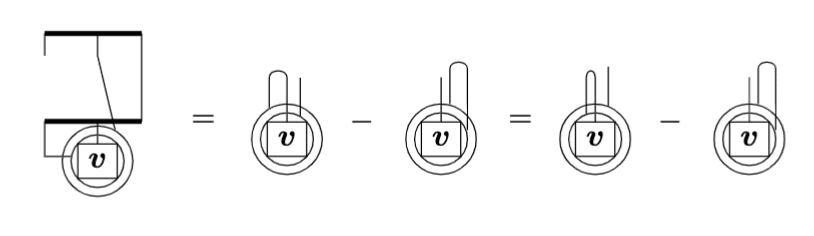
微分順序の交換をしているのは、2行目の第1項に相当する演算が存在しないためです。

grad (u・v) = v × (rot u) + (v ・ ∇) u + u × (rot v) + (u・∇) v
∇ (u・v) = v × (∇ × u) + (v・∇) u + u × (∇ × v) + (u・∇) v 
u)

$$
\begin{array}{rcl} \mathrm{grad}\: (\bm{u}\cdot\bm{v}) &=& \bm{v}\times (\mathrm{rot}\: \bm{u}) + (\bm{v}\cdot \mathrm{grad}) \bm{u} + \bm{u} \times (\mathrm{rot} \:\bm{v}) + (\bm{u}\cdot \mathrm{grad}) \bm{v}\\ \nabla (\bm{u}\cdot\bm{v}) &=& \bm{v} \times (\nabla \times \bm{u}) + (\bm{v}\cdot\nabla) \bm{u} + \bm{u} \times (\nabla \times \bm{v}) + (\bm{u}\cdot\nabla) \bm{v}\end{array}
$$

こいつに関しては一筋縄ではいきません。まずは左辺を積の微分で展開します。

右辺に相当する演算記号は存在しない

右辺に相当する演算記号がないので、各項をレビチビタの縮約公式によって展開された後の形と考えて、次の式を持ち出します。

右辺第1項が先ほどの式の右辺第1項。

これを移項して元の式に代入します。第2項についても同様に考えると、答えが得られます。

△ (fg) = f (△ g) + 2 (grad f)・(grad g) + (△ f) g
∇^2 (fg) = f (∇^2 g) + 2 (∇ f)・(∇ g) + (∇^2 f) g

$$
\begin{array}{rcl}\triangle(fg)&=&f(\triangle g)+2(\mathrm{grad}\:f)\cdot(\mathrm{grad}\:g)+(\triangle f)g\\ \nabla^2(fg)&=&f(\nabla^2 g)+2(\nabla f)\cdot(\nabla g)+(\nabla^2f)g\end{array}
$$

2回にわたって積の微分を展開すれば得られます。

公式3：位置ベクトルを含む微分公式

特に位置のベクトル$${\bm{r}}$$と微分演算子$${\nabla}$$を含む計算では次の縮約が可能です。

$$
\dfrac{∂}{∂r_i}r_j\bm{e}_j=\delta_{ij}\bm{e}_j
$$

これをペンローズのグラフ記法で描くと、$${∇}$$を表す円と位置ベクトルの四角が消えて線が繋がるように表せます。

∇を表す円と位置ベクトルを表す四角が消えて線が繋がる

ここではギリギリ「公式」と呼べる程度のものを拾っていきます。

div r = δ_{ii} = 3
∇・r = δ_{ii} = 3

$$
\begin{array}{rcl}\mathrm{div}\:\bm{r}&=&\delta_{ii}&=&3\\\nabla\cdot\bm{r}&=&\delta_{ii}&=&3\end{array}
$$

右辺の輪っかはクロネッカーのデルタの両側がつながった状態と捉えて$${\delta_{ii}}$$となります。$${3}$$は次元数です。$${4}$$次元になれば$${\mathrm{div}\:\bm{r}=4}$$に、$${n}$$次元になれば$${\mathrm{div}\:\bm{r}=n}$$になります。

rot r = 0
∇ × r = 0

$$
\begin{array}{rcl}\mathrm{rot}\:\bm{r}&=&0\\\nabla\times\bm{r}&=&0\end{array}
$$

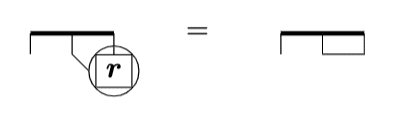
右辺は$${\epsilon_{ijk}\delta_{jk}}$$を表しますので、$${\epsilon_{ijj}=0}$$となります。

テンソルへの拡張

ペンローズのグラフ記法は元々テンソルのために開発されたもので、高度な計算ではより力を発揮してくれます。

レビチビタ記号を使うと行列式や余因子展開が直観的に表示できます。

今回大活躍したレビチビタ記号をテンソルに拡張したのがこちら。

テンソル解析の中でも微分とレビチビタ記号をふんだんに使う微分形式もお手のものになります。

参考文献

• Roger Penrose "Applications of negative dimensional tensors," in Combinatorial Mathematics and its Applications, Academic Press (1971)

• Roger Penrose, Wolfgang Rindler "Spinors and Space-Time Volume 1: Two-Spinor Calculus and Relativistic Fields", Cambridge University Press (1984)

• 「ペンローズのグラフ記法」Wikipedia