主成分分析のイメージを掴んで実装してみる(2/2)
機械学習の前処理である次元削減について書いています。
次元削減には大きく特微量選択と特微量抽出があります。前々回はその全体像と特微量選択(逐次特微量選択)について書きました。前回は、特微量抽出のひとつである主成分分析の概要について書いてみました。
今回は、主成分分析の原理をゆるふわに見た上で、逐次特微量選択との比較をしてみたいと思います。
なお、この記事は「カーネル多変量解析」を読むシリーズの一部です。
前回のふりかえり
主成分分析は「データのバラツキが大きい軸を見つけて射影すればその軸で説明できることが多いので、そういう軸を順次決めることで、本来の次元数より少ない次元に射影できる=次元削減できる」という考え方でした。
そして、そのバラツキが大きい軸(主成分)とは「サンプルデータの共分散行列の固有ベクトルのうち固有値が最大のものである」という言葉の意味を確認し、確かにそうなってそうなことを確認しました。
ではどうしてその選び方で主成分が選べるのでしょうか?
なぜ固有ベクトルが主成分になるのか?
まず、主成分を定義してみます。データのバラツキが大きい軸ということなのですが、それって感覚的にいうと「全てのデータの真ん中を通る軸」です。めちゃ感覚的。
もう少し真面目に定義すると、「ある直線があったとき、各データとの距離の二乗和が最小なら、その直線は主成分」と言えそうです。
図で考えてみるとこんな感じ。

この図はn次元空間で、黒線が主成分です。直線なので、n次元だろうがこんな感じに書けます。また、標準化により全てのデータの平均値が0なので、この線は原点を通ります。計算しやすいように、大きさ1のベクトル$${w}$$を主成分に沿って0から生やします(赤)。
さて、主成分(黒線)と点$${x^{(i)}}$$との距離が「データとの距離」と言えます。n次元でも三平方の定理は成り立つので、「$${x^{(i)}}$$との距離の二乗」は、「$${x^{(i)}}$$の長さの二乗」から「$${x^{(i)}}$$を$${w}$$に射影した長さの二乗」と言えます。
式でいうと、$${|x^{(i)}|^2-|wx^{(i)}|^2}$$。これの和を最小にするってことは、下記を最小にするってことです。
$${\sum_i(|x^{(i)}|^2-|wx^{(i)}|^2)}$$=$${\sum_i|x^{(i)}|^2-\sum_i|wx^{(i)}|^2}$$
前半の$${\sum_i|x^{(i)}|^2}$$は固定値なので、$${\sum_i|wx^{(i)}|^2}$$を最大にするような$${w}$$が主成分の単位ベクトルになります。
そこで$${|wx^{(i)}|^2}$$をよくみてみます。$${w=(w_1,w_2,…,w_n)}$$とし、$${x^{(i)}=(x^{(i)}_1,x^{(i)}_2,…,x^{(i)}_n)}$$とすると、
$${|wx^{(i)}|^2}$$
=$${(w_1x^{(i)}_1+w_2x^{(i)}_2+…+w_nx^{(i)}_n)^2}$$
=$${(w_1x^{(i)}_1+w_2x^{(i)}_2+…+w_nx^{(i)}_n)(x^{(i)}_1w_1+x^{(i)}_2w_2+…+x^{(i)}_nw_n)}$$
=$${(w^Tx^{(i)})(x^{(i)T}w)}$$
=$${w^Tx^{(i)}x^{(i)T}w}$$
計算ステップをとても細かく書いているのでやや長くみえますが、やっていることは単純です。
さて、$${\sum_i|wx^{(i)}|^2}$$を最大にするような$${w}$$が主成分の単位ベクトルなのでした。さっきの計算で放っておいた$${\sum_i}$$を戻してやると、
$${\sum_i|wx^{(i)}|^2}$$
=$${\sum_iw^Tx^{(i)}x^{(i)T}w}$$
=$${w^T\sum_i(x^{(i)}x^{(i)T})w}$$
=$${w^T(xの共分散行列)w}$$
ということで共分散行列が出てきました。共分散行列が$${\sum_i(x^{(i)}x^{(i)T})}$$であることはイメージつくと思いますが、前回簡単に示してもいます。
あとはこれを最大にすればいいのですから、ラグランジュの未定乗数法(いかつい名前ですが、やってることは単純。こちらなど参考)を使って偏微分すると、
$${(xの共分散行列)w = \lambda w}$$
ということで、主成分の単位ベクトル$${w}$$は$${x}$$の共分散行列の固有ベクトル(のひとつ)ということが示せました。
最後になぜ複数ある$${\lambda}$$の中で$${\lambda}$$最大のときに主成分になるか、です。これは上の式を変形したらすぐで、$${(xの共分散行列)w = \lambda w}$$に左から$${w^T}$$をかけると、$${w^T(xの共分散行列)w = w^T\lambda w}$$。$${\lambda}$$はスカラーかつ、$${w}$$は単位ベクトルなので、$${w^T(xの共分散行列)w = \lambda}$$。左辺を最大にしたかったのだから、$${\lambda}$$最大のときが求める主成分です。
式変形だけだとゆるふわじゃないので、二次元で単位ベクトル$${w}$$をぐるぐる回しながら、$${|wx^{(i)}|^2}$$=$${w^T(xの共分散行列)w}$$を描画してみます。
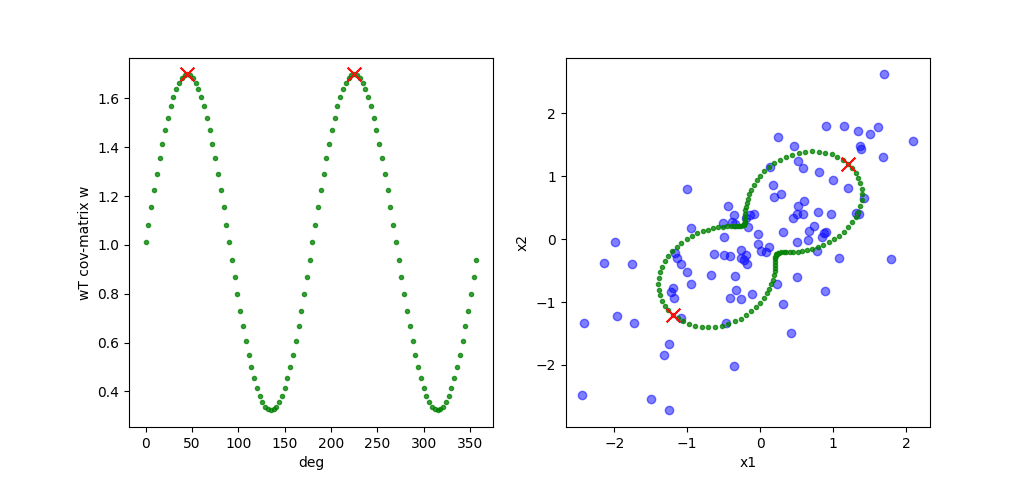
左の図は$${w}$$の角度を変えながら$${|wx^{(i)}|^2}$$=$${w^T(xの共分散行列)w}$$を計算したものです。横軸は360度にしてます。赤いバツが最大のときですね(逆に、一番下の0.4あたりはもう一つの固有ベクトルです)。
右の図は、それを元データの上にマッピングしたものです。最大のバラツキと思しき向きにバツが来ています。
実装してみる
ということで理論がなんとなくわかったので実装です。前々回のwineデータを処理してみます。
前回同様データを訓練データとテストデータにわけます。
import wine
from sklearn.model_selection import train_test_split
X, y = wine.data()
X_train, X_test, y_train, y_test \
= train_test_split(X, y, stratify=y, test_size=0.3, random_state=1)標準化します。xの訓練データをもとに、訓練データとテストデータを標準化しています。
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)主成分となるベクトルを取得します。二つ目も取得しています。
import numpy as np
cov = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov)
eigen_vals = np.abs(eigen_vals)
sorted_indices = np.argsort(-eigen_vals)#降順にするために-をつけた
first_vec = eigen_vecs[:,sorted_indices[0]]
second_vec = eigen_vecs[:,sorted_indices[1]]取得できたベクトルはこんな感じ。
[ 0.12221148 -0.24391049 0.00369454 -0.249647 0.13011026 0.39099441
0.41649235 -0.31569983 0.2982478 -0.07304049 0.31641846 0.37253046
0.29514562]
[-0.49927666 -0.15419073 -0.25170137 0.12269609 -0.31420427 -0.05595656
0.02637354 -0.07362469 0.01094724 -0.53961007 0.21061646 0.23649287
-0.38598117]この二つのベクトルをくっつけて変換用の行列を作り、標準化したデータに右からかければ、二次元に圧縮できます(固有値の大きい順にk個とればk次元に圧縮されます)。
conv_matrix = np.hstack((first_vec[:, np.newaxis], second_vec[:, np.newaxis]))
X_train_std_conv = X_train_std.dot(conv_matrix)
X_test_std_conv = X_test_std.dot(conv_matrix)試しにX_train_stdのデータを三つだけ取り出してきて、変換前と後をみると、13次元のデータが2次元に圧縮されています。
[[ 0.1937094 2.37977151 -0.20420766 0.7516873 -0.37917036 -0.90757407
-1.37745448 2.00281197 -0.08550407 1.17204713 -1.5782345 -1.64200771
-0.08460637]
[ 0.92207682 -0.70975882 1.25077192 -0.03264879 2.61733743 1.06316198
0.71546023 1.10044614 -0.436656 0.11881796 1.40544599 0.55879351
1.47960155]
[ 0.88504119 -0.73508284 1.25077192 0.90855452 0.2354979 1.14459736
1.22133061 -0.62225227 1.37177644 0.24520546 1.13002933 0.1389038
1.63295526]]
[[-3.60252556 -1.65534122]
[ 1.95604795 -1.82561351]
[ 2.53103837 -1.06863621]]この二軸でマッピングしてみましょう。x軸が1つめの主成分、y軸が2つめの主成分で、3種類のクラスに色分けしています。
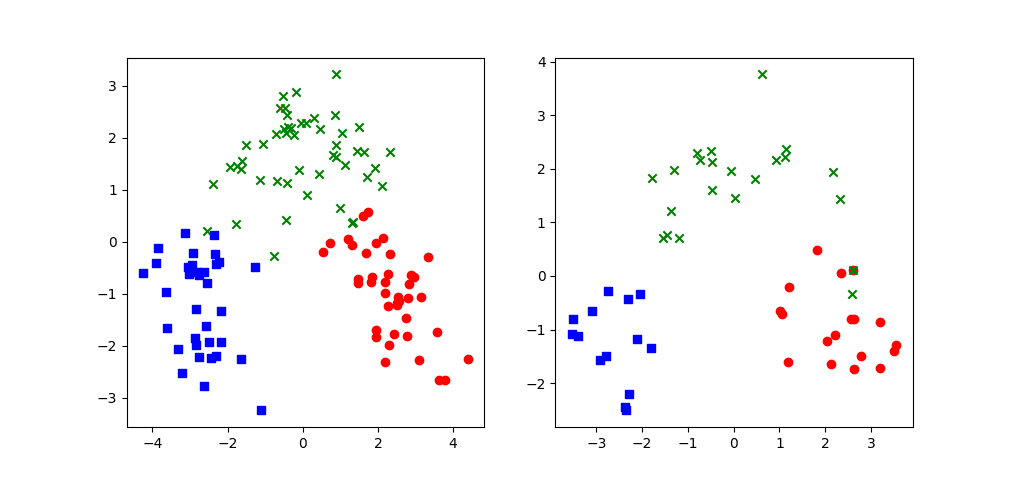
前回の逐次特微量選択のトップ2でマッピングしたときはこうでした。主成分分析の方が綺麗に分かれているように見えます。念のため、これらの処理はあくまで前処理で、予測モデルはこの後別途作ることは思い出しておきましょう。

最後にこれを行列式で表すと(標準化されている前提)、
$${\begin{pmatrix}x^{(1)}_1&x^{(1)}_2&x^{(1)}_3&…&x^{(1)}_{13}\\x^{(2)}_1&x^{(2)}_2&x^{(2)}_3&…&x^{(2)}_{13}\\…&…&…&…&…\\x^{(n)}_1&x^{(n)}_2&x^{(n)}_3&…&x^{(n)}_{13}\end{pmatrix}\begin{pmatrix}0.122&-0.499\\-0.244&-0.154\\0.004&-0.252\\-0.250&0.123\\0.130&-0.314\\0.391&-0.056\\0.416&0.026\\-0.316&-0.074\\0.298&0.011\\-0.073&-0.540\\0.316&0.211\\0.373&0.236\\0.295&-0.386\end{pmatrix}=\begin{pmatrix}x^{(1)}_a&x^{(1)}_b\\x^{(2)}_a&x^{(2)}_b\\…&…\\x^{(n)}_a&x^{(n)}_b\end{pmatrix}}$$
下の特微量抽出に比べるとかなり複雑な変換です。
$${\begin{pmatrix}x^{(1)}_1&x^{(1)}_2&x^{(1)}_3&…&x^{(1)}_{13}\\x^{(2)}_1&x^{(2)}_2&x^{(2)}_3&…&x^{(2)}_{13}\\…&…&…&…&…\\x^{(n)}_1&x^{(n)}_2&x^{(n)}_3&…&x^{(n)}_{13}\end{pmatrix}\begin{pmatrix}0&0\\0&0\\0&0\\0&0\\0&0\\0&0\\0&0\\1&0\\0&1\\0&0\\0&0\\0&0\\0&0\end{pmatrix}=\begin{pmatrix}x^{(1)}_8&x^{(1)}_9\\x^{(2)}_8&x^{(2)}_9\\…&…\\x^{(n)}_8&x^{(n)}_9\end{pmatrix}}$$
つまり、特微量選択のパラメータはそれぞれどの特微量からきたか明確ですが、主成分分析のパラメータは、計算式はわかるものの、各パラメータ(例えば$${x^{(i)}_a}$$)に何の意味があるのかはよく分からないってことですね。
ちなみに当たり前かもしれませんが、新しいデータを変換するときは、X_trainの偏差を使って標準化し、上の行列式を掛けることで二次元に変換して変換します。
ということで、次元削減から主成分分析の説明までゆるふわにしてみました。思ったより大変だった・・・。けど僕の理解が進んだので良し!
で、次からまた「カーネル多変量解析」に入ります。カーネル主成分分析が次のテーマ。ではでは。
この記事が気に入ったらサポートをしてみませんか?
