勉強コラム 機械工学基礎編 2.無次元数

※自身の勉強まとめなので、ざっくりとした表現をしてわかりやすくしている部分もあります。正確な定義について知りたくなった場合は、教科書を参照しましょう。

・はじめに
　基礎編の1では単位と次元について勉強したので、ついでに無次元数について勉強しようと思います。無次元数は工学のいろいろなところで出てくるものであり、今回はとりあえず概念的な意義とよく出る無次元数について現状私の知っている無次元数について書いていこうと思います。「無次元化」については詳しくはないのでいつか書けるといいなと思います。

1．無次元数とは

　無次元数とは一言でいうと、単位がない数のことである（もう少し正確に表現すると、「同種の物理量で割った数」といことになるのかな？）。
　基礎編1.でSI基本単位と組立単位について記載したが、物理量はSI基本単位で表記することができる。ある物理量Qの次元はSI基本単位の次元の積で表現できる。

すべての物理量は基本単位の次元で表記できる。

a,b,c,d,e,f,gは定数

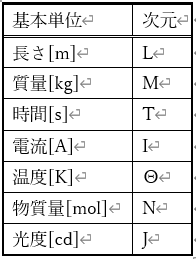
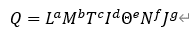
無次元数は次元が1になる数のことである（同種の物理量で割った値であるから、上式を見れば明らかですね。）。

2．無次元数の具体例

　機械工学で有名な無次元数はやはりレイノルズ数かなと思います。

レイノルズ数
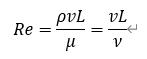
Re：レイノルズ数、ρ：密度[kg/m3]、ｖ：流速[m/s]、Ｌ：代表長さ[m]
μ：粘度[Pa·s]、ν：動粘度[m2/s]

 レイノルズ数は上式で表される数で「慣性力」と「粘性力」の比になります。よく、流体の流れが乱流か、層流か判断するときに出てきます。管内流では、数千以下では層流、超えると乱流になると一般的に言われています。（そのほかにも伝熱工学でNu（ヌセルト数）やPr（プラントル数）をやったな～と記憶しております。）
　このように無次元数はある状態を表すパラメータになります。無次元数を導入することで、物理挙動を表す指標になったり、異なる物理挙動を比較したりすることができるようになります。

3．まとめ

無次元数とは、
①次元が1になる数
②同種の物理量で割った数（比）、（何かの力）/（何かの力）とか。
③物理挙動や状態を表すパラメータで、異なる挙動を比較することができる。

4．あとがき

　無次元化についてとりあえずざっくりまとめようと思いましたが、あまりまとまっていませんね。自分自身「無次元化」について詳しくはないので、どうしても自分の抽象的なイメージでの書き方が多くなりました。今後勉強することで、もっとわかりやすく書けるよう努力しようと思いました。いつか「無次元化」について書きたいと思います。
　最後に、この記事で事実と自分の主観が混同してはいけないなーと思い、なるべく事実はである調、自分の主観はかっこ書きの中にですます調で記載していましたが、いちいち書き分けるのはめんどくさいので、今後は全部ですます調で混ぜて書こうかなと思います。

ご精読ありがとうございました。この記事がどこかの誰かの役に照れば光栄です。よろしければ、スキ、フォロー、シェアよろしくお願いいたします。