財政検証における経済前提の分布の見方

先日（12月25日）社会保障審議会の年金部会が開催され、8月に公表された財政検証に基づいて行われてきた、年金制度改革の議論についての整理が行われました。

最終的な改革案については、財政検証のオプション試算で示されたものからすると、正直物足りなさを感じるものですが、こちらのnoteでも度々書いた通り、様々な反対勢力の雑音でまともな議論がしづらい中、わずかでも改革を前進させたことは、「前のめりに倒れていった」と年金部会の権丈先生が評した通り、関係者の方々のご尽力の賜物として、今後のさらなる改革につながることを祈るばかりです。

さて、取りまとめられた年金改革の内容については、また後日触れることとして、今回は財政検証において用いられた経済前提について、気になることを発見したので、それについて書いてみます。

今日、証券アナリスト協会からのメルマガの中で、11月に開催された講演資料が紹介されていました。その講演とは、「日本財政を巡る課題-消費税10％以後の改革に向けて-」というテーマで、法政大学の小黒一正先生がお話しされたものです。

小黒先生は、財政検証に用いる経済前提に関する専門委員会の委員でいらっしゃったので、興味をもって資料を見ていたら、財政検証について用いられている6つの経済前提のうち、良い方の3つの実現性は低く、悪い方の3つが実現する可能性が高いと論じていました。

同じような内容の分析は、下のnoteでも読むことができます。

財政検証の経済前提が甘いというような批判はよくあるのですが、遠い将来のことを予測することは不可能であり、検証の結果は、あくまで良いものから悪いものまで幅広い経済前提によって将来の姿を投影（Projection）したものであって予測（Forecast）ではないとされています。

年金部会の専門委員会のメンバーである小黒先生が、この大前提に反するような形で財政検証の結果を評価することについて疑問を感じるのですが、それにも増して疑問に感じるのは、評価の方法についてです。以下に具体的に説明します。

小黒先生は、もともと財政検証の結果について、確率分布を用いた分析をしたいと考えている節があり、経済前提の6つのケースについても変数の一つである「全要素生産性（経済成長を生み出す要因の一つ）」について、過去の実績の分布を出して欲しいと委員会の事務局に要望を出していたようです。

そして、小黒先生の要望によって提出された資料が以下のものです。

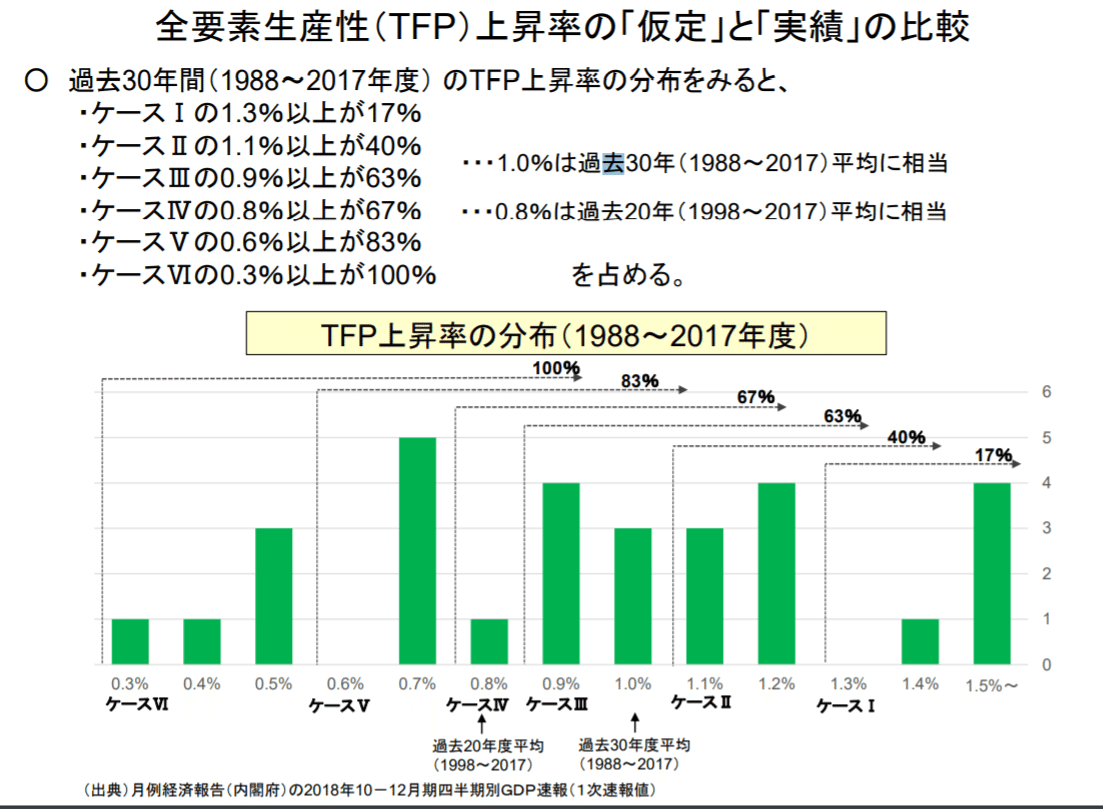
細かい説明は省きますが、私はこれを見て、「ケースⅢで想定されている全要素生産性（TFP）の0.9％は、過去20年～30年の平均値に近いものだな」と感じますが、小黒先生はどうも違うようで、以下のように見ていらっしゃいます（小黒先生のnoteに貼られていたレポートより抜粋）。

まず、「過去30年間（88～17年度）の実績の分布でみると、ケースⅢの0.9％は約6割（63％）がカバーされるシナリオに相当する」という意味は、過去30年間（88～17年度）のＴＦＰ上昇率のうち、TFP上昇率が0.9％以上になった年は全体の63％になったという意味である。
　しかしながら、これはケースⅢのシナリオが63％の確率で実現することを示すものではない。今後のTFP上昇率の分布がこれまでの分布と変わらないと仮定しても、ケースⅢのシナリオは63％の確率では実現しない。理由は単純で、ケースⅢは29年度以降のTFP上昇率が必ず毎年度0.9％以上であることを想定するもので、1年でもTFP上昇率が0.9％を下回ればケースⅢの前提を満たさないためである。
　これは次のような簡単なケースで明確に分かるはずだ。1年目のTFP上昇率が0.9％以上で、2年目のTFP上昇率も0.9％以上である確率はいくつか。数学のテストで、「63％の確率」と回答する学生がいるならば、「落第」である。各年度におけるTFP上昇率の確率変数が独立とすると、39.7％（＝0.63×0.63）が正しい確率になる。

この中で、「ケースⅢのシナリオは63％の確率では実現しない。理由は単純で、ケースⅢは29年度以降のTFP上昇率が必ず毎年度0.9％以上であることを想定するもので、1年でもTFP上昇率が0.9％を下回ればケースⅢの前提を満たさないためである。」として、50年間でケースⅢのTFP0.9％を維持する確率は、0.63の50乗でほぼゼロと結論付けています。

えっ？？？　ケースⅢで想定しているTFP0.9％って、長期においては0.9％を上回ることもあれば、下回ることもあり、それを馴らすと平均で0.9％ということではないのでしょうか？

単純なモデルで考えてみましょう。上のTFPの分布は山型の正規分布というよりも、平らな一様分布に近いように見えます。そこで、毎年発生するTFPの数値をサイコロの出目に置き換えて考えてみます。

サイコロを1回振った出目が3.5以上となる確率は、4と5と6が出た場合で50％です。それでは、サイコロを何回か振った場合、出た目の平均が3.5より大きくなる確率はいくつでしょう。3回振ったとして、小黒先生の考え方だと8分の1になります。でも、これは明らかにおかしいですよね。サイコロを何回振っても、その出目の平均が3.5以上となる確率は概ね50％です。

つまり、TFPの過去の分布に基づけば、長期におけるTFPの平均値が、ケースⅢで想定した0.9％以上となる確率は、小黒先生の計算のように小さくならないはずです。

先生のレポートは、今年の6月に週刊エコノミストに掲載されたもので、また11月の証券アナリスト協会での講演でも使用されています。おかしいと指摘がされていないということは、私の理解がおかしいのでしょうか？

どなたかお詳しい方がいらっしゃたら、（こっそり）教えて下さい。m(__)m