減法を説明するための闘い(3)｜孤高のトップランナーＫｒ社

　加減の説明の方法として、教科書は
パターン１）Ｋｒ社
パターン２）Ｔ社・Ｓ社・Ｄ社・Ｋｙ社・Ｎ社
パターン３）Ｇ社
の３つのパターンに大別できる。

　中学数学シェア１位、約４割の中学生がＫｒ社の教科書を持っている。Ｋr社の正負の数の加減の定義は他社と全く異なり、加減とは「○よりも△大きい数／小さい数を求める計算」であるとして、数直線上の移動に置き換えて答を求める。この説明方式をパターン１とする。

　他の各社がパターン２を採用する前は、他の各社の教科書もこのパターン１で説明がなされていた。つまり、Kr社のパターン１の説明は昔、他の各社も同様に行っていた方法なのである。

　そういう意味でこれが唯一に近い説明方法であったのかもしれない。

Ｋｒ社の減法への独自の道筋

Ｋｒ社の減法記述はあっさり

　Ｋｒ社の減法のページは「減法について学びましょう」から「正の数・負の数をひくには、符号を変えた数をたせばよい」のまとめまで１ページで、他の教科書のように図もない。減法の説明を見てみよう。

◎ひろげよう
次の［　］にあてはまる数を答えましょう。
（１）（＋９）－（＋３）は、＋９より［　］小さい数を求める計算で、
　　　これは、　　　　　　　＋９より［　］大きい数を求める計算と同じです。
（２）（－５）－（＋７）は、－５より［　］小さい数を求める計算で、
　　　これは、　　　　　　　－５より［　］大きい数を求める計算と同じです。
このことから、（１）、（２）の式を、たし算で表してみましょう。
　（＋９）－（＋２）＝（＋９）＋［　　］
　（－５）－（＋７）＝（－５）＋［　　］
　
上の◎から、正の数をひく計算は、
　（＋９）－（＋２）＝（＋９）＋（－２）
　（－５）－（＋７）＝（－５）＋（－７）
のように、負の数をたす計算になおすことができます。

（説明しよう）
　負の数をひく計算（－５）－（－７）が、正の数をたす計算（－５）＋（＋７）になおせることを説明しましょう。
（挿絵）人物１「正の数を引く計算と同じように考えてみよう」
　　　　人物２「－７小さい数を負の数を使わずに表すと…」

　このあと「符号を変えた数をたせばよい」とまとめて、次のページで２問例題を示したあと練習問題を並べて終わる。他社はどこも「減法」のセクションを設けているし、シェア２位のＴ社は３ページ、シェア３位のＧ社は５ページを割いている。

他の教科書にはない２つの準備

　しかし、Ｋｒ社の減法がアッサリ終わるにも伏線があり、ここに至るまでに準備が済んでいて、減法なので新しい概念や操作を導入する必要は、もうない、という状態になっているのである。

　その準備は２つあり、「数直線上で●より▲大きい数／▲小さい数を求めること」の練習であり、もうひとつは加法の解説の中で「負の数をたす計算⇒負の数分大きい数を求める計算⇒正の数分小さい数を求める計算」が済んでいることである。

　１つめ、Ｋｒ社は加減のセクションの前に、

　数の大小と数直線上の位置関係を使うと、ある数より大きい数や小さい数を、数直線を使って求めることができます。

として、数直線上で「●より▲大きい数／▲小さい数」を求める解説と練習をする。

　そして

　負の数を使って表されたことばは、例えば、
　　「－３大きい」を「３小さい」
のように、負の数を使わないで表すことができます。
　このことから、ある数より負の数だけ大きい数、小さい数についても考えることができます。

として、負の数だけ大きい数・小さい数を、正の数だけ小さい数・大きい数への変換ができることを、加減に入る前に済ましてしまっているのである。

　その上で、加法・減法のセクションに入り、それぞれを「●より▲大きい数／▲小さい数」を求める計算として定義して、式とその答について解説していく。

　例えば、
　　　　　５＋（－６）は、　５より《－６大きい数》を求める計算
　　（－２）＋（－６）は、－２より《－６大きい数》を求める計算
となり、数直線上では、次のようになります。
　　　　　　　（下図が挿入）
　したがって、
　　５＋（－６）＝－１、　　　（－２）＋（－６）＝－８
となります。

　ここまで準備が済んでいれば、減法は加法に転換できることはそこまで説明や練習はいらず、加法の練習も済んでいるので、むしろ意味を気にすることなく、減法を加法に転換する練習に集中すればよいのである。

　このパターン１のメリットは、たとえば「－３大きい数を求めることは、３小さい数を求めること」「－５小さい数を求めることは、５大きい数を求めること」と正の数での操作に変換できることである。ことで、これまで同様の操作で、特別な操作を追加することなく答を出すことができるわけである。

原理的に答は求められるが・・・

　しかし数直線上で「５小さい数」を求めるのは、原理的には数直線を１つ１つ辿って答を出したり、「１，０，－１，－２，－３」と数えて辿っていくことになる。指を折って数えるのとそうたいして違いはない。むろんこれでは、小数や分数の計算はできないし、そもそも答を出すのに時間がかかりすぎる。

　ところが、減法に入る前に、加法の符号の「同符号／異符号」に注目して、絶対値を小学校の計算で算出して符号をつける、というアルゴリズムを知っている。ここが終着点であることはパターン１でも変わらない。Ｋｒ社の指導書では

生徒が持っている、負の数などのイメージを大事にしていくことが必要である。その意味では、数直線や大小関係などを利用して十分にイメージを育んでから、生徒がイメージを離れても機械的に計算できるように二項演算としての和の規約という指導は理にかなっているといえる。

としている。つまり、まずは加法・減法のイメージを持ってから、機械的な計算方法として、先ほどのような計算方法に帰結していく、ということになる。

　この説明の仕方は自然にも感じるが、他の教科書がベクトルに基づく計算に移行していったのはやはりなにか理由が合ったのではないか。他の教科書と異なる点を探ってみることにする。

他の教科書と異なる点

演算オペレータという考え方

　「●よりも▲大きい／▲小さい数を求める」というやり方は、二項演算という考え方ではなく演算をオペレータとして見る見方であり、これは、パターン２やパターン３と大きく異なる点である。再び指導書から引用する。

　ここで、計算に対する見方についてまとめておこう。
　数の計算には、数の一方をオペレータとみる見方と2数を同等に扱う二項演算という見方がある。
　例えば、（ー7）＋5を、（ー7）より5大きい数を求めると考えて、５をたすというはたらきを中心に指導する場合がある。この場合、＋5は、５をたすという操作を表すものーーオペレータ（operator）として取り扱われる。
　それに対して、2数を同等に見てその和・積を求めるという二項演算としての見方がある。先に述べた絶対値と符号に注目した2数の和の規約（定義）は、0以上の整数の計算を前提として、整数における二項演算としての和を直接求めたものと見ることができる。
　計算結果を求めるにはどちらの見方をしてもよいが、計算そのものの見方としては、一方にかたよってはなるまい。
　前にも述べたように、教科書では、まずオペレータとしての和を体感させ、それをもとにして、二項演算としての2数の和の規約を導いている。
（啓林館　指導書　総論ｐ２３５）

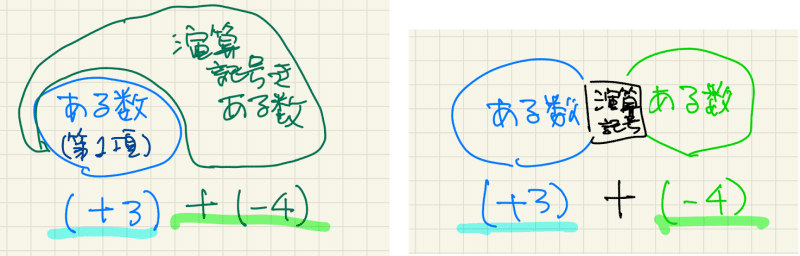
　Ｋｒ社の加法減法の定義は、「たされる数・ひかれる数」に対して操作を加えるオペレーターとしての演算として最初はとらえ、アルゴリズムとして便利な２項演算に持っていく。

（　）のある式・ない式

　もうひとつ、扱いが独特なのは（　）のある式である。Ｋｒ社は最初、－４より６大きい数を求める計算の式として
　　（－４）＋６
として、その計算結果を示したあとで、

　２数の加法の計算で、符号と絶対値に着目すると、どんなことがいえるでしょうか。符号に着目しやすくするために、ここでは、正の数にも符号をつけることにします。
（キャラクター吹きだし）　３＋６は（＋３）＋（＋６）とも表すよ

として
　　（－４）＋（＋６）
とする。これも、さきの「オペレータとしての見方」から「２項演算としての見方」への移行を表している。
　そして、代数和形式を「正の数に符号をつけずにあらわした式」とする。
（　）のある式・ない式の間を揺れながら前に進むのである。

　一方で他社は２項演算を基本に（　）をつけた式のみで続けたあと、最後に（　）と加法記号＋を省いた「項を並べた式（項だけを並べた式）」とする。

　これもＫｒ社の独自性と言ってよい。Ｋｒ社は、他社の説明原理とは一線を画しており、孤高なのである。ただ、代数和を正の数に符号をつけずにあらわした式と下のは、２１年度版からであり、この形式統一は定着するかどうか、歴史の淘汰が試されるような気はする。