
埼玉県追検査|公立高校入試統計問題2024
(問題1) 右の表は,あるクラスの生徒の睡眠時間を,度数分布表 に表したものです。睡眠時間の中央値が含まれる階級の相対度数を求めなさい。

(問題2) 次の文章を読んで,下の問に答えなさい。
紙飛行機を1回飛ばし,その飛行距離を競う大会が行われます。Tさんは,この大会に向けて,折り方が異なる2つの紙飛行機A,Bをつくり,飛行距離を調べる実験をそれぞれ30回ずつ行いました。実験の結果をヒストグラムに表すと,図1,2のようになり,飛行距離の平均値は,A,Bともに同じでした。
このヒストグラムでは,例えば,図1において,Aの飛行距離が6m以上7m未満の飛行回数は3回であることを表しています。

問 Tさんは,この大会で優勝を目指すために紙飛行機Aを選びました。Aを選ぶ理由を,図1,図2の特徴を比較して説明しなさい。

https://www.ac-illust.com/main/detail.php?id=205720&word=%E7%B4%99%E9%A3%9B%E8%A1%8C%E6%A9%9F
問題1
簡単そうな小問ですが,それでもいくつかの段階を踏まないと答えにたどり着きません。順を追ってやっていきましょう。
まず中央値です。データの値を小さい方から順に並べたときの中央にくる値で,この場合はデータの総数が40個で偶数ですから,中央にある2つの値,つまり【20】番目と【21】番目の平均値が中央値,ということになります。
ということは,中央値が含まれる階級について考える,ということは【20】番目と【21】番目のデータがふくまれる階級を考えるということになります。
それを度数分布表やヒストグラムで考えるときには,累積度数を考えるとよいです。
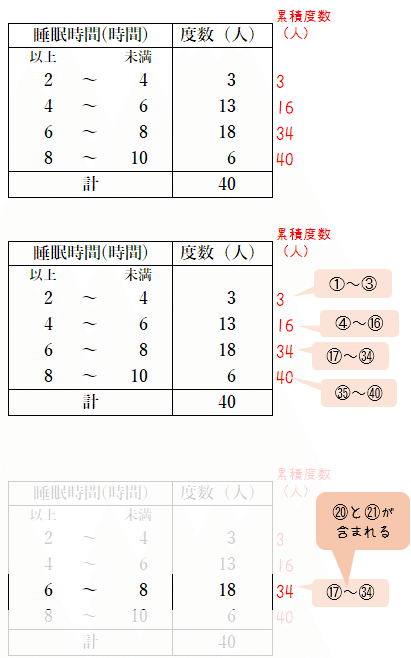
というわけで,睡眠時間の中央値が含まれる階級は6時間以上8時間未満,というところまでわかりました。
答えるのは,その階級の相対度数です。その階級の度数を,データの総数でわりますので,18÷40=0.45 となります。
問題2
この紙飛行機大会は,一発勝負です。とにかくできるだけ遠くに飛んだ方が勝ちです。
ヒストグラムを見ると,14m以上飛ぶのは,紙飛行機Aでは30回中4回に対し,紙飛行機Bでは1回しかありません。
Tさんは,Aの方が有利と考えたのでは,と想像できます。
ちなみに,紙飛行機Aでは30回中8回13m以上飛んでいるのに対し,紙飛行機Bでは4回です。
12m以上で見てみても,紙飛行機Aは30回中14回,実に半分ちかくですが,紙飛行機Bは8回。
これはTさんが優勝狙いで紙飛行機Aにかけるのもわかりますね。
答
(問題1)0.45
(問題2)(教育委員会の解答例)
14m以上飛んだ飛行回数は,紙飛行機Bより紙飛行機Aの方が多いから。※「12m以上」「13m以上」も正答とする。
この記事が気に入ったらサポートをしてみませんか?
