2020行動実験1の解説:ボルツマン、シュレーディンガー、ワトソン&クリック
以下の実験実習の1の解説である

ボルツマンの紹介:
オーストリー・ハンガリー帝国ウィーンに生まれた。1877年に発表した論文「熱平衡法則に関する力学的熱理論の第2主法則と確率計算の関係について」(L. Boltzmann: Wien Ber. 76, 373 (1877)) においてボルツマンの関係式を導き、それまでのカルノーらの研究によりマクロな熱力学の量であるエントロピーと、系を構成するミクロな構成要素がとりうる状態の個数との関係を導出した。このことにより、直接目に見えない原子や分子(やそれよりも小さい素粒子)などのふるまいを、マクロな量の測定や実験の結果の定量的な分析から理論的に解明することが可能になった。この仕事はアインシュタインによって1905年に、原子論の妥当性を裏付ける論文(この論文であつかわれた、ランダムウォークを扱う手法はのちのファイナンスにおける効率市場仮説へも応用されている)などへ影響を与えた。
ボルツマンの墓碑に刻まれているマイクロ・マクロ関係式(tuitionphysics.comより)

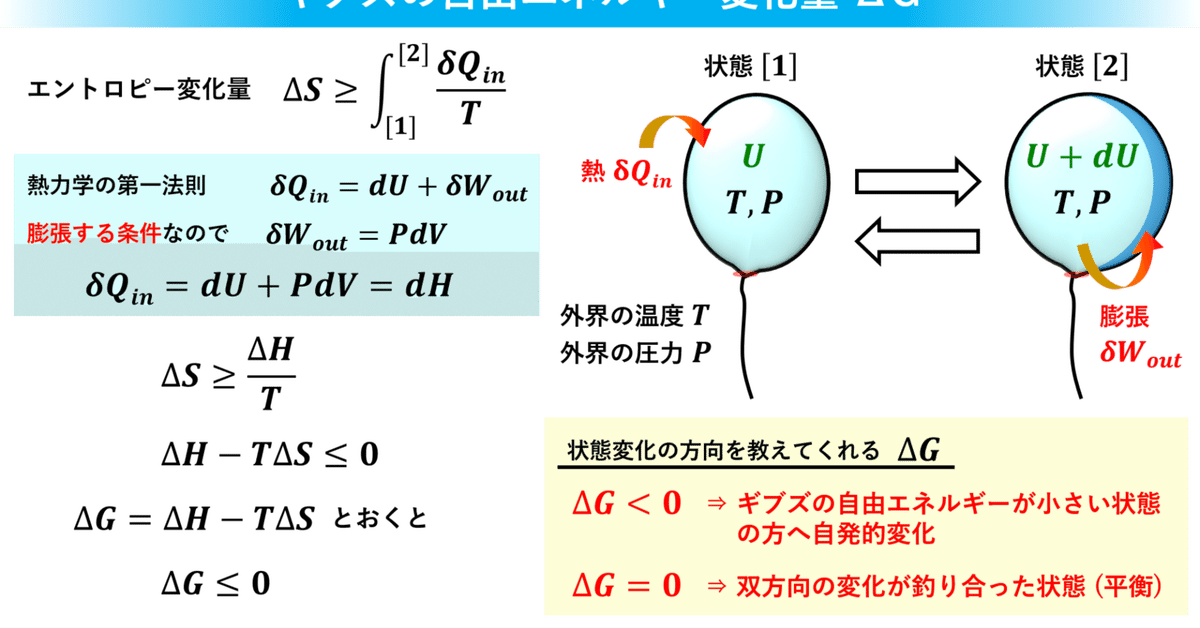
結果:伸ばした直後は熱さが、縮めた直後は冷たさが感じられるはず。
マクロな状況設定を確認しておくと、輪ゴムを(周囲と熱の出入りが自由なまま、すなわち断熱せずにただし、伸長の各時点では平衡equilibriumが成立しているようにして、つまり熱力学用語では、「準静非断熱的」に)急に伸ばしたり縮めたりする際には、その伸び縮みの前後の2状態で温度Tはどちらも室温と同じである(下記※参照)。それならばなぜ、伸ばした直後に唇に熱さが感じられ、縮めた直後に唇に冷たさが感じられるのだろうか。
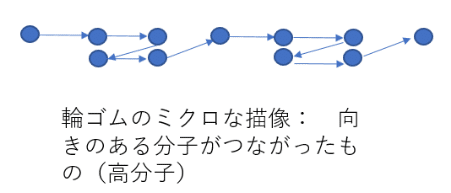
今回想定した、摩擦や散逸なく、左右に向きを変えることのできる分子がつながったゴムの概念図:
(自分で実験をしてみた際には、「ゴムを伸長または収縮させる際に、各時点で平衡状態を保ちつつ、可逆的に変化が生じるように」注意しなかったので、準静過程であるという想定で理論展開をするのは間違っているのではないか、と思う人もいるかもしれないが、この考えは理想的なゴムの場合には誤りである。変化の開始の状態と終了の状態がどちらも平衡状態であれば、実験操作の過程では実現していない仮想の(完全な)準静的過程に関する理論展開をおこなって得られた結論が、実験してみた際に起こるーーーおそらくは厳密には準静過程ではないーーーーマクロな変化の帰結に関する結論と、(実験操作において途中の過程が準静的であったかどうかにかかわらず)厳密に一致するからである。これは、熱力学というマクロ理論が、平衡(equilibrium)状態におけるマクロな状態量を記述する公理系であることを想起すれば、ロジカルに------すなわち、ゴムの伸長の途中で温度計を当ててみて数字を経時的に記録するなどといった無意味な追加的データ取得をおこなったり、今回の実験とは異なる他の実験データや観察データを参照してみたりといった余計なことをせずとも---演繹過程を進める際に1ステップごとにどこにも誤りが含まれないようにロジック操作を行うことで結論されることである。)
ここで、マクロな状態を記述する公理系である熱力学(thermodynamics)と、マクロとミクロをつなぐ統計力学(statistical mechanics)の知見を応用した直感的な解説を行う。
ボルツマンによって見出された、マクロな量とミクロな量
とを結びつける関係式をゴムの長さxを用いてあらわすと以下のものである。
命題1
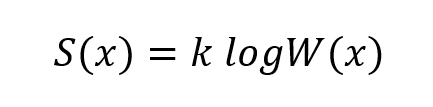
ただし、
熱力学的にはS(x)(単位は[J/K] ジュール・パー・ケルビンと読む Joule per Kelvin)はエントロピー(entropy)とよばれるマクロな状態量(マクロな状態---この例では長さxが一通りに定まれば、Sの実数値も一通りに定まるという意味)であり、W(x)はミクロな状態の数(そのマクロな状態には、ミクロにみるといくつ場合の数が存在するか)である。kはミクロ(右辺)とマクロ(左辺)をつなぐ普遍定数(ボルツマン定数 k = 1.380649×10^(−23) [J /K])である。ここで普遍定数と呼ぶ理由は、ミクロな構成要素自体の特性(構成要素が銅原子であるかどうかや、これから発見される未知の新粒子であるかどうかや、内部構造をもったものであるかどうか)に関係なくいかなる研究対象にとっても同一の数字1.380649×10^(−23)[ J /K]のまま、マクロな状態をただ一つに固定した場合のミクロな状態のありうる場合の数だけで右辺と左辺の比例関係が決まってしまう、という例外なき原理の定数だからである。
Sの次元(単位)とkの単位(次元)が一致しているので、右辺のWという変数は、単位がない「無次元量」であることがわかる(そうでないと左辺と右辺の次元が一致しないので物理学的に間違っている式になってしまうから)。すると、Wを測る1目盛の物理的意味が存在しないので、いかなる物理的計測装置(生物の感覚神経なども含む)を用意しても、Wが測れないということがわかる。このことから普通の意味で「W測定器」なるものが存在しえない、すなわち、体温計で体温(Kという単位を持つ量である)を測ったり、食物のカロリー量(Jやcalという単位を持つ量である)を食材を燃焼させてみて測る、というような素朴な意味において、直接的にはWは測ることができない物理量であるのだろうな、という推測ができる。
(歴史的逸話:実際、ボルツマンがこの式を発表した当時直面したのは、測れないような量が出現する数式を経験科学における永久不変の真理だと認めてよいのか、という批判であった。また、われわれのような生物体にとって、Wというミクロな状態の個数を、自分の手の指の本数を数えるように、視覚的に目で見て数えあげられてしまうほど原子や分子が大きくないという事実と矛盾しないような生命の原理とは何か(生物体にとってなぜ原子は見たり触ったりできないほど小さくあるべきなのか)、という問いを考察することによって、理論物理学者シュレーディンガーが、生物体の体長などのマクロな変数は、個々の細胞内の鎖状分子の配列の仕方というWのようなミクロなデータ形式として符号化(遺伝情報として)されているはずである---その分子のうち、多くの遺伝情報をコードする部分は非周期的な配列であるはずである----と演繹した(「生命とは何か―物理的にみた生細胞」E.シュレーディンガー)。以下は岩波書店 (2008/5/16) ISBN-10 : 4003394615 ISBN-13 : 978-4003394618の表紙:

ここからシュレーディンガーは、なぜカエルの子はカエルなのか、という生物学上の問いの答えは、遺伝情報が記録されているなんらかの生体内鎖状分子(当時はまだDNAが遺伝情報を担っていることは知られていなかった)の配列の仕方を、結晶を構成する原子間距離を測定する実験物理学の手法をもちいて研究することによって解明できるはずである、と熱統計力学と量子力学双方に矛盾が生じないロジック操作を重ねたうえで結論した。その著作を読んだ(当初は)鳥類学者だったジェームズ・ワトソンが、おそらくシュレーディンガーが述べている鎖状分子は、細胞核内の染色体を構成しているDNAなのであろう、と考えて、当時は物理学の大学院生だったフランシス・クリックと議論を行い、DNAの構造決定の研究をはじめた、ということも生物学の歴史でよく知られている)。以下はDNAの著作権フリー画像。

また、同様の次元解析によって、Sの値を求めるには、概念上は、温度計とカロリー計とを用意して、何かの実験操作の際にそれらの目盛りの数字の割り算をすればよいのだな、ということが推測できる。しかし、右辺のWに数字を代入してlogをとってkを掛け算してSを求める必要がある場合には、直接Wを測ってしまって得られた数字を右辺に代入する、というお手軽な方法をもちいることができず、Wの数字を、測定データを用いずに何らかの数学的思考過程によって理論計算してからそれを右辺のWに代入して左辺のSを求めなければいけないのだな、ということもこの次元解析を行った段階ですでに見通せるであろう。
このように、命題1を用いるとミクロな性質とマクロな性質をを結びつけることができるようになるが、命題1自体をミクロな法則からロジカルに演繹することはできない。したがって、「なぜ」という問いをそれ以上推し進められないという意味で命題1は「究極」の原理の一つである。下図の著作「マクロな体系の論理」(吉岡大二郎)のまえがきを参照のこと:
http://daijiroyoshioka.sakura.ne.jp/stpbook/stp_preface.pdf

また、上図のような今の設定(ゴムの温度が一定でエントロピーや熱がゴムと唇の間で移動可能な(つまり非断熱的な)準静過程のマクロな性質としては、
命題2
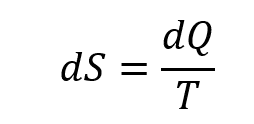
が成立することが、平衡状態のマクロな量の間の関係、ミクロな量に言及することなく記述する熱力学の公理たちから数学的に演繹できる(今、ゴムの各構成要素は、摩擦や散逸なく左右に向きを変えることができると理想化しているため、両辺の間に等号が成立する)。ただし、左辺は状態量であるエントロピーの変化量、右辺は出入りする熱(これは状態量ではない)の量を変化の前後で一定の温度という状態量で割ったものである。(Qは譲渡・転売可能な著作権のようなもの、TやSは譲渡・転売不可能な著作者人格権のようなものである)
(この式を一瞥して、概念的な間違いがないことを確認しておこう。左辺は[J/K]という単位をもち、右辺は[J]という単位を持つ量を[K]という単位をもつ変数で割り算しているので、左辺と右辺の単位が一致しているので、物理学的に間違った式ではないだろう、とか、ボルツマン定数kというミクロとマクロをつなぐ普遍定数がこの関係式のどこにも出現していない、ということが、この式がマクロな3変数S,Q,Tたちの間の関係を規定しているのであって、ミクロとマクロをつなぐという意味性を帯びていない、という概念的性質と矛盾していないので、ここまでの理論展開においてロジック矛盾が生じていないのだろう、といったことがすぐに見て取れるであろう)
今の例では、ゴムのエントロピーが減少すると、その減少したエントロピー量に室温を掛け算した大きさの「熱」が周りに放出される(唇を接触させていると暖かく感じる)、という関係式である。(反対に、エントロピーが増大すると、そのエントロピーの増大分に室温を掛け算した大きさの数字の熱量が周りから吸収されるので、ゴムに唇を接触させていると冷たく感じる)
まとめると、以下の場合分けとなる:
dS>0⇒dQ>0(ゴムへ熱が流入、流入元は唇)⇒唇に冷たさを感じる
dS<0⇒dQ<0(ゴムから熱が流出、流出先は唇)⇒唇に温かさを感じる
以上の命題1と2とをゴムの内部構造を考慮して結合すると、実験結果が説明できる。
--------------------------------------------------------------------------------------
唇で感じ取ることができるのは、熱さ(ゴムのdQ<0)または冷たさ(ゴムのdQ>0)であって、ゴムのWやそれによって決まるエントロピーやその変化ではないので、今回の実験に関しては上記の1⃣「Wの数字を、測定データを用いずに何らかの数学的思考過程によって理論計算して」から2⃣「それを右辺のWに代入して左辺のSを求め」るという2段階の手順が、データの解釈のために必要である。さらに3⃣「長さxの関数としてS(x)を微分して、ゴムが伸びるとエントロピーが増えるか減るかを判断」(dSの正負を判定)し、最後に命題2を用いて4⃣ゴムが伸びた場合と縮んだ場合のdQの符号がプラスかマイナスか、を判定すればよい。
1⃣/*上記の「Wの数字を、測定データを用いずに何らかの数学的思考過程によって理論計算」はここから*/
ゴムを構成する一分子の長さをaとする。また簡単のため、各分子は左向き
か右向きかどちらか一方のミクロな状態しかとらないものとする。
右向き分子がr個、左向き分子がl個だとすると、全体の長さxは、x=(r-l)a であり、全分子数は、n=r+lである。
ミクロな場合の数Wは、全部でn個あるうちからr個を
選ぶ組み合わせが何通りあるか、という場合の数なので、
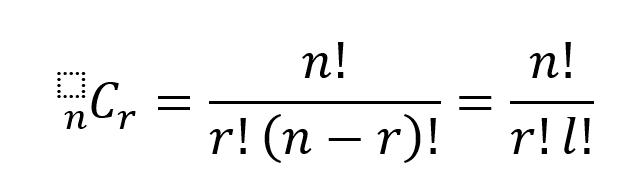
である。この式はミクロに見た式であるが、今、興味があるのはマクロな性質であるため、nが非常に大きいときに成立するスターリングの公式n!≅n^nをもちいると、
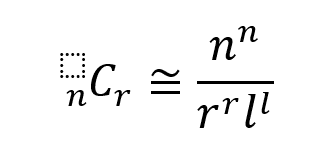
となる。以上の議論では、直接測定できない(見たり触ったりもできない)ミクロな量であるa,n,r,lという量のみを用いて、マクロな状態一つ(←これは測定できる)に備わっている、ミクロな状態の可能性をすべて数え上げることに成功した、という点が重要である。
/*上記の「Wの数字を、測定データを用いずに何らかの数学的思考過程によって理論計算」はここまで */
2⃣/*上記の「それを右辺のWに代入して左辺のSを求め」はここから */
今、
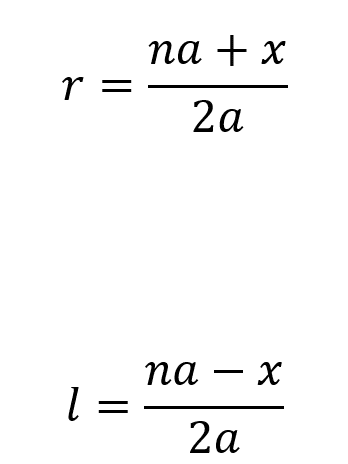
が成立しているので、命題1より、右辺がミクロなままである以下の式を、
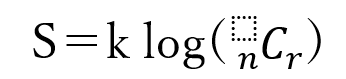
マクロな量であるゴム長xの関数として左辺だけでなく右辺もマクロな量xであらわすことができる。(注意:下記の式の右辺に出てくるn(ゴムを構成する分子の個数)やa(分子の長さ)はミクロな量なので、右辺はマクロな変数だけであらわされているわけではないのでは?と一見して誤解する人もいるかもしれないが、nとaの積はゴムの最大長というマクロな変数であり、nやaはこの積の形でしか右辺に登場していないので、この式はゴムの長さ、最大長という2種類のマクロ変数だけでエントロピーが表せたということである)

/*上記の「それを右辺のWに代入して左辺のSを求め」はここまで */
3⃣この、エントロピーがゴムの長さxによってどのように変化するか、xで微分して調べてみるということを実際に行ってみると、
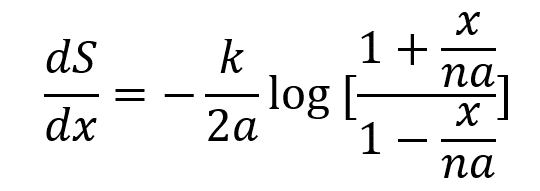
である。ここで、ゴムが最大に伸び切った長さnaよりもxが非常に小さい場合の近似を用いると、
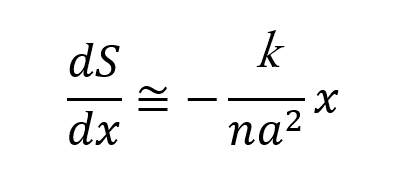
となり、ゴムが長いほど(xが大きいほど)エントロピーが減少することがわかる。(ゴムが長さaの分子3個でできているという特殊なケースを以下に図解した)

4⃣ここで命題2を思い出すと、ゴムが引き延ばされた時には、(ゴムの温度は上昇せずに)周りへ熱が放出され(dQ<0)、唇に温かさが感じられ、ゴムが縮められたときには、(ゴムの温度は低下せずに)周りから熱が奪われて(ゴムのdQ>0)唇に冷たさが感じられる、ということが演繹される。
以上、久保亮吾「大学演習 熱学・統計力学」第5章〔A〕【13】,および吉岡大二郎「マクロな体系の論理」(岩波)を参考にした。
※ここで考察したようなマクロ条件と異なり、断熱材で囲んで周りと熱やエントロピーのやりとりがおこらないようにして伸長させる(断熱的過程の)場合に、伸長によってゴムの温度上昇が起こることの説明は、京都大学教授・佐々真一氏による著作「熱力学入門」6.4節を参照すること。(ただし、準静的変化と断熱変化とは、異なる物理過程であることに注意すること。)
また、この例は理想化したゴムであるが、実在するゴムでは、いわゆる内部エネルギーの変化や散逸なども熱の出入りに寄与する。とくに、摩擦熱の発生や散逸は、不可逆過程を引き起こす。このあたりは、非平衡統計力学の金成主先生からコメントいただいた。また、実在するゴムに関する実験結果も、大阪大学により、以下に公開されている。
大阪大学の実験データ(松尾隆佑氏,佐藤尚弘氏による執筆 2020年12月23日訪問):
http://www.chem.sci.osaka-u.ac.jp/lab/micro//report/rcst/2013/2013res17.html.ja
----------------------------------------------------------------------------------
レポート課題
ゴムではなく、空気などの気体のエントロピーは、命題1を用いてゴムの場合の1⃣と2⃣のステップをミクロな観点にまず立って実際に行ってWを計算し、それからS=k log Wというボルツマンの原理に代入してSを体積というマクロな変数として表現すると、(単純に理想化した場合)、体積Vの関数として
命題1’ S(V)=k log[ V×(Vによらないミクロな量)]
である。 また、[ ]内は無次元量、つまり(Vによらないミクロ量)は[1/体積]という次元をもつ。
(↑これは命題1から、ゴムのようにつながった分子の鎖の性質を考慮する代わりに、気体の統計力学的性質を考慮して計算すると得られるが、今回はその考慮過程はおこなわず、この式を用いて考察するだけでもよい)
熱が出入りできるけれども気体分子は出入りできない材質でできたピストンに入ったこの気体を、ピストンを引っ張って引き延ばすと、唇に感じるのは、温かさか、または冷たさか、どちらであるかを、理由とともに答えよ。
ヒント:(理想的ゴム特有の式S=klog(nCr)の代わりに)命題1’ と命題2(ゴムでも気体でも成立するdQ=dS/T)とを組み合わせて推論すればよい。つまり、ゴムの場合の3⃣の考察を、
命題1’ S(V)=k log[ V×(Vによらないミクロな量)]に関してVに関する微分を用いる(必要な公式は(log x)'=1/x, ただし対数の底はeとする)か、または下のグラフを読み取って行えばよい。
それから4⃣のように命題2を想起すれば、dQの符号が判明する。気体のdQ>0⇒唇は冷たく感じる、気体のdQ<0⇒唇は暖かく感じる、である。
また、命題1’の定性的な性質は、直感的に結論することもできる。気体は空間内に多数の原子分子が相互作用せずにただよっているという存在形態なので、大きい部屋(V大)と小さい部屋(V小)とでは、同じ個数の小物の配置の仕方(=W)はどちらが多いか?と考えれば、体積が増えるとSが増えるのか減るのかがわかるだろう。
◆参考◆(受講生から、logの中身に関する質問があったので追加情報提供):命題1から命題1’を求める際に、ゴムの場合と同じように、ミクロな観点にたって(ただしミクロな状態の測定はできないので、ミクロな法則に基づいた数学的思考によって)理想気体のWを数え上げて気体のSを求めた場合のミクロな右辺でマクロな左辺Sを求めた結果は、北大理学部による下記の解説22式に記載されている:
a log x + b log y +c log z = log[(x^a) (y ^b) (z^c)]、5/2=log [e^(5/2)]という式を使えば、22式が S=klog[V×(Vによらないミクロな量)]の形になっている(ただし気体の全分子の個数をダースのような単位として個数を測ることにしてN=1としている)ことがわかるであろう。
また、このようにWをミクロ的に計算した結果から、マクロな実験・理論的考察しかできなかった時代に、ロバート・ボイルらの実験によってすでに見つかっていたpV=nRTという、マクロな変数同士(それゆえkが出現していない)の実験式(実験データから式が特定された時代にはデータに合うから正しいということはわかっていたけれど、なぜこの式になるのかはわからなかった、気体の状態方程式と呼ばれるもの)が、S=klogWというボルツマンの原理を利用すると、導出できる(なぜ気体の状態方程式が正しいのかがわかるーーーつまり「なぜ」という問いを繰り返してこのボルツマンの原理にたどり着いたので、それ以上、疑問を推し進めることは不毛となる)ことも、この解説ではp.4下から3行目で説明されている(ただし、統計力学・量子力学・解析力学(ハミルトン形式)という3つの公理系の理解が、読解のためにあらかじめ必要であるため、はじめて熱統計力学の実験データを解析する場合には不向きである。そのため、この講義では、より初等的にWが計算できるゴムの例を、上記においてW=nCrとなる計算過程を示した)。
「古典理想気体の統計力学」(北大理学部物理学科・北孝文先生による解説)
http://phys.sci.hokudai.ac.jp/~kita/StatisticalMechanicsI/Stat5.pdf
(2020年12月24日訪問)
◆参考ここまで◆
(注:対数関数のグラフは以下のように、引数(独立変数、xは今の場合は体積V)の増加関数である)
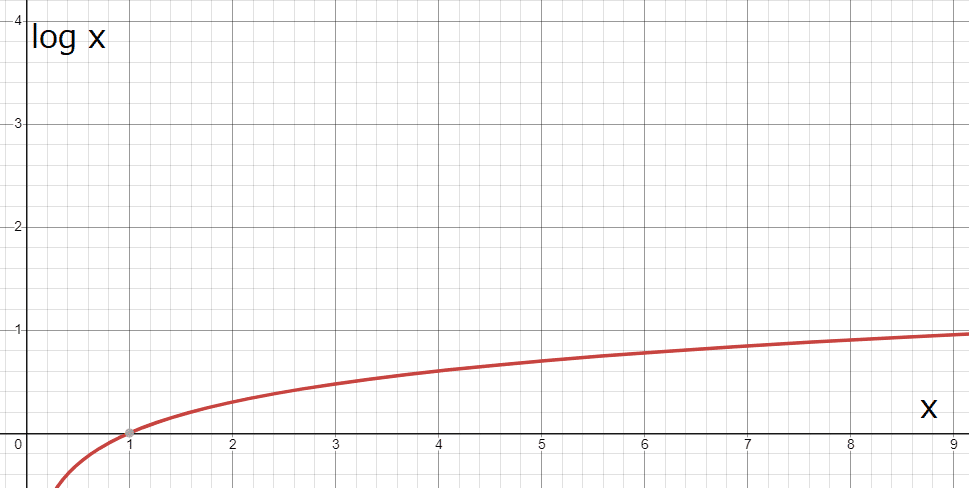
(実在気体のエントロピーは体積以外の寄与も存在するので、実在する気体のエントロピーは0より小さくはならない。そうでないといわゆる熱力学第三法則が成立しなくなってしまうが、このレポート課題ではその点に関する考察は省略してよい。)
おまけ:もし、ゴムを力任せに引っ張って、途中が準静的過程でないように実験をした場合には、はじめとおわりのゴムの温度が室温Tだったとして、途中の温度はそれより高温か、低温か、と問われたら、どう答えればよいだろうか。
また、今回の分析(ゴムと気体のマクロな外力に対するマクロな反応の比較)は、たとえば以下のような社会に関する問いとも関係するだろう。

---------------------------------------------------------------------------
参考:
熱力学におけるマクスウェル関係式-------マクロな量の微係数の関係式ーーーーを用いると、ゴムの張力がヘルムホルツ自由エネルギーの2階微分の係数から求められ、[kT/(na^2)]x という、引き伸ばした長さに比例する(フックの法則)が得られる。ミクロな考察に立ち入らなくても、マクロな量の数式変形だけで、力に関する理解(関係式)が得られることが重要。ここで用いられる自由エネルギーは、計算論的神経科学分野で脳における計算・予測モデルとして情報科学のシャノン・エントロピーと組み合わせて用いられることがある (神経科学者Karl Fristonによる自由エネルギーの式を用いた脳の理論など)。
以上の例のように、ミクロな構成要素の特性によらず、マクロな量たちの間に法則性が成立することや、その法則を演繹できる記述的公理系を、創発性(emergency)原理などと呼ぶことがある(ノーベル物理学賞受賞者 フィリップ・アンダーソンによる: More is different)
・東京大学物性研究所によるフィリップ・アンダーソンの訃報
・フィリップ・アンダーソンらが設立した複雑系の研究所(サンタフェ研)による訃報
ここで紹介した現象の身近な応用例として、伸長発熱素材を用いたスポーツウェアがある。(旭化成などが実用化)
熱力学という、マクロな系を記述する公理系がどのようなものか興味がある人は以下の論文を参照のこと(ただし、初心者に難解)。
The Physics and Mathematics of the Second Law of Thermodynamics
Elliott H. Lieb, Jakob Yngvason
Journal reference: Phys.Rept. 310 (1999) 1-96
DOI: 10.1016/S0370-1573(98)00082-9
Report number: EHLJY 05/Jan/99
Cite as: arXiv:cond-mat/9708200 [cond-mat.soft]
(or arXiv:cond-mat/9708200v2 [cond-mat.soft] for this version)
(マクロ系を記述するエントロピーの公理の部分を抜粋)

ゲシュタルト心理学:
ヴントの還元主義的心理学に対して、熱統計力学のような創発主義的心理学として,ボルツマン、シュレーディンガーらと同じく、オーストリー・ハンガリー帝国に生まれたヴェルトハイマーらによって発展させられた心理学。たとえば下記のような視覚刺激に対する知覚を研究する。表面的に感知したマクロな知覚印象の背後には、知覚印象の性質とは全く異なる性質をもったミクロな構成要素たちが存在するかもしれない(しかしその構成要素のミクロな性質は知覚される「マクロな」パターンよりも知覚されにくい)という点に、S=klogWの左辺(感じられるマクロな世界の量)とW(目に見えないミクロな原子の世界の量)との関係とのアナロジーを感じる人もいるだろう。この心理学派の中から、レヴィンによる「集団力学」(グループダイナミックス)というサブジャンルが派生した。
(引用元:”Gestalt Psychology” http://psychology.iresearchnet.com/gestalt-psychology/ 2020年12月23日訪問)

熱統計力学をソーシャルメディアに応用した研究を紹介している本:
高安美佐子・著「ソーシャルメディアの経済物理学 ウェブから読み解く人間行動」日本評論社
ISBN-10 : 4535556784
ISBN-13 : 978-4535556782

熱統計力学の考え方を、判断や意思決定の分野へ応用している本:
岩波講座 物理の世界 物理と情報〈3〉ベイズ統計と統計物理
伊庭 幸人
ISBN-10 : 4000111582
ISBN-13 : 978-4000111584

熱統計力学と機械学習の関連、ボルツマン・マシン
などについての、
大関真之 先生
京都大学 大学院情報学研究科システム科学専攻
による解説
「知的情報処理の統計力学
―機械学習を始めてみよう―」
この記事が気に入ったらサポートをしてみませんか?
