
画像解析を高速化させるためのTipsわかりやすくまとめてみた(2)
前回は、整数型での四捨五入の話をしました。整数型のみで計算をすれば浮動小数点型を使うよりも(ちょっとだけ)速く計算できますよという話でした。
前回の整数型演算の話の延長で、今回は、固定小数点数の話をします。(SIMDの話は、次回以降にします。)
固定小数点数とは
通常、コンピュータで小数を表現する手段として浮動小数点数(float型とか、double型とか)で表現しますが、限られたビット数で高速に計算しないといけない場合(画像って8bit整数などで表現されていますよね)などには、固定小数点数を使います。
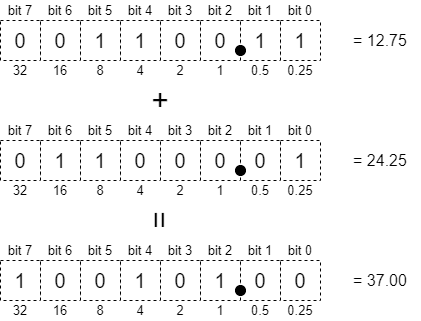
固定小数点数は、小数点の位置が固定されている数の表現で、例えば、8bitのうち下から2つ目に小数点を置くと決めた場合、2進数で 001100.11 のように表現ができ、これは10進数で 12.75 を意味します。

固定小数点数型というのが、CPUやプログラミング言語に用意されているわけではなく、実際には、整数型(int型とか)を用いてプログラミングします。
四則演算
固定小数点数で四則演算をする場合、いくつかの法則があります。
足し算や引き算する場合は、そのまま整数同士の足し算・引き算で計算できます。
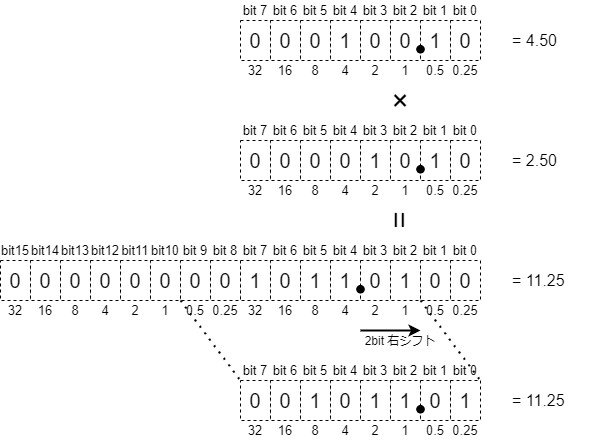
掛け算や割り算の場合は、計算した結果の小数点の位置がずれるので、小数点の位置をシフト演算で調整します。
割り算を使わない割り算
割り算は、結構重たい処理なので、除数が固定されているなどの場合は、除数の逆数の乗算でおこなったします。
つまり、ans = x / y を計算したいときには、r = 1 / y を前もって計算しておき、ans = x * r を計算するようにします。
これを、固定小数点数で計算する場合は、以下のようにします。
// x,yの範囲 (0~255) のビット数
int n = 8;
// 固定小数点数の小数部のビット数
int q = 2 * n;
// 除数
int y = 9;
// 除数の逆数 (固定小数点数) をあらかじめ計算しておく
int r = (1 << q) / y;
int div_int(int x, int r)
{
// 被除数に除数の逆数を掛ける + 誤差の補正
int a = x * r + (1 << n);
// 右シフトして小数部を切り捨てる
int ans = a >> q;
return ans;
}なぜ今回、固定小数点数での割り算を使わない割り算の話をしたかというと、実は、SSE(IntelのSIMD)には整数型の割り算がないので、固定小数点数の割り算を使わない割り算の話をしておかないと、SIMDの話できないということに気づいたわけで…
というわけで、次回、SIMDの話をします。(予定)
メンバー募集中です
アダコテックは上記のような画像処理技術を使って、大手メーカーの検査ラインを自動化するソフトウェアを開発している会社です。
機械学習や画像処理の内部ロジックに興味がある方、ご連絡下さい!
我々と一緒にモノづくりに革新を起こしましょう!
この記事が気に入ったらサポートをしてみませんか?
