
2次元配列管理クラスの実装について
今回はゲーム作りに役立つ2次元配列管理クラスを紹介します。
2次元配列は、2Dゲームにおけるマップ(フィールド)データを格納するためによく使われます。
例えば落ちものパズルゲームでは、各色のブロックを2次元配列の数値データとして扱います。
過去にQiitaに書いた記事では、Tiled Map Editorというマップエディタで作成したデータをこのクラスに格納したり……
A*での経路探索をする際に、このクラスを使って経路情報を求める、という使い方をしていました。
他にもパズルゲームの情報を格納することにも使えます。
生の配列を使っても問題ないですが、クラスをかぶせることで、領域外参照によるエラーを未然に防ぐ、設定している情報をデバッグ出力して簡単に確認することができます。
■C# (Unity) での実装
using UnityEngine;
using System.Collections;
/// 2次配列管理
public class Array2D {
int _width; // 幅
int _height; // 高さ
int _outOfRange = -1; // 領域外を指定した時の値
int[] _values = null; // マップデータ
/// 幅
public int Width {
get { return _width; }
}
/// 高さ
public int Height {
get { return _height; }
}
/// 作成
public void Create(int width, int height) {
_width = width;
_height = height;
_values = new int[Width * Height];
}
/// 座標をインデックスに変換する
public int ToIdx(int x, int y) {
return x + (y * Width);
}
/// 領域外かどうかチェックする
public bool IsOutOfRange(int x, int y) {
if(x < 0 || x >= Width) { return true; }
if(y < 0 || y >= Height) { return true; }
// 領域内
return false;
}
/// 値の取得
// @param x X座標
// @param y Y座標
// @return 指定の座標の値(領域外を指定したら_outOfRangeを返す)
public int Get(int x, int y) {
if(IsOutOfRange(x, y)) {
return _outOfRange;
}
return _values[y * Width + x];
}
/// 値の設定
// @param x X座標
// @param y Y座標
// @param v 設定する値
public void Set(int x, int y, int v) {
if(IsOutOfRange(x, y)) {
// 領域外を指定した
return;
}
_values[y * Width + x] = v;
}
/// デバッグ出力
public void Dump() {
Debug.Log("[Array2D] (w,h)=("+Width+","+Height+")");
for(int y = 0; y < Height; y++) {
string s = "";
for(int x = 0; x < Width; x++) {
s += Get(x, y) + ",";
}
Debug.Log(s);
}
}
}■Pythonでの実装
import random
class Array2D:
def __init__(self, width, height):
self.create(width, height)
self.outofrange = -1 # 領域外を指定したときの値
def create(self, width, height):
# 作成
self.width = width # 幅
self.height = height # 高さ
self.vals = [0] * width * height # 値
def to_idx(self, x, y):
# 座標をインデックスに変換する
return x + (y * self.width)
def check(self, x, y):
# 領域内チェック
if 0 <= x < self.width:
if 0 <= y < self.height:
# 領域内
return True
return False # 領域外
def check_from_idx(self, idx):
# 領域内チェック (インデックス指定)
return 0 <= idx < (self.width * self.height)
def get(self, x, y):
# 値の取得
if self.check(x, y) == False:
return self.outofrange
return self.get_from_idx(self.to_idx(x, y))
def set(self, x, y, v):
# 値の設定
if self.check(x, y) == False:
return
return self.set_from_idx(self.to_idx(x, y), v)
def get_from_idx(self, idx):
# 値の取得 (インデックス指定)
if self.check_from_idx(idx) == False:
return self.outofrange
return self.vals[idx]
def set_from_idx(self, idx, v):
# 値の設定 (インデックス指定)
if self.check_from_idx(idx) == False:
return
self.vals[idx] = v
def choice(self, v):
# 指定の値が存在する座標をランダムで取得する
list = []
for j in range(self.height):
for i in range(self.width):
if self.get(i, j) == v:
list.append((i, j))
if len(list) == 0:
# 存在しない
return -1, -1
return random.choices(list)
def fill(self, v):
# 全てを指定の値で埋める
self.foreach(lambda x, y, val: self.set(x, y, v))
def foreach(self, func):
# 繰り返し処理を行う
for j in range(self.height):
for i in range(self.width):
func(i, j, self.get(i, j))
def dump(self):
# デバッグ出力
print("[Array2D] (w,h)=(%d,%d)"%(self.width, self.height))
for j in range(self.height):
s = ""
for i in range(self.width):
s = s + "%d,"%self.get(i, j)
print(s)
テストコード
# テストコード
array2d = Array2D(8, 8) # 8x8で作成
array2d.set(1, 2, 5) # (1, 2) に 5を設定
array2d.set(3, 7, 3) # (3, 7) に 3を設定
array2d.dump() # デバッグ出力
↓↓↓↓↓↓↓↓↓ 出力結果 ↓↓↓↓↓↓↓↓↓↓↓
[Array2D] (w,h)=(8,8)
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,5,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,3,0,0,0,0,■コードの説明
このクラスでは座標系を 「X・Yの直交座標系」と「インデックス座標系」の2つからアクセスできるようにしています。

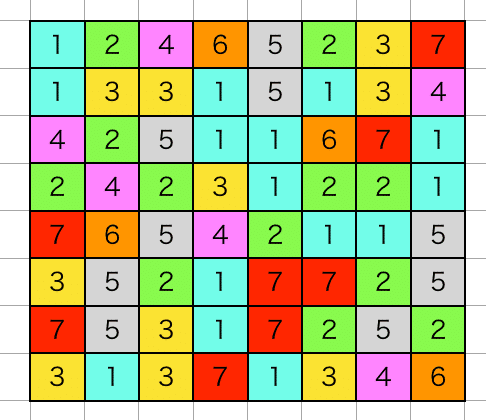
直交座標系であれば、例えば「赤色」の座標は (x, y) = (2, 3)、「水色」の座標は (x, y) = (7, 5) でアクセスすることができます。

これに対してインデックス座標系 (これは私の造語です) では、アクセスするための値は一次元の通し番号となります。左上から開始して1ずつ増加していき、右端で折り返します。
直交座標系でいう (x, y) = (2, 3) は "29"(赤色の座標)、(x, y) = (7, 5) は "52" (水色の座標)となります。
直交座標系とインデックス座標系は相互に変換が可能です。
▼直交座標系からインデックス座標系への変換
* インデックス座標 = x + (y * 幅)
▼インデックス座標から直交座標系への変換
* X座標 = インデックス座標 % 幅 (※剰余を求める)
* Y座標 = インデックス座標 ÷ 幅 (端数は切り捨てます)
例えば、赤色の座標は (x, y) = (2, 3) なので、インデックス座標は 2 + (3 * 9) = 29となります。
水色のインデックス座標は52なので、X座標は 52%9 = 7、Y座標は 52÷9 = 5となります。
■2次元配列クラスのさらなる拡張について
このクラスはゲーム内容によって、拡張をするのも良いです。
パズルゲームで下からブロックが迫り上がる
→各段の要素を1段上にずらす機能を作る
パズルゲームで、特定の位置のブロックを消すと、上下左右の全てのブロックを破壊する
→1列、1行まとめて消す関数を追加する
空いている場所 (例えば "0") をランダムで探す
→空いている場所に敵やアイテムをポップする、という使い方ができます
2次元配列を使いこなすと、作れるゲームの幅が広がります。
と、ここまで書いて気がついたのですが、内部データの持ち方は1次元でしたね……
◾️関連する記事
2次元配列のデータを利用した、落ちものパズルゲームの作り方をまとめてみました。ブロック消去ルールの実装方法が中心となっています。
