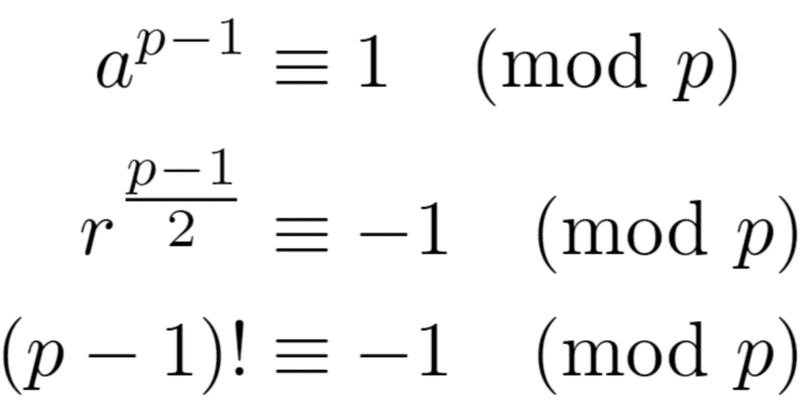
原始根でウィルソンの定理を証明する!
まず始めに、今回の内容はマロが高木貞治さんの『初等整数論講義〔第二版〕』の第一章を読んだときに個人的に感動した証明を紹介します。さらに詳しく内容を知りたい方は是非読んでみてください!
マロ:やっと春休みが終わるね!
ミケ:もっと休みたかったな~…
マロ:(笑)
ミケ:春休みなんかした?
マロ:強いて言うなら『初等整数論講義』読んだ!
ミケ:おぉ、あの高木貞治さんの?!
マロ:そう!その中でウィルソンの定理の証明が紹介されてたんだけど個人的にめちゃくちゃよかった!
ミケ:お、聞かせて!
ウィルソンの定理について
まず、ウィルソンの定理は素数に関する定理なんだけど、
$${p}$$ が素数ならば $${(p − 1)! ≡ −1 \pmod p}$$ が成り立つ。
逆に、整数 $${p > 1 }$$に対し、$${(p − 1)! ≡ −1 \pmod p}$$ ならば、$${p}$$ は素数である。
例えば、$${p=5}$$の時は、
$${(5-1)!=4\times3\times2\times1=24≡-1\pmod 5}$$
で、確かにあってるね!
$${p=7}$$の時でも、
$${(7-1)!=6\times5\times4\times3\times2\times1=720≡-1\pmod 7}$$
で、あってるね!
じゃあこの定理の証明を使用!
…の前にその証明を理解するために必要な知識を紹介するね!
合同式(≡)について
さっきから出てくる$${≡}$$ていう記号があるね。中学校で図形の合同を表すときに使ってた記号だね!
「数字の合同って何なんだよ!」って思うかもしれないけど、合同式はある数字$${m}$$で割ったあまりが等しい数字$${a,\ b}$$を$${≡}$$でつないでいるんだよね。
例えば、$${10,\ 28}$$は$${9}$$でわるとどっちもあまりが$${1}$$だから、
$${10≡28\pmod 9}$$
って表すんだよね!それで合同式は足し算と引き算と掛け算は今まで通りに計算しても大丈夫!でも割り算はいろいろ制約があって普通にはできないんだよね。
ここら辺のもう少し詳しい内容は次回以降のブログで紹介するね。とりあえず今回は「余りが同じなんだな~」って思っておくだけでいいよ!
階乗(!)について
いきなり例で行くけど、$${5!=5\times4\times3\times2\times1=120}$$みたいな感じで$${1}$$づつ数字を減らした自然数を掛けたのを表してるよ。
だから$${13!=13\times12\times\cdots\times3\times2\times1=6227020800}$$みたいにすぐに数字は大きくなるよ!
これでさっきのウィルソンの定理の$${(p − 1)! ≡ −1 \pmod p}$$の意味は分かったんじゃないかな?
位数、原始根について
まず、$${r^{a}≡1\pmod m}$$となるような最小の$${a}$$を$${m}$$の位数って言って、特に$${a=p-1}$$のときの$${r}$$を$${m}$$の原始根っていうよ!
例えば、$${m=8}$$の時は$${3^2≡1\pmod 8}$$だから$${2}$$は位数だけど$${2≠8-1}$$だから$${3}$$は原始根じゃないね。
$${m=7}$$の時は、$${5^6≡1\pmod 7}$$だから$${6}$$は位数だし、$${7-1=6}$$だから$${5}$$は$${7}$$の原始根だよ。
原始根に関する定理がいくつかあって
定理1
任意の素数$${p}$$に対して原始根が存在する。
定理2
奇素数$${p}$$の原始根は$${1\sim p}$$の中に$${\varphi(p-1)}$$個存在する。
ここでの$${\varphi(m)}$$っていうのは$${m}$$を割り切らない自然数の個数を表してるよ。
定理3
素数$${p}$$に対する原始根$${r}$$とすると、$${1(=r^0),\ r,\ r^2,\dots,\ r^{p-1},\ r^{p-2}}$$を$${p}$$で割ったあまりはすべて異なり、$${1\sim p-1}$$を循環する。
この定理3はウィルソンの定理の証明に使うから覚えててね。
ここまでを踏まえて、
$${p}$$を素数とし、$${a}$$を$${p}$$の倍数でない整数とするとき、
$${a^{p-1}≡1\pmod p}$$
が成立する。
っていう定理をフェルマーの小定理っていうよ!
ウィルソンの定理の証明
ここからウィルソンの定理の証明が始まるよ!
証明
$${(p-1)!}$$
$${=(p-1)\times(p-2)\times\cdots\times3\times2\times1}$$
ここで$${p}$$の原始根を$${r}$$とし、定理3を使うと
$${≡r^0\times r^1\times r^2\times\cdots\times r^{p-3}\times r^{p-2}}$$
$${=r^{\frac{1}{2}(p-1)(p-2)}\pmod p}$$
となる。ここで、
$${r^{p-1}≡1\pmod p}$$
$${r^{p-1}-1≡0\pmod p}$$
$${(r^{\frac{p-1}{2}}+1)(r^{\frac{p-1}{2}}-1)≡0\pmod p}$$
であるから、$${r^{\frac{p-1}{2}}+1≡0\pmod p}$$か$${r^{\frac{p-1}{2}}-1≡0\pmod p}$$である。
$${r^{\frac{p-1}{2}}-1≡0\pmod p}$$より$${r^{\frac{p-1}{2}}≡1\pmod p}$$であるがこれは$${r}$$が原始根であることに反する。
よって$${r^{\frac{p-1}{2}}≡-1\pmod p}$$
ゆえに
$${r^{\frac{1}{2}(p-1)(p-2)}≡(-1)^{p-2}\pmod p}$$
$${p-2}$$は奇数なので$${(p − 1)! ≡ −1 \pmod p}$$■
こんな感じだけど、なんでこれに感動したのかというと、この証明をきっかけに位数とか原始根を理解できたし、その有用性もわかったからかな?どちらかといえば潜在意識的にめっちゃいい!って思った気がするけど(笑)
まとめ
ほかにも原始根を有効に使う方法があるかもしれないけどこの証明が分かりやすいんじゃないかな?
もしこれからほかにいい証明とかがあったら紹介していくかも!
最後に
マロ:こんな感じの証明だったんだけどどう?
ミケ:理解できたし、定理3を使ってるのがいいね!
マロ:そこも面白いよね!
マロ:次回からは合同式についてもっと深掘りするね!
ミケ:楽しみにしとく!
間違いやリクエスト、感想などがあったらコメントしてください!
マロが喜びます!
byマロ
この記事が気に入ったらサポートをしてみませんか?
