
結び目理論を簡単に①
飼い主が疲れて寝ている時、マロはいつもお気に入りの青い紐で遊んでいます。今日はそこにミケを誘っているようです。
「なんか紐絡まっちゃった。」
「本当にマロは紐で遊ぶのがへたくそだね(笑)ここをこうしてこうすれば……、できた!」
「さすがミケ! あ、そういえばついでにこの黒のひももほどいてくれない? この前遊んでたら絡まっちゃったんだよね」
「もぉー、しょうがないな。ここをこうすれば、ってあれ? なんでこれわっかに結んでるの?」
「さぁ? あそこで寝てる人がむすんだんじゃない?」
これは一人遊びが下手なマロが成し得たことですが、ここにはその事実を知っている猫はいません。
「あそこにも絡まってる紐あるじゃん(笑)どうせいつか頼まれるだろうし、今のうちにほどいてあげるよ」
「さすがミケ、やさっしぃー!」
「って、今度は何これ、円にできない輪っかみたいになっちゃった。」
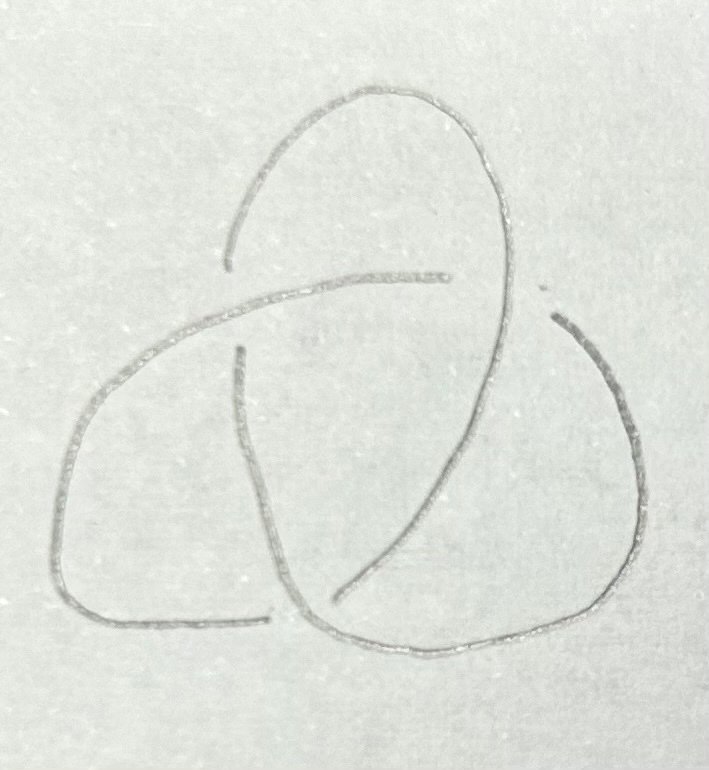
「お、それって三葉結び目じゃん!」
「ん? なにそれ?」
今回は結び目理論についてマロとミケは勉強していくみたいです。
結び目理論とは
結び目理論は、簡単に言うと、さっきミケががほどいた輪っかの紐を研究対象にしている理論です。
ここでいう結び目とは紐の輪っかのことを言います。
結び目の例
マロが絡めた紐のように、ミケがほどいていく過程で取り除くことができた交点を除去可能な交点または無駄な交点といい、これらをすべて取り除いた状態の結び目を分類します。
結び目にある紐と紐の交点の数を交点数と言い、以下で交点数が6以下の例と個数を紹介します。ただし、鏡像(鏡に映した姿)は数に含めていません。
交点数0
交点数0の結び目は1つあります。

上のような交点数0の結び目は自明な結び目という名前が付けられています。
また、この自明な結び目は、unknotと表します。
マロの黒い紐のように、無駄な交点を取り除いていった結果、自明な結び目となった結び目は解けていると言います。
交点数1
実は、交点数が1の結び目は存在しません。実際、交点数が1になりそうな紐を用意してみると、その唯一の交点は無駄な交点となっています。
交点数2
交点数が2の結び目も存在しません。これも同様に、交点数が2になりそうな紐を用意してみると、その2つの交点は無駄な交点となっています。
交点数3
交点数3の結び目は1つあります。

上のような交点数3の結び目は三葉結び目という名前が付けられています。先程マロが言っていたものですね。
また、この三葉結び目は、$${3_1}$$と表します。
交点数4
交点数4の結び目は1つあります。

上のような交点数4の結び目は8の字結び目という名前が付けられています。
また、8の字結び目は、$${4_1}$$と表します。
交点数5
交点数5の結び目は2つあります。

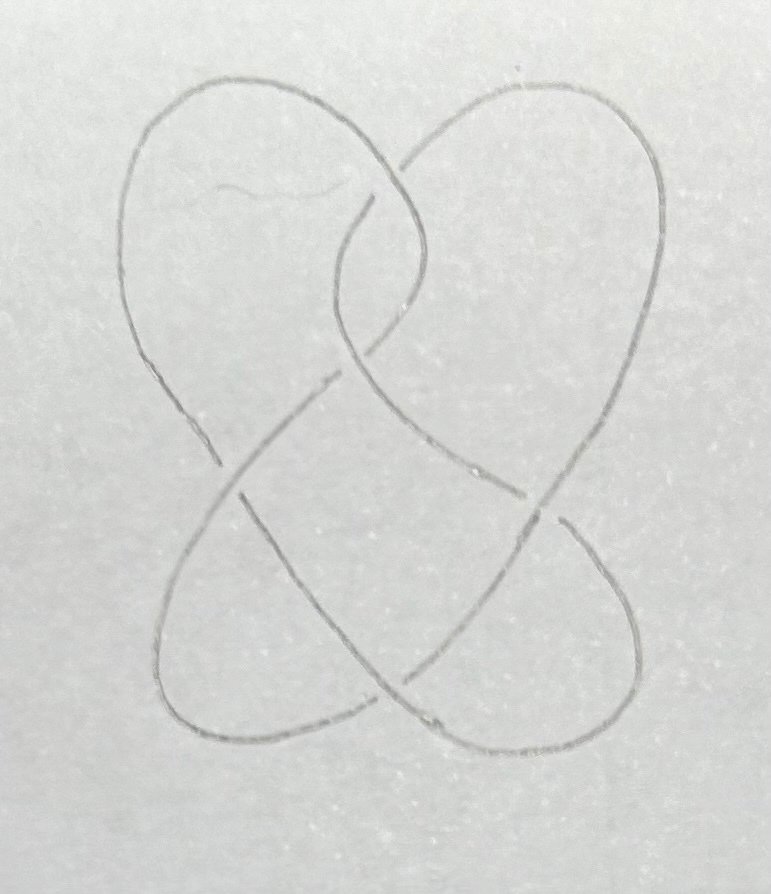
その1の結び目には五葉結び目という名前が付けられています。
また、これらは上から順に、$${5_1}$$、$${5_2}$$と表されます。
交点数6
交点数6の結び目は3つあります。



これらは上から順に、$${6_1}$$、$${6_2}$$、$${6_3}$$と表されます。
結び目の簡単な見分け方
複雑に絡み合ってる縄から無駄な交点を全て取り除き、交点数を調べるのはとても手間と時間がかかります。
そこで次のような結び目の判定方法があります。
アレクサンダー多項式
交点数が$${n}$$の結び目は、平面を$${n+2}$$個の領域に分割します。また、アレクサンダー多項式を求める前に結び目に向きを決めておきます。
そこで、まずは$${n\times (n+2)}$$の行列を作ります。行は交点に対応し、列は領域に対応します。
この行列の成分は次のように、交点と領域の関係によって決まります。
領域が交点をくぐる前の左側にあるとき、$${-t}$$
領域が交点をくぐる前の右側にあるとき、$${1}$$
領域が交点をくぐった後の左側にあるとき、$${t}$$
領域が交点をくぐった後の右側にあるとき、$${-1}$$
領域と交点が隣接していないとき、$${0}$$
こうしてできた行列は接続行列といいます。そして、接続行列から隣接する領域に対応する2つの列を取り除きます。隣接していればどの二つを選んでも構いません。こうしてできた$${n\times n}$$行列の行列式を計算できます。
こうして得られる$${t}$$の多項式がアレクサンダー多項式です。
しかし、取り除いた列によって行列式の値は$${\pm t^m(0\le m\le n)}$$を掛けた分だけ違ってきます。この差をなくすために、多項式の中で$${t}$$の最小の冪で多項式を割り、$${-1}$$を掛けたりして定数項が正になるようにします。
このアレクサンダー多項式はある結び目に対して固有のものです。ゆえに、一見三葉結び目に見えない紐があったとしても、無駄な交点を一個づつ取り除く過程は踏まないで三葉結び目と見抜くことができます。
ここからは、三葉結び目のアレクサンダー多項式を求めてみましょう。
まずは、次のように向きを決め、交点と領域に番号を振り分けます。

次に、接続行列を求めていきます。実際に求めると次のようになります。
$$
\begin{pmatrix}
-1 & -t & 0 & 1 & t \\
0 & -1 & -t & 1 & t \\
-t & 0 & -1 & 1 & t
\end{pmatrix}
$$
そして、隣接する領域に対応する2つの列を取り除き、$${n\times n}$$を作ります。今は3の領域と5の領域を取り除いてみましょう。
$$
\begin{pmatrix}
-1 & -t & 1 \\
0 & -1 & 1 \\
-t & 0 & 1
\end{pmatrix}
$$
そして、この行列式の値を求めればアレクサンダー多項式となります。実際に計算してみると、三葉結び目のアレクサンダー多項式は$${t^2-t+1}$$となります。
では、取り除く領域を1と4にして行列式を求めたらどうなるでしょうか。計算すると、$${t^3-t^2+t}$$となります。
事前の説明の通り、$${t}$$を掛けた分だけ違っています。では、$${t}$$で割って、定数項を正にしてみましょう。
$${t^2-t+1}$$となり、先程求めたアレクサンダー多項式と一致しましたね。
計算の手間としては、5の領域があると手間がかかります。そこで、接続行列を作る段階で5の領域とそれに隣接する領域を取り除いておきましょう。そうすれば時短になります。
では、次にこの紐のアレクサンダー多項式を求めてみてください。

計算すると、$${t^4-t^3+t^2}$$になったと思います。$${t^2}$$で割れば三葉結び目と同じ多項式ですね。ということは、この複雑そうに見えた紐は三葉結び目だったのです。
鏡像
三葉結び目は、自身を変形しても鏡像(鏡に映った姿)と同じ形にはなりません。
そこで、三葉結び目は右手型と左手型に分けられます。


この右手型と左手型は三葉結び目以外にも見られますが、例えば8の字結び目は自身と鏡像が一致します。このような結び目は両手型結び目と呼びます。自明な結び目も両手型結び目と呼べるでしょう。
また、ある結び目が両手型結び目なのか、そうではないのかはアレクサンダー方程式によって判定することができません。
そこで新たに、ジョーンズ多項式というものを使います。この多項式はマロの次回のお楽しみに。
まとめ
今回は結び目と、アレクサンダー多項式についてお話させていただきました。結び目理論についてはしっかり勉強できていなく、間違った説明をしているかもしれませんがご了承ください。いつかしっかり理解したうえでもっと深堀りした説明ができるように励んでまいります。
今回と次回の目的としては、結び目理論の理解を促すものというよりは結び目理論に踏み出すきっかけを作るというものです。もし興味を持っていただけたらぜひ、結び目理論の本を手に取って専門的に勉強してみてください。
最後に
「まさかマロが遊び下手なところからこんな話になるなんて……」
「これはマロが遊び上手だったからだよ!」
「いやいや、たまたまだからね?」
二匹で話していると、飼い主の目覚めの時間まであと少しとなっていました。勝手にミケを挙げてしまったマロはこのことがばれると怒られてしまいます。いそいでミケを見送ると、マロは再び一人遊びをし始めました。
