「微分とは傾きである 」を確認してみた

「微分の計算って、傾きを求めているんだよ」という話を聞いたことがある方は多いと思います。でも、傾きの計算と微分が同じものであることを確認する方法をはっきり示せる方は意外と少ないのではないでしょうか？

もちろん、数学を専門的に扱っている技術者はできて当たり前のことですが、一般の方々は自信ないと思う人も少なからずいると思います。

以前に書いた記事で、「微分とは傾きの計算のことです」ということを書いたことはありましたが、まだその検証はしておりませんでした。なので、今回、実際に検証していきます。

微分の定義式というのは、こんなやつです ↓

それに対して、傾きの計算というのは、こんな表現になります ↓

lim というのの意味は、ここに示したA点とB点の距離を、極限まで小さくしていったときということです。
この表現に至る詳細はこちらの記事をご覧ください！

（この時は f(x) ではなく、y で書いてますが、同じものです。）

で、微分の定義と傾きの式を見比べてみて、

「なるほど！おっしゃる通り、同じものですね (*´▽｀*)」

て、感じに腹落ちする人は、あまりいないのではないでしょうか。だって、全然形違いますもん。

同じだというなら、なにかしら式変形をしたら、全く同じ形にできるはずです。というわけで、傾きの計算を深掘りして、微分の定義式が作れることを示していきます。

傾きの計算を改めてひも解きます

以前の記事「微分とか何の意味あるん？（２）」で詳しく書いてますが、傾き計算の図解を改めて載せると ↓ のようなものでした。

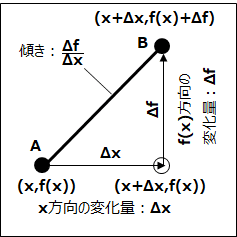
説明のしやすさのために、区間の両端の2点をA，B としました。点 A の座標は (x，f(x)) と設定すると、横にΔx、縦にΔf 増加した位置が点 B 。なので、B の座標は (x+Δx，f(x)+Δf) です。

ここからスタートして、本当に微分の定義式になるのか・・・、ゴールが見えない方もいるかもしれませんが、f(x) の表現方法に注目すれば、意外とすんなりいきます！

f(x)+Δf を書き換えれたら、ゴールはもう目の前

f(x) は、変数が x の時の f の値、ていう意味でした。変数が0だったら、f(0) と書くんでしたよね。そのことを考えると、変数が x+Δx の時の f は、図では f(x)+Δf と書きましたが、今のルールに倣えば、f(x+Δx) と書けます。
つまり、

です。

次に、傾きの計算である f(x)の変化量/xの変化量 のところに注目してみましょう。

x の変化量は、[Bの水平方向の位置]－[Aの水平方向の位置]＝(x+Δx)－x だから Δx とすぐわかります。（傾き計算の図解を見てください）

同じ考え方で f(x) の変化量を見ると、f(x)+Δf ＝ f(x+Δx) であることを考えれば、

[Bの垂直方向の位置]－[Aの垂直方向の位置]
＝ ( f(x)+Δf ) － f(x)
＝ f(x＋Δx) － f(x)

と書けます。これを踏まえて、傾きの計算式を見直すと、

もうお気づきですね。微分の定義式は ↓ でした。

まとめ

傾きの図解 ↓ からスタートして傾きの計算をしたら、

確かに微分の定義式と一致しました。

今回の記事、「微分とか何の意味あるん？」シリーズの（５）として、書いていたんですが、話題が計算の深いところに入ってきて、タイトルと内容が一致しない問題が出てきてしまいました。

なので、思い切ってタイトルを変えての投稿としてみました。noteで記事を書き始めて１ヶ月くらい経ちましたが、読まれる記事を書くというのは・・・難しいですね。

まだまだ勉強と訓練が必要だと感じてます。

「微分とか何の意味あるん？」シリーズの（１）は ↓ です。

気になったら、ぜひクリックしてみてください！