微分とか何の意味あるん？（２）

高校数学で習う微分。何の意味があるのかというテーマの2回目です。1回目をお読みでない方はぜひ↓をクリックください。

前回は、微分の計算というものをただ機械的にやりましたが、今回は、その微分の計算は一体何のための計算なのか、というところを掘り下げていこうと思います。

一言でいうと、微分というのは傾きを計算する手法です。そこで、傾きとは何かを簡単におさらいしつつ、前回の計算がなぜ傾きの計算をしたことになるのか、つまり、微分の計算はなぜ傾きの計算になるのか、というところを書いていきます！

傾きとは何か

簡単な図で書くならこんな感じでしょうか。

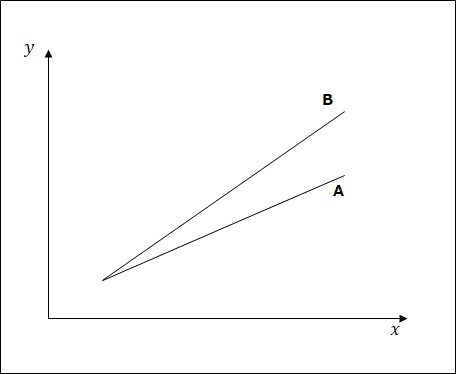
AとBと名付けられた線がありますが、見た目からBは傾いてますね。Aは水平なので傾いてない。数学の表現をするならAは傾き0となります。これだけだと傾いてるか、傾いてないかの話で終わってしまうので、もう少し話を掘り下げます。

傾きの大小

こんどはAとBのどちらも傾いてますが、見た目的にBの方が傾いているといえそうです。例えば、xとyの値が、下の図のようになっていた場合、

数学ではAとBの傾きを↓のように計算します。

端的に言うと、Bの計算結果の方が大きいからBの方が傾きが大きいということになります。どういう計算をしているかというと、xが3から9まで増える間にyがどれだけ増えているかを傾きと定義しています。

一般論でまとめるとxy座標の線における傾きというのは、下のような計算をします。（Δは「デルタ」と読みます。一般に変化量を表すときに使う記号です。）

傾きを求める対象が直線の時なら、上の計算方法で傾きの計算は完璧です。でも、対象が曲線だったらどうなるでしょうか。例えば下の図。

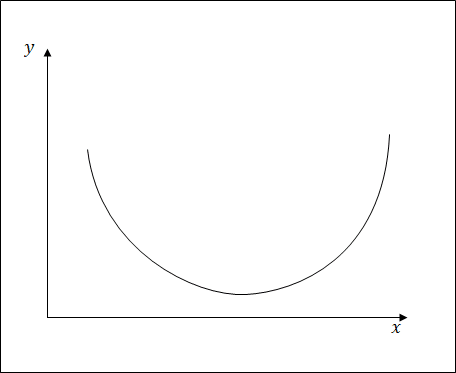
左の方は右肩下がりだし、右の方は右肩上がりだし、場所によって傾き方が変わります。こういう場合、どうすれば傾きを計算できるでしょうか。

とりあえずできるところから始めてみましょう。曲線状にAとBの2点をセットし、2点間を結ぶ線分の傾きというものを考えてみます。

この線分の傾きというのは曲線状のAの位置の傾きとも、Bの位置の傾きとも別物ですが、曲線状のAからBの区間の平均の傾きを表していると解釈することはできます。

もし、点Aの傾きを求めたいと考えているとき、Bとの区間を狭めてやると・・・、

みた感じ、AとBを結ぶ線の傾きはさっきよりAの傾きに近づいた気がしますね。それなら、BをもっともっとAに近づけていけば、よりAの傾きに近づくような気がします。究極的にはこんな感じです。

実は、この考え方こそが微分の本質です。前の図にあった点BがAに近づき、両者の距離が0になったと思ってください。

この考え方を傾きの式で表現すると↓のようになります。

limという記号が出てきましたが引かないでください。下に書いてある「○○→0」というのがありますが、「○○が0に近づいた時を想定する」という記号です。

つまり、「ある区間」がどんどん狭くなり、区間距離が0になったということ、一番右の＝の式でいうならxの変化量Δxが限りなく0に近づいたことを想定したときの計算という意味です。

今回のまとめ

今回は、微分がやろうとしていることは、傾きの計算なのだ、ということを説明してみました。二つの点を結ぶ線分の傾きを求める時、二点の距離を極限まで近づけて計算すると微分になる。ということが今回書きたかった内容です。

前回記事「微分とか何の意味あるん？（１）」で機械的に計算した内容と、今回の傾きを求める話は、どちらも微分なんで、同じことをしていることになります。

でも、多分そのことがしっくり理解できない方も少なからずいると思います。次回は、（１）で用いた、y=ax2+bx+cという式の傾きを求めることを通して、前回記事と今回時期の内容が同じことであるということを示していこうと思います。

この記事の上位テーマは ↓ です。よかったらアクセスしてみてください。